算法篇【递归2 -- N皇后问题】

问题：输入整数N，要求在N*N的棋盘上，互相不能攻击，不在同一行同一列上，切不在对角线上，输出全部方案。

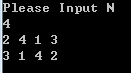
输入：

4

输出：

2  4  1  3

3  1  4  2

思路：

假设在前k-1个摆好的条件下，求出第k个皇后的摆法，并保存，继续求第k+1个皇后的摆法，直到找到合适的摆法。

 #include <iostream>
 #include <cmath>
 using namespace std;
 int  N ;
 int  queenPos[] ;
 //用来存放算好的皇后的位置，比如第1行皇后在第i列，则queenPos[0]=i; 第2行皇后在第j列，则queenPos[1]=j;依次输出所有n行皇后的位置
 void NQueen(int k);
 //NQueen(k) 表示前k-1个皇后都摆好的情况下，第k个皇后的摆法。

 int main(){
     cout << "Please Input N " << endl;
     cin >> N  ;
     NQueen() ;//从第0行开始摆皇后 ，直到摆好N行
     return   ;
     system("pause");
 }

 void NQueen(int k){
     int  i ;
     if(k==N){
         //递归函数的结束条件。从第1个皇后到第N个皇后都已经摆好了
         for(int i=; i<N; i++){
             cout << queenPos[i] +  << " ";
         }
         cout << endl;
         return ;
     }

     //该for循环用来尝试第k个皇后的位置 ，位置为变量i
     for(int i=; i<N; i++){
         int j ;
         //变量j的循环用来判断第k个皇后放在位置i列处，是否和已经摆好的k-1个皇后的列位置queenPos[j]冲突
         for(j=; j<k; j++){
             if(queenPos[j] == i ||//第k个皇后摆在第i列和已经摆放的皇后列位置有相同的。
                 abs(queenPos[j]-i) == abs(k-j)//列的绝对值只差==行的绝对值只差，k-j中的k表示第k个皇后在第k行，循环变量j表示的是已经摆好的行数下标。
               )
                 break ;
         }
         if(j==k){//前面j的for循环没有break，则表示当前第k行的位置i不冲突，则保存该值，并在此基础上求下一行皇后的摆放位置
             queenPos[k] = i;
             NQueen(k+);//首先会判断新的k是否==N，是的话，则输出摆放位置 ，return到NQueen[N-1],...直到返回NQueen【0】，main函数执行return 0.
         }
     }
     //假设N=4，由于求NQueen（0）时，第一个皇后的位置是2，此时在for（int i=0; i<N; i++）。的循环中，成功return 之后返回到for 循环中，重新计算出下一个合理摆法
 }