HDU 2894 DeBruijin (数位欧拉)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2894

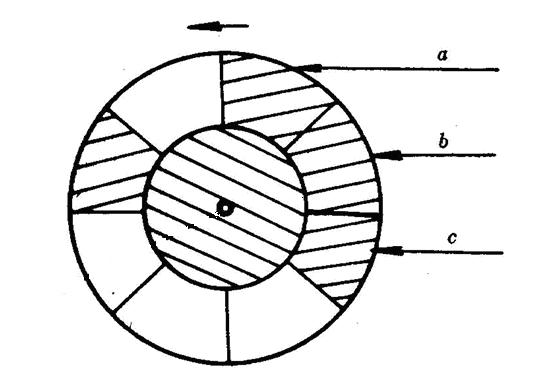
题目大意：旋转鼓的表面分成m块扇形,如图所示(m=8)。图中阴影区表示用导电材料制成,空白区用绝缘材料制成,终端a、b和c是3（k=3）处接地或不是接地分别用二进制信号0或1表示。因此,鼓的位置可用二进制信号表示。试问应如何选取这8个扇形的材料使每转过一个扇形都得到一个不同的二进制信号,即每转一周,能得到000到111的8个数。

那我们现在把旋转鼓的表面分成m块扇形，每一份记为0或1，使得任何相继的k个数的有序组（按同一方向）都不同，对固定的k，m最大可达到多少，并任意输出符合条件的一个这样的有序组。

Input

每个case输入一个数k （2<=k<=11）,表示图中所示的abc这样的接地线的数量。

Output

每个case输出m所能达到的最大值 ，并且输出字典序最小的一个符合条件的有序组，中间用空格隔开。Case间没有空行。有序组输出的格式为：00010111（k=3，只输出一个周期（0001011100010111……），并且首尾刚好是相接的）。

解题思路：参考链接

第一问m达到的最大值为2^k。

第二问就是模拟一下旋转鼓接地线的旋转过程，每次旋转即删去第一个数，然后在最后加一个0(a<<1&((1<<k)-1))或1(a<<1&((1<<k)-1)+1)，同时标记出现过的数字，保证每个出现的数字都不同。

因为所有数为0到2^k-1，对于任意给定的点a，将它与点a1=a<<1&((1<<k)-1)与点a2=a1+1分别连一条边，构成欧拉回路（每个点入度=出度=2），加一个vis数组确定每个数出现一次。因为结果需要按照字典序从小到大排，所以首先输出的必然是k个前导0，然后dfs判断0或1时先判0，再判1，逆序输出即可（dfs回溯）。

代码：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define CLR(arr,val) memset(arr,val,sizeof(arr))
 using namespace std;
 const int N=;

 int k,cnt;
 int ans[<<N];
 bool vis[<<N];

 void init(){
     CLR(vis,false);
     CLR(ans,);
     cnt=;
 }

 void euler(int st) {
     int s1=(st<<)&((<<k)-);
     int s2=s1+;
     if (!vis[s1]){
         vis[s1]=;
         euler(s1);
         ans[++cnt]=;
     }
     if (!vis[s2]) {
         vis[s2]=;
         euler(s2);
         ans[++cnt]=;
     }
 }

 int main(){
     while(~scanf("%d",&k)){
         init();
         euler();
         printf("%d ",cnt);
         //因为要求字典序最小,所以前k位都是0（前导零）
         for(int i=;i<k;i++){
             printf("");
         }
         for(int i=cnt;i>=k;i--){
             printf("%d",ans[i]);
         }
         printf("\n");
     }
     return ;
 }