29-中国剩余定理CRT
中国剩余定理的具体描述是这样的:

给出你n个ai和mi,最后让求出x的最小值是多少。
中国剩余定理说明:假设整数m1, m2, ... , mn两两互质,则对任意的整数:a1, a2, ... , an,方程组 有解,并且通解可以用如下方式构造得到:
有解,并且通解可以用如下方式构造得到:
- 设
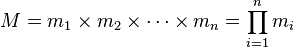 是整数m1, m2, ... , mn的乘积,并设
是整数m1, m2, ... , mn的乘积,并设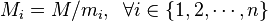 是除了mi以外的n - 1个整数的乘积。
是除了mi以外的n - 1个整数的乘积。 - 设
 为
为 模
模 的数论倒数:
的数论倒数:
- 方程组
 的通解形式为:
的通解形式为: 在模
在模 的意义下,方程组
的意义下,方程组 只有一个解:
只有一个解: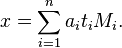
使用中国剩余定理来求解上面的“物不知数”问题,便可以理解《孙子歌诀》中的数字含义。这里的线性同余方程组是:
三个模数m1 3, m2
3, m2 5, m3
5, m3 7的乘积是M
7的乘积是M 105,对应的M1
105,对应的M1 35, M2
35, M2 21, M3
21, M3 15. 而可以计算出相应的数论倒数:t1
15. 而可以计算出相应的数论倒数:t1 2, t2
2, t2 1, t3
1, t3 1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:
1. 所以《孙子歌诀》中的70,21和15其实是这个“物不知数”问题的基础解:
而将原方程组中的余数相应地乘到这三个基础解上,再加起来,其和就是原方程组的解:
这个和是233,实际上原方程组的通解公式为:
《孙子算经》中实际上给出了最小正整数解,也就是k -2时的解:x
-2时的解:x 23.
23.
- ///n个mi互质
- const LL maxn = 20;
- LL a[maxn], m[maxn], n;
- LL CRT(LL a[], LL m[], LL n)
- {
- LL M = 1;
- for (int i = 0; i < n; i++) M *= m[i];
- LL ret = 0;
- for (int i = 0; i < n; i++)
- {
- LL x, y;
- LL tm = M / m[i];
- ex_gcd(tm, m[i], x, y);
- ret = (ret + tm * x * a[i]) % M;
- }
- return (ret + M) % M;
- }
分割线
- ///n个mi不互质
- const LL maxn = 1000;
- LL a[maxn], m[maxn], n;
- LL CRT(LL a[], LL m[], LL n) {
- if (n == 1) {
- if (m[0] > a[0]) return a[0];
- else return -1;
- }
- LL x, y, d;
- for (int i = 1; i < n; i++) {
- if (m[i] <= a[i]) return -1;
- d = ex_gcd(m[0], m[i], x, y);
- if ((a[i] - a[0]) % d != 0) return -1; //不能整除则无解
- LL t = m[i] / d;
- x = ((a[i] - a[0]) / d * x % t + t) % t; //第0个与第i个模线性方程的特解
- a[0] = x * m[0] + a[0];
- m[0] = m[0] * m[i] / d;
- a[0] = (a[0] % m[0] + m[0]) % m[0];
- }
- return a[0];
- }
以上大部分内容来自wiki
29-中国剩余定理CRT的更多相关文章
- 「中国剩余定理CRT」学习笔记
设正整数$m_1, m_2, ... , m_r$两两互素,对于同余方程组 $x ≡ a_1 \ (mod \ m_1)$ $x ≡ a_2 \ (mod \ m_2)$ $...$ $x ≡ a_r ...
- 中国剩余定理CRT(孙子定理)
中国剩余定理 给出以下的一元线性同余方程组: $\Large(s):\left\{\begin{aligned}x\equiv a_1\ (mod\ m_1)\\x\equiv a_2\ (mod\ ...
- 【bzoj3782】上学路线 dp+容斥原理+Lucas定理+中国剩余定理
题目描述 小C所在的城市的道路构成了一个方形网格,它的西南角为(0,0),东北角为(N,M).小C家住在西南角,学校在东北角.现在有T个路口进行施工,小C不能通过这些路口.小C喜欢走最短的路径到达目的 ...
- acm数论之旅--中国剩余定理
ACM数论之旅9---中国剩余定理(CRT)(壮哉我大中华╰(*°▽°*)╯) 中国剩余定理,又名孙子定理o(*≧▽≦)ツ 能求解什么问题呢? 问题: 一堆物品 3个3个分剩2个 5个5个分剩3个 ...
- 卢卡斯定理&&中国剩余定理
卢卡斯定理(模数较小,且是质数) 式子C(m,n)=C(m/p,n/p)*C(m%p,n%p)%p 至于证明(我也不会QAQ,只要记住公式也该就好了). 同时卢卡斯定理一般用于组合数取模上 1.首先当 ...
- gcd,扩展欧几里得,中国剩余定理
1.gcd: int gcd(int a,int b){ ?a:gcd(b,a%b); } 2.中国剩余定理: 题目:学生A依次给n个整数a[],学生B相应给n个正整数m[]且两两互素,老师提出问题: ...
- NOI 2018 屠龙勇士 (拓展中国剩余定理excrt+拓展欧几里得exgcd)
题目大意:略 真是一波三折的一道国赛题,先学了中国剩余定理,勉强看懂了模板然后写的这道题 把取出的宝剑攻击力设为T,可得Ti*x=ai(mod pi),这显然是ax=c(mod b)的形式 这部分用e ...
- POJ 1006:Biorhythms 中国剩余定理
Biorhythms Time Limit: 1000MS Memory Limit: 10000K Total Submissions: 121194 Accepted: 38157 Des ...
- RSA遇上中国剩余定理
1.Introduction 最近读论文刚好用到了这个,之前只是有耳闻,没有仔细研究过,这里就好好捋一下,会逐步完善 不过貌似CRT(中国剩余定理)的实现更容易被攻击 2. RSA: Overview ...
- 《孙子算经》之"物不知数"题:中国剩余定理
1.<孙子算经>之"物不知数"题 今有物不知其数,三三数之剩二,五五数之剩七,七七数之剩二,问物几何? 2.中国剩余定理 定义: 设 a,b,m 都是整数. 如果 m ...
随机推荐
- RK3288 增加双屏异显 eDP+LVDS
CPU:RK3288 系统:Android 5.1 下面是官方文档中的信息. 1.rk3288 支持的显示接口可以任意组合. 2.双屏异显时,一个显示接口当主屏,另一个当副屏:主副屏由板级 dts 文 ...
- 常见企业IT支撑【7、keepalived VRRP双主master】
我们知道,最简单的keepalive vrrp作出来的VIP实例,征用了2台服务器,生成1个VIP,也就是说,基础实配置实例中,我们的业务流量只会流向其中一台服务器,另一台就空闲了,明显示合, 能否做 ...
- MOSS 2013研究系列---隐藏Ribbon
我们在开发Sharepoint 2013 的时候,常常需要隐藏Ribbon,那个Ribbon是属于Office的特征,但是我们做门户的时候,大家都不希望看见到它,但是我们又离不开它,以管理的身份进行设 ...
- javascript基础-js函数
一.创建函数的方式 1)普通方式 function cal( num1, num2 ) { return num1+num2; } 2)使用变量初始化方式 var plus = function(nu ...
- (转)jdbc 调用 sql server 的存储过程时“该语句没有返回结果集”的解决方法
本文转载自:http://hedyn.iteye.com/blog/856040 在JDBC中调用SQL Server中的存储过程时出现如下异常: com.microsoft.sqlserver.jd ...
- java代码---------陈勇老师的
总结:看看写的多漂亮啊 package com.test4; import java.awt.*; import java.awt.event.*; import javax.swing.*; pub ...
- java代码-----运用endWith()和start()方法
总结: package com.a.b; //startWith().和endWith()是检查一个字符串是否以一个特定的字符序列开始或结束 public class Sdfs { public st ...
- Java - 将 List 等分(最后一部分处理多余部分)
背景 今天由于要使用多线程,所以事先需要确定启动线程个数.于是需要先将集合进行分配,确定线程的个数. 解决方案 首先是实现 public static <T> List<List&l ...
- node中的ajax提交小例子
我们看一个HTML5页面中通过AJAX请求的方式获取HTTP服务器返回数据的代码示例.由于我们把服务器的端口指定为1337,并将从端口为80的网站中运行HTML5页面,因此这是一种跨域操作,需要在HT ...
- python学习笔记(十四): unittest
Python中有一个自带的单元测试框架是unittest模块,用它来做单元测试,它里面封装好了一些校验返回的结果方法和一些用例执行前的初始化操作. 在说unittest之前,先说几个概念: TestC ...



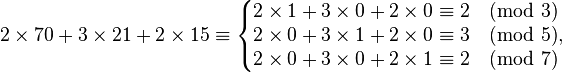

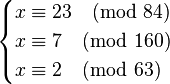 与
与 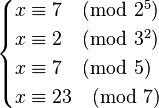 同解。
同解。