0xGame 2023【WEEK4】Crypto WP

Danger Leak

查看代码

from random import *
from secret import flag
from Crypto.Util.number import *

m = bytes_to_long(flag)
p = getPrime(1024)
q = getPrime(1024)
n = p * q
phi = (p - 1) * (q - 1)
while True:
    M = getrandbits(954)
    d0 = getrandbits(70)
    d1 = getrandbits(60)
    d = M * d1 + d0
    e = inverse(d, (p - 1) * (q - 1))
    if GCD(d,phi) == 1:
    	break

c = pow(m,e,n)
print(f'n = {n}')
print(f'e = {e}', )
print(f'c = {c}')
print(f'leak={M}')

'''
n = 20890649807098098590988367504589884104169882461137822700915421138825243082401073285651688396365119177048314378342335630003758801918471770067256781032441408755600222443136442802834673033726750262792591713729454359321085776245901507024843351032181392621160709321235730377105858928038429561563451212831555362084799868396816620900530821649927143675042508754145300235707164480595867159183020730488244523890377494200551982732673420463610420046405496222143863293721127847196315699011480407859245602878759192763358027712666490436877309958694930300881154144262012786388678170041827603485103596258722151867033618346180314221757
e = 18495624691004329345494739768139119654869294781001439503228375675656780205533832088551925603457913375965236666248560110824522816405784593622489392063569693980307711273262046178522155150057918004670062638133229511441378857067441808814663979656329118576174389773223672078570346056569568769586136333878585184495900769610485682523713035338815180355226296627023856218662677851691200400870086661825318662718172322697239597148304400050201201957491047654347222946693457784950694119128957010938708457194638164370689969395914866589468077447411160531995194740413950928085824985317114393591961698215667749937880023984967171867149
c = 7268748311489430996649583334296342239120976535969890151640528281264037345919563247744198340847622671332165540273927079037288463501586895675652397791211130033797562320858177249657627485568147343368981852295435358970875375601525013288259717232106253656041724174637307915021524904526849025976062174351360431089505898256673035060020871892556020429754849084448428394307414301376699983203262072041951835713075509402291301281337658567437075609144913905526625759374465018684092236818174282777215336979886495053619105951835282087487201593981164477120073864259644978940192351781270609702595767362731320959397657161384681459323
leak=136607909840146555806361156873618892240715868885574369629522914036807393164542930308166609104735002945881388216362007941213298888307579692272865700211608126496105057113506756857793463197250909161173116422723246662094695586716106972298428164926993995948528941241037242367190042120886133717
'''

参考论文：https://eprint.iacr.org/2014/035.pdf

可知在模Me的域中构造多项式：

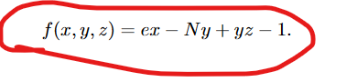
然后用多元copper解出根。

而 x₀, y₀, z₀ 分别对应 d₀, k, (p + q - 1)

故用多元copper求解的时候，以 d₀, k, (p + q - 1) 作为 x, y, z 的上限求得 (p + q - 1) 后，联立方程 n = p * q 即可解得p,q

即 p = (p + q) + ((p + q)² - 4n)^1/2 / 2

exp:

#sage
import hashlib
import itertools

N = 20890649807098098590988367504589884104169882461137822700915421138825243082401073285651688396365119177048314378342335630003758801918471770067256781032441408755600222443136442802834673033726750262792591713729454359321085776245901507024843351032181392621160709321235730377105858928038429561563451212831555362084799868396816620900530821649927143675042508754145300235707164480595867159183020730488244523890377494200551982732673420463610420046405496222143863293721127847196315699011480407859245602878759192763358027712666490436877309958694930300881154144262012786388678170041827603485103596258722151867033618346180314221757
e = 18495624691004329345494739768139119654869294781001439503228375675656780205533832088551925603457913375965236666248560110824522816405784593622489392063569693980307711273262046178522155150057918004670062638133229511441378857067441808814663979656329118576174389773223672078570346056569568769586136333878585184495900769610485682523713035338815180355226296627023856218662677851691200400870086661825318662718172322697239597148304400050201201957491047654347222946693457784950694119128957010938708457194638164370689969395914866589468077447411160531995194740413950928085824985317114393591961698215667749937880023984967171867149
c = 7268748311489430996649583334296342239120976535969890151640528281264037345919563247744198340847622671332165540273927079037288463501586895675652397791211130033797562320858177249657627485568147343368981852295435358970875375601525013288259717232106253656041724174637307915021524904526849025976062174351360431089505898256673035060020871892556020429754849084448428394307414301376699983203262072041951835713075509402291301281337658567437075609144913905526625759374465018684092236818174282777215336979886495053619105951835282087487201593981164477120073864259644978940192351781270609702595767362731320959397657161384681459323
M = 136607909840146555806361156873618892240715868885574369629522914036807393164542930308166609104735002945881388216362007941213298888307579692272865700211608126496105057113506756857793463197250909161173116422723246662094695586716106972298428164926993995948528941241037242367190042120886133717

def small_roots(f, bounds, m=1, d=None):
    if not d:
        d = f.degree()

    R = f.base_ring()
    N = R.cardinality()

    f /= f.coefficients().pop(0)
    f = f.change_ring(ZZ)

    G = Sequence([], f.parent())
    for i in range(m + 1):
        base = N ^ (m - i) * f ^ i
        for shifts in itertools.product(range(d), repeat=f.nvariables()):
            g = base * prod(map(power, f.variables(), shifts))
            G.append(g)

    B, monomials = G.coefficient_matrix()
    monomials = vector(monomials)

    factors = [monomial(*bounds) for monomial in monomials]
    for i, factor in enumerate(factors):
        B.rescale_col(i, factor)

    B = B.dense_matrix().LLL()

    B = B.change_ring(QQ)
    for i, factor in enumerate(factors):
        B.rescale_col(i, 1 / factor)

    H = Sequence([], f.parent().change_ring(QQ))
    for h in filter(None, B * monomials):
        H.append(h)
        I = H.ideal()
        if I.dimension() == -1:
            H.pop()
        elif I.dimension() == 0:
            roots = []
            for root in I.variety(ring=ZZ):
                root = tuple(R(root[var]) for var in f.variables())
                roots.append(root)
            return roots

    return []

R.<x,y,z>=PolynomialRing(Zmod(M*e))

f = e*x - N*y + y*z - 1
solves = small_roots(f,bounds=(2^71,2^1013,2^1026),m=3, d=3) #m从1试到了3,d = 3表示变量个数
print(solves)

add = int(solves[0][2]) + 1                # p+q
sub = gmpy2.iroot(add^2 - 4*N,2)[0]        # p-q
p = (add + sub)//2
q = N//p

print(p)
print(q)
#p = 159187299445690865936209866231455891490202310744152845744977069391022410393468912328412844430232217990368102754558794976071725279063674210377065270563586203180456906628982612217129511798538144544958405844931094861006397389031757152191477500599686769201220015540331289069913036482174254767875156584338903962407
#q = 131233144100326025114495160232596252620839837217325176787017551336602642561585505042021917030847824474637871880118433653215132173184171592169587459092564461899213639155235907204204645743042085695224470680284778641807140287858947264311083089482674209055540250410763250174232527931696033122830989835732192477051

from Crypto.Util.number import *
import gmpy2

N = 20890649807098098590988367504589884104169882461137822700915421138825243082401073285651688396365119177048314378342335630003758801918471770067256781032441408755600222443136442802834673033726750262792591713729454359321085776245901507024843351032181392621160709321235730377105858928038429561563451212831555362084799868396816620900530821649927143675042508754145300235707164480595867159183020730488244523890377494200551982732673420463610420046405496222143863293721127847196315699011480407859245602878759192763358027712666490436877309958694930300881154144262012786388678170041827603485103596258722151867033618346180314221757
e = 18495624691004329345494739768139119654869294781001439503228375675656780205533832088551925603457913375965236666248560110824522816405784593622489392063569693980307711273262046178522155150057918004670062638133229511441378857067441808814663979656329118576174389773223672078570346056569568769586136333878585184495900769610485682523713035338815180355226296627023856218662677851691200400870086661825318662718172322697239597148304400050201201957491047654347222946693457784950694119128957010938708457194638164370689969395914866589468077447411160531995194740413950928085824985317114393591961698215667749937880023984967171867149
c = 7268748311489430996649583334296342239120976535969890151640528281264037345919563247744198340847622671332165540273927079037288463501586895675652397791211130033797562320858177249657627485568147343368981852295435358970875375601525013288259717232106253656041724174637307915021524904526849025976062174351360431089505898256673035060020871892556020429754849084448428394307414301376699983203262072041951835713075509402291301281337658567437075609144913905526625759374465018684092236818174282777215336979886495053619105951835282087487201593981164477120073864259644978940192351781270609702595767362731320959397657161384681459323
p = 159187299445690865936209866231455891490202310744152845744977069391022410393468912328412844430232217990368102754558794976071725279063674210377065270563586203180456906628982612217129511798538144544958405844931094861006397389031757152191477500599686769201220015540331289069913036482174254767875156584338903962407
q = 131233144100326025114495160232596252620839837217325176787017551336602642561585505042021917030847824474637871880118433653215132173184171592169587459092564461899213639155235907204204645743042085695224470680284778641807140287858947264311083089482674209055540250410763250174232527931696033122830989835732192477051

d = gmpy2.invert(e,(p-1)*(q-1))
m = pow(c,d,N)
print(long_to_bytes(int(m)))
# 0xGame{a9e1f260f845be84f56ff06b165deb80}

经过多次测试发现，k大概在1013bit以下,而(p + q - 1)的大小在1025bit左右，故bound设置为(2^71,2^1013,2^1026)

Normal ECC

1、题目信息

Hint 1: assert E.order() == p

查看代码

from Crypto.Util.number import getPrime
from Crypto.Cipher import AES
from random import getrandbits
from hashlib import md5
from secret import flag,M

def MD5(m):return md5(str(m).encode()).hexdigest()
assert '0xGame{'+MD5(M[0])+'}' == flag
p = 11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
a = 490963434153515882934487973185142842357175523008183292296815140698999054658777820556076794490414610737654365807063916602037816955706321036900113929329671
b = 7668542654793784988436499086739239442915170287346121645884096222948338279165302213440060079141960679678526016348025029558335977042712382611197995002316466
assert p>a
assert p>b
E = EllipticCurve(GF(p),[a,b])
assert E.order() == p
M = E(M)

G = E.random_point()
k = getPrime(int(128))
K = k*G
r = getrandbits(64)

C1 = M + r*K
C2 = r*G

print(f'p={p}\na={a}\nb={b}')
print(f'G={G.xy()}')
print(f'K={K.xy()}')
print(f'C1={C1.xy()}')
print(f'C2={C2.xy()}')

'''
p=11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
a=490963434153515882934487973185142842357175523008183292296815140698999054658777820556076794490414610737654365807063916602037816955706321036900113929329671
b=7668542654793784988436499086739239442915170287346121645884096222948338279165302213440060079141960679678526016348025029558335977042712382611197995002316466
G=(4045939664332192284605924284905750194599514115248885617006435833400516258314135019849306107002566248677228498859069119557284134574413164612914441502516162, 2847794627838984866808853730797794758944159239755903652092146137932959816137006954045318821531984715562135134681256836794735388745354065994745661832926404)
K=(9857925495630886472871072848615069766635115253576843197716242339068269151167072057478472997523547299286363591371734837904400286993818976404285783613138603, 9981865329938877904579306200429599690480093951555010258809210740458120586507638100468722807717390033784290215217185921690103757911870933497240578867679716)
C1=(4349662787973529188741615503085571493571434812105745603868205005885464592782536198234863020839759214118594741734453731681116610298272107088387481605173124, 10835708302355425798729392993451337162773253000440566333611610633234929294159743316615308778168947697567386109223430056006489876900001115634567822674333770)
C2=(5193866657417498376737132473732737330916570240569047910293144235752602489388092937375844109374780050061859498276712695321973801207620914447727053101524592, 684299154840371832195648774293174908478389728255128448106858267664482339440737099810868633906297465450436417091302739473407943955874648486647511119341978)
'''

关于椭圆曲线减法的题，题目给了一条曲线，基点G，K = r*G 其中r未知并给出C1 = M + r*K ;C2 = r*G，提示E.order()==p。

发现曲线的阶和p一样，用SmartAttack求出r，从C2和G可以求出r，然后得到r*K，不过这有个坑，对于阿贝尔群C = A+B不能直接用C-A来求B,需要C+(-A)这个-A就是A点对x轴的对称点也就是y取反。

exp:

from hashlib import md5

p=11093300438765357787693823122068501933326829181518693650897090781749379503427651954028543076247583697669597230934286751428880673539155279232304301123931419
a=490963434153515882934487973185142842357175523008183292296815140698999054658777820556076794490414610737654365807063916602037816955706321036900113929329671
b=7668542654793784988436499086739239442915170287346121645884096222948338279165302213440060079141960679678526016348025029558335977042712382611197995002316466

G=(4045939664332192284605924284905750194599514115248885617006435833400516258314135019849306107002566248677228498859069119557284134574413164612914441502516162, 2847794627838984866808853730797794758944159239755903652092146137932959816137006954045318821531984715562135134681256836794735388745354065994745661832926404)
K=(9857925495630886472871072848615069766635115253576843197716242339068269151167072057478472997523547299286363591371734837904400286993818976404285783613138603, 9981865329938877904579306200429599690480093951555010258809210740458120586507638100468722807717390033784290215217185921690103757911870933497240578867679716)
C1=(4349662787973529188741615503085571493571434812105745603868205005885464592782536198234863020839759214118594741734453731681116610298272107088387481605173124, 10835708302355425798729392993451337162773253000440566333611610633234929294159743316615308778168947697567386109223430056006489876900001115634567822674333770)
C2=(5193866657417498376737132473732737330916570240569047910293144235752602489388092937375844109374780050061859498276712695321973801207620914447727053101524592, 684299154840371832195648774293174908478389728255128448106858267664482339440737099810868633906297465450436417091302739473407943955874648486647511119341978)

E = EllipticCurve(GF(p),[a,b])
G = E(G)
K = E(K)
C1 = E(C1)
C2 = E(C2)

order = E.order()
print(order)
print(order == p)
def MD5(m):return md5(str(m).encode()).hexdigest()

def SmartAttack(P,Q,p):
    E = P.curve()
    Eqp = EllipticCurve(Qp(p, 2), [ ZZ(t) + randint(0,p)*p for t in E.a_invariants() ])

    P_Qps = Eqp.lift_x(ZZ(P.xy()[0]), all=True)
    for P_Qp in P_Qps:
        if GF(p)(P_Qp.xy()[1]) == P.xy()[1]:
            break

    Q_Qps = Eqp.lift_x(ZZ(Q.xy()[0]), all=True)
    for Q_Qp in Q_Qps:
        if GF(p)(Q_Qp.xy()[1]) == Q.xy()[1]:
            break

    p_times_P = p*P_Qp
    p_times_Q = p*Q_Qp

    x_P,y_P = p_times_P.xy()
    x_Q,y_Q = p_times_Q.xy()

    phi_P = -(x_P/y_P)
    phi_Q = -(x_Q/y_Q)
    k = phi_Q/phi_P
    return ZZ(k)

r = SmartAttack(G,C2,p)
print(r)

M = C1 - r*K
flag = '0xGame{'+MD5(M[0])+'}'
print(flag)
# 0xGame{6f2b3accf11a8cb7a9d3c7b159bc6c6c}