数据分析（以kaggle上的加州房价为例）

数据来源：House Prices - Advanced Regression Techniques

参考文献：

• Comprehensive data exploration with Python

1. 导入数据

import pandas as pd
import warnings
warnings.filterwarnings('ignore') # 忽略警告

df_train = pd.read_csv('./house-prices-advanced-regression-techniques/train.csv')

df_train.columns

Index(['Id', 'MSSubClass', 'MSZoning', 'LotFrontage', 'LotArea', 'Street',
       'Alley', 'LotShape', 'LandContour', 'Utilities', 'LotConfig',
       'LandSlope', 'Neighborhood', 'Condition1', 'Condition2', 'BldgType',
       'HouseStyle', 'OverallQual', 'OverallCond', 'YearBuilt', 'YearRemodAdd',
       'RoofStyle', 'RoofMatl', 'Exterior1st', 'Exterior2nd', 'MasVnrType',
       'MasVnrArea', 'ExterQual', 'ExterCond', 'Foundation', 'BsmtQual',
       'BsmtCond', 'BsmtExposure', 'BsmtFinType1', 'BsmtFinSF1',
       'BsmtFinType2', 'BsmtFinSF2', 'BsmtUnfSF', 'TotalBsmtSF', 'Heating',
       'HeatingQC', 'CentralAir', 'Electrical', '1stFlrSF', '2ndFlrSF',
       'LowQualFinSF', 'GrLivArea', 'BsmtFullBath', 'BsmtHalfBath', 'FullBath',
       'HalfBath', 'BedroomAbvGr', 'KitchenAbvGr', 'KitchenQual',
       'TotRmsAbvGrd', 'Functional', 'Fireplaces', 'FireplaceQu', 'GarageType',
       'GarageYrBlt', 'GarageFinish', 'GarageCars', 'GarageArea', 'GarageQual',
       'GarageCond', 'PavedDrive', 'WoodDeckSF', 'OpenPorchSF',
       'EnclosedPorch', '3SsnPorch', 'ScreenPorch', 'PoolArea', 'PoolQC',
       'Fence', 'MiscFeature', 'MiscVal', 'MoSold', 'YrSold', 'SaleType',
       'SaleCondition', 'SalePrice'],
      dtype='object')

df_train['SalePrice'].describe()

count      1460.000000
mean     180921.195890
std       79442.502883
min       34900.000000
25%      129975.000000
50%      163000.000000
75%      214000.000000
max      755000.000000
Name: SalePrice, dtype: float64

2. 变量分析

import seaborn as sns

# 绘制售价的直方图
sns.distplot(df_train['SalePrice']);

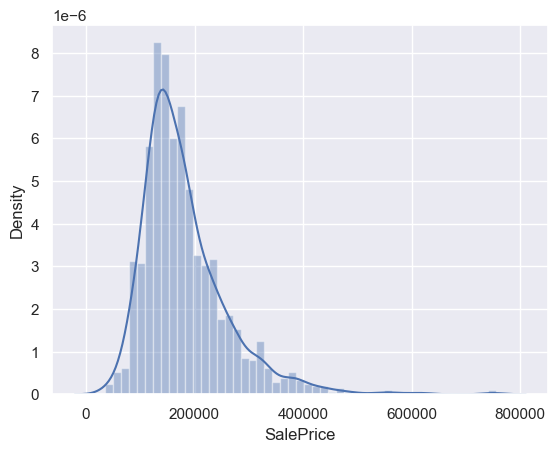
# 输出偏度和峰度
print("Skewness: %f" % df_train['SalePrice'].skew())
print("Kurtosis: %f" % df_train['SalePrice'].kurt())

Skewness: 1.882876
Kurtosis: 6.536282

• 偏度（Skewness）是一种衡量随机变量概率分布的偏斜方向和程度的度量，是统计数据分布非对称程度的数字特征。偏度可以用来反映数据分布相对于对称分布的偏斜程度。偏度的取值范围为 (−∞,+∞)，完全服从正态分布的数据的偏度值为0，偏度值越大，表示数据分布的右侧尾部较长和较厚，称为右偏态或正偏态；偏度值越小，表示数据分布的左侧尾部较长和较厚，称为左偏态或负偏态。
• 峰度（Kurtosis）是一种衡量随机变量概率分布的峰態的指标。峰度高就意味着方差增大是由低频度的大于或小于平均值的极端差值引起的。峰度可以用来度量数据分布的平坦度（flatness），即数据取值分布形态陡缓程度的统计量。

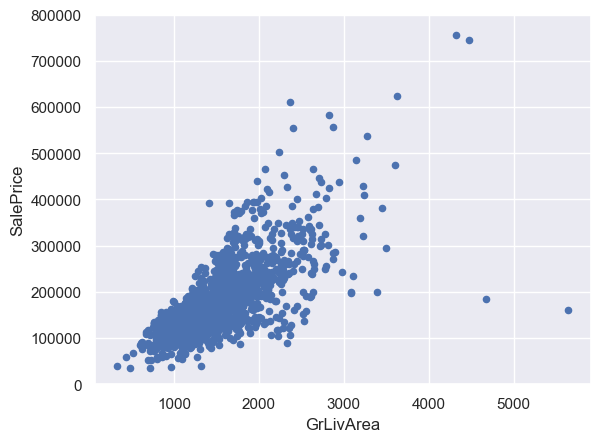
# 绘制GrLivArea（生活面积）的散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));

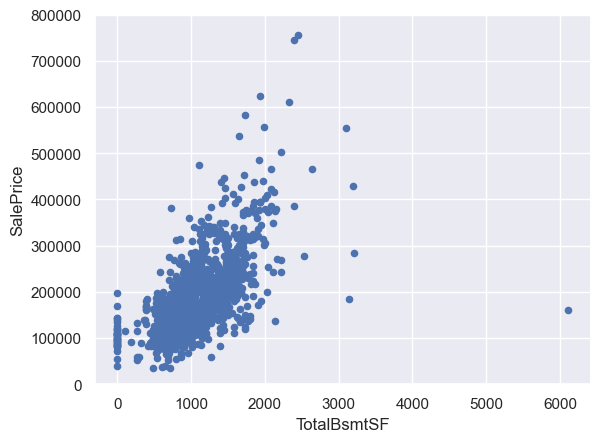
# 绘制TotalBsmtSF（地下室面积）的散点图
var = 'TotalBsmtSF'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));

import matplotlib.pyplot as plt

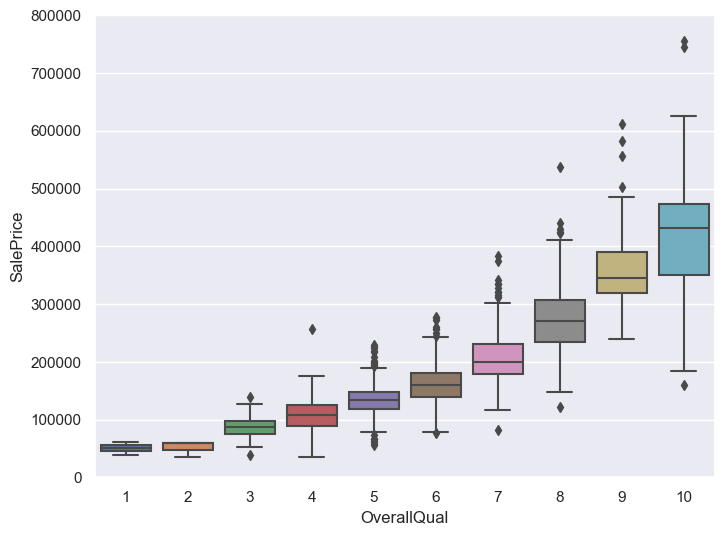
# 绘制OverallQual（房屋整体材料和装修质量）的箱线图
var = 'OverallQual'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(8, 6))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000);

# 绘制YearBuilt（建造年份）的箱线图
var = 'YearBuilt'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
f, ax = plt.subplots(figsize=(16, 8))
fig = sns.boxplot(x=var, y='SalePrice', data=data)
fig.axis(ymin=0, ymax=800000)
plt.xticks(rotation=90);    # 旋转x轴标签90度

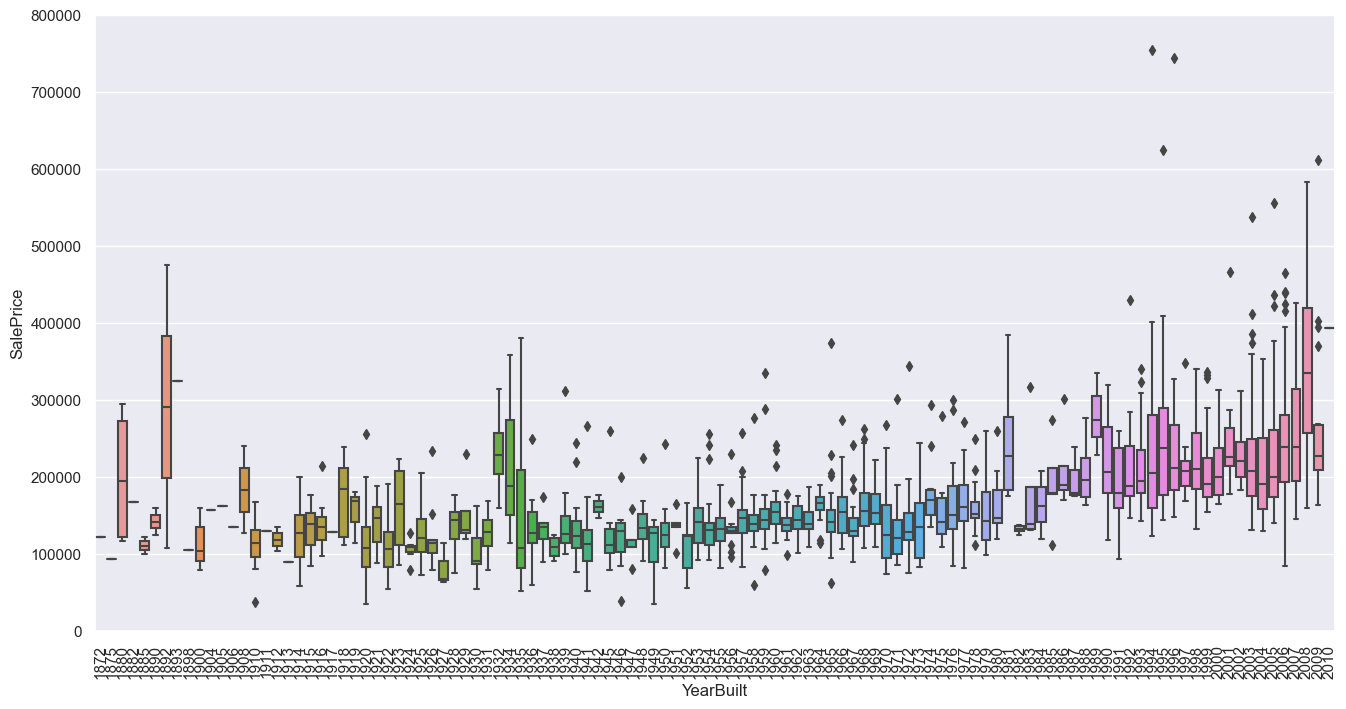
• GrLivArea和TotalBsmtSF与SalePrice呈线性关系。TotalBsmtSF的斜率更大，说明地下室面积对售价的影响更大。
• OverallQual和YearBuilt与SalePrice呈正相关关系。

3. 更进一步的变量分析

第二步只是凭着直觉对数据进行了初步的分析，下面我们将对数据进行更进一步的分析。

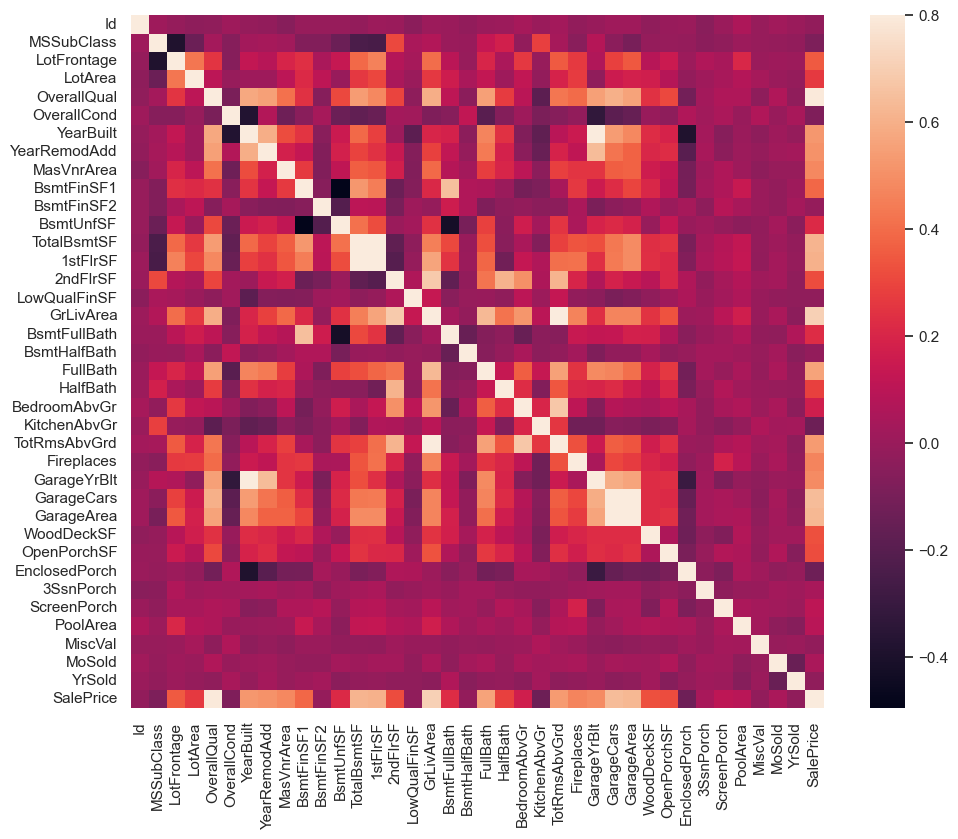
# 绘制变量相关矩阵
corrmat = df_train.corr(numeric_only=True) # 仅对数值型变量进行相关分析
f, ax = plt.subplots(figsize=(12, 9))
sns.heatmap(corrmat, vmax=.8, square=True);

import numpy as np

# SalePrice与其他变量的相关系数
k = 10
cols = corrmat.nlargest(k, 'SalePrice')['SalePrice'].index # 与SalePrice相关系数最大的10个变量的索引
cm = np.corrcoef(df_train[cols].values.T) # 计算相关系数矩阵
sns.set(font_scale=1.25)
hm = sns.heatmap(cm, annot=True, fmt='.2f', annot_kws={'size': 10},
                 yticklabels=cols.values, xticklabels=cols.values)  # 设置annot=True，显示相关系数
plt.show()

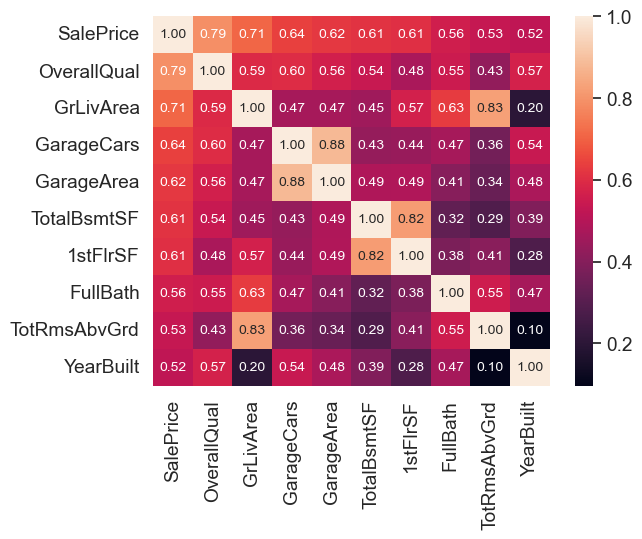
对于GarageCars和GarageArea，两者有很强的关联性，因此选择保留GrageCars，因为它与SalePrice的相关性更高；TotalBsmtSF和1stFloor（First Floor square feet）也有很强的关联性，地下室面积一般情况下不会大于一楼的面积，故选择保留TotalBsmtSF。

因此最终保留了7个与SalePrice关联最大的7个变量，分别是OverallQual、GrLivArea、GarageCars、TotalBsmtSF、FullBath、YearBuilt和YearRemodAdd。

# 绘制变量之间的pairplot散点图
sns.set()
cols = ['SalePrice', 'OverallQual', 'GrLivArea', 'GarageCars', 'TotalBsmtSF',
        'FullBath', 'YearBuilt', 'YearRemodAdd']
sns.pairplot(df_train[cols], size=2.5)
plt.show()

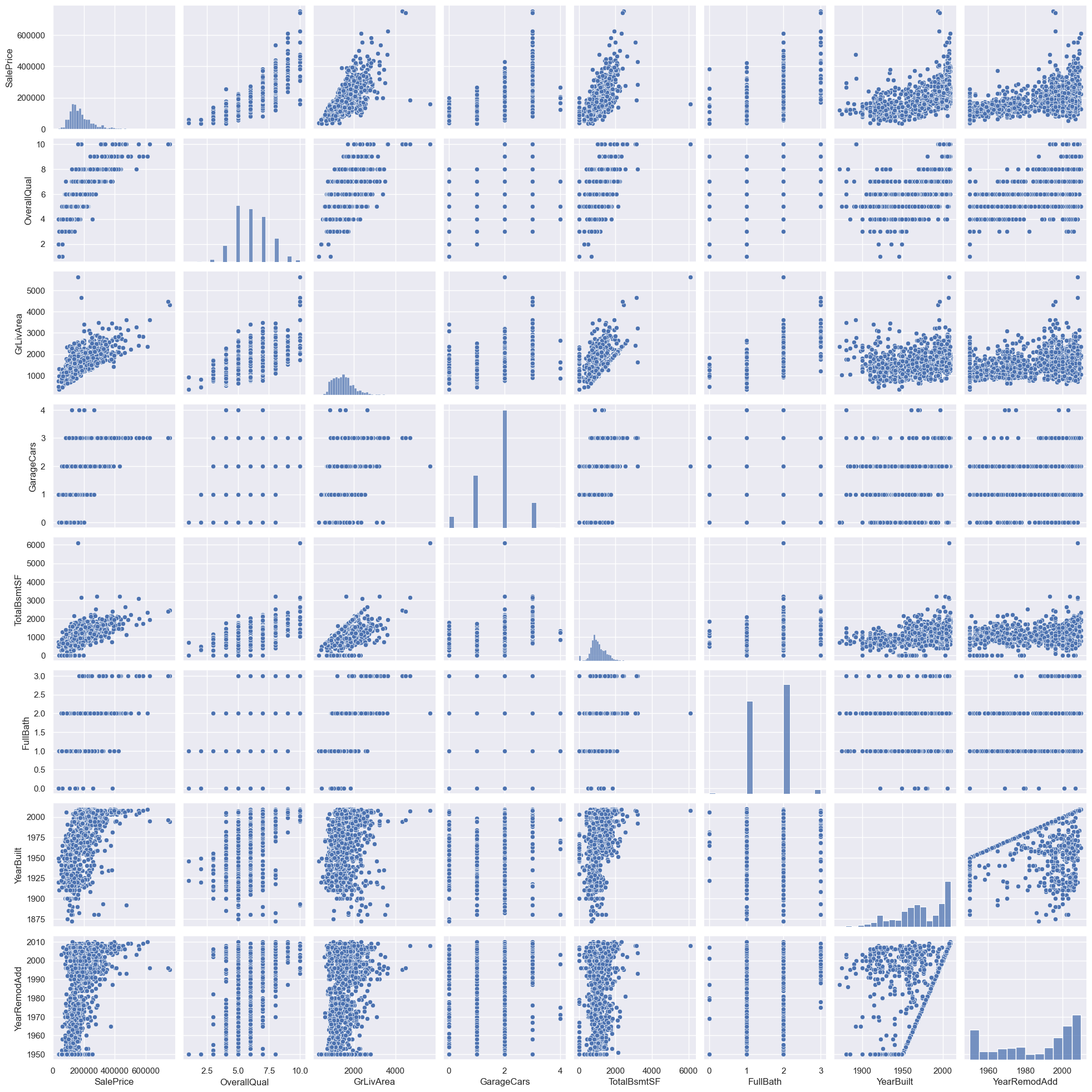
观察成对散点图：

TotalBsmtSF和GrLivArea两者的图像上有一条直线，仿佛边界一般。说明地下室面积和生活面积成正比。就像上面提到的地下室面积和一楼面积的关系一样。

SalePrice和YearBuilt的散点仿佛指数函数一般，说明房价随着建造年份的增加而增加。

4. 缺失值处理

total = df_train.isnull().sum().sort_values(ascending=False) # 统计每个变量的缺失值个数
percent = (df_train.isnull().sum() / len(df_train)).sort_values(ascending=False) # 统计每个变量的缺失值比例
missing_data = pd.concat([total, percent], axis=1, keys=['Total', 'Percent'])
missing_data.head(20)

.dataframe tbody tr th:only-of-type { vertical-align: middle }
\3c pre>\3c code>.dataframe tbody tr th { vertical-align: top }
.dataframe thead th { text-align: right }

	Total	Percent
PoolQC	1453	0.995205
MiscFeature	1406	0.963014
Alley	1369	0.937671
Fence	1179	0.807534
MasVnrType	872	0.597260
FireplaceQu	690	0.472603
LotFrontage	259	0.177397
GarageYrBlt	81	0.055479
GarageCond	81	0.055479
GarageType	81	0.055479
GarageFinish	81	0.055479
GarageQual	81	0.055479
BsmtFinType2	38	0.026027
BsmtExposure	38	0.026027
BsmtQual	37	0.025342
BsmtCond	37	0.025342
BsmtFinType1	37	0.025342
MasVnrArea	8	0.005479
Electrical	1	0.000685
Id	0	0.000000

df_train = df_train.drop((missing_data[missing_data['Total'] > 1]).index, axis=1) # 将缺失数量大于1的列删去
df_train = df_train.drop(df_train.loc[df_train['Electrical'].isnull()].index) # 将Electrical缺失的行删去
df_train.isnull().sum().max() # 检查是否还有缺失值

0

from sklearn.preprocessing import StandardScaler

saleprice_scaled = StandardScaler().fit_transform(df_train['SalePrice'].to_numpy()[:, np.newaxis])

# 输出异常值
low_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][:10]
high_range = saleprice_scaled[saleprice_scaled[:, 0].argsort()][-10:]
print('outer range (low) of the distribution:')
print(low_range)
print('\nouter range (high) of the distribution:')
print(high_range)

outer range (low) of the distribution:
[[-1.83820775]
 [-1.83303414]
 [-1.80044422]
 [-1.78282123]
 [-1.77400974]
 [-1.62295562]
 [-1.6166617 ]
 [-1.58519209]
 [-1.58519209]
 [-1.57269236]]

outer range (high) of the distribution:
[[3.82758058]
 [4.0395221 ]
 [4.49473628]
 [4.70872962]
 [4.728631  ]
 [5.06034585]
 [5.42191907]
 [5.58987866]
 [7.10041987]
 [7.22629831]]

# 重新绘制GrLivArea和SalePrice的散点图
var = 'GrLivArea'
data = pd.concat([df_train['SalePrice'], df_train[var]], axis=1)
data.plot.scatter(x=var, y='SalePrice', ylim=(0, 800000));

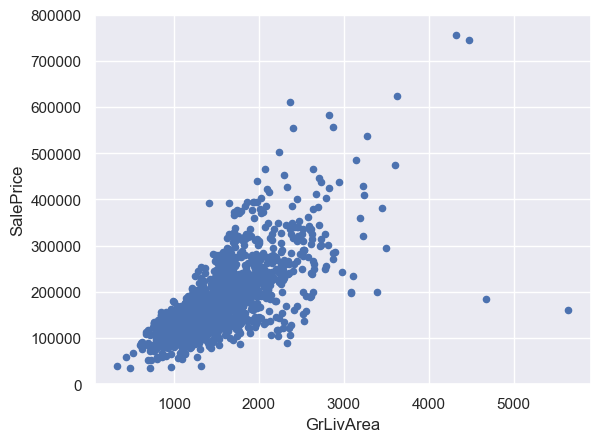
上图中右下角的两个点是异常值，因为它们的GrLivArea很大，但是售价很低。因此将它们删除。

lines = df_train.sort_values(by='GrLivArea', ascending=False)[:2]
df_train = df_train.drop(lines.index)

5. 测试数据

对于结果的计算分析，需要建立在一定的数据假设上。通常，需要考虑这四种情况：

• 正态性（Normality）：许多的统计方法测试都是基于数据是正态分布的情况，因此，如果数据服从正态分布能避免很多问题。
• 同方差性（Homoscedasticity）：同方差性是指因变量的方差在自变量的每个水平上都相等。同方差性是许多统计检验的一个前提条件，如果数据不符合同方差性，可能会导致结果不准确。
• 线性性（Linearity）：线性模型的一个前提条件是自变量和因变量之间的关系是线性的，如果不是线性的，可能需要对数据进行转换。
• 不存在相关错误（Absence of correlated errors）：相关错误是指数据中的一个观测值的误差与另一个观测值的误差相关。例如，如果两个观测值的误差都是正的，那么它们之间就存在正相关错误。相关错误可能会导致结果不准确。

from scipy.stats import norm
from scipy import stats

# 绘制直方图与正态概率图
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

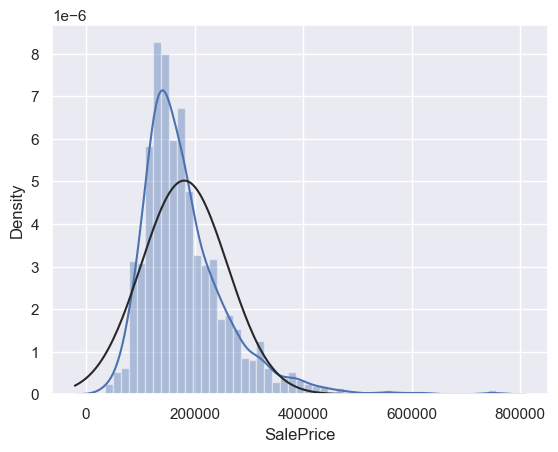
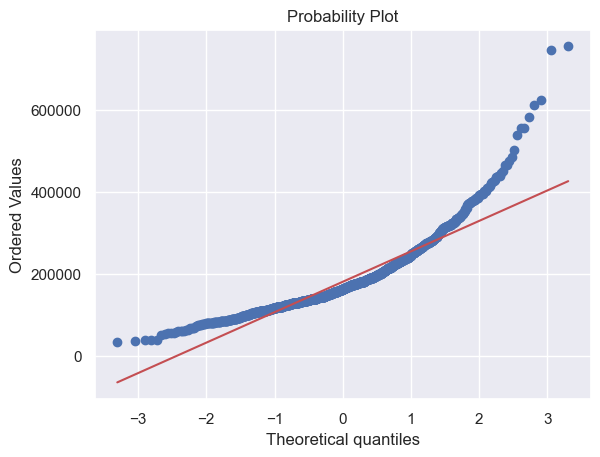
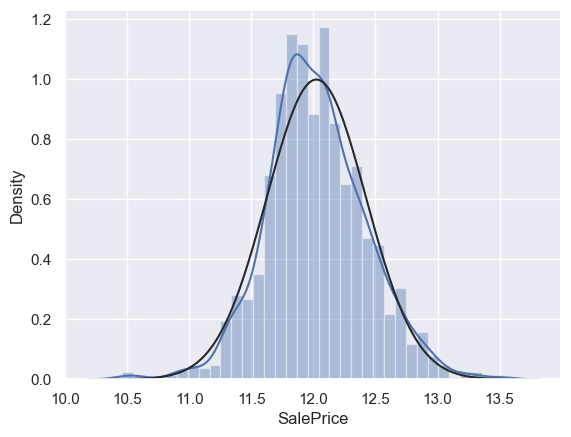
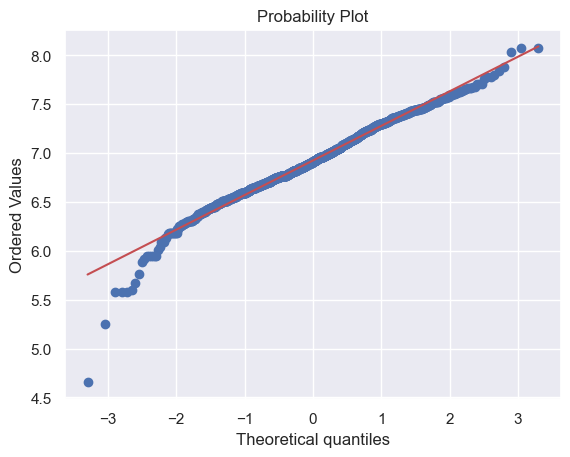
# 对SalePrice进行log转换使其更接近正态分布，并重新绘制直方图与正态概率图
df_train['SalePrice'] = np.log(df_train['SalePrice'])
sns.distplot(df_train['SalePrice'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['SalePrice'], plot=plt)

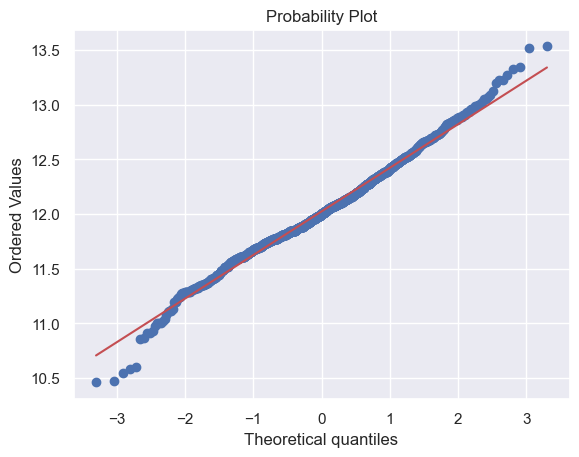
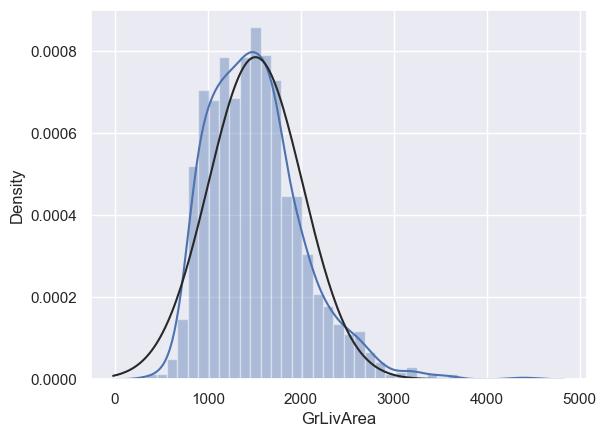
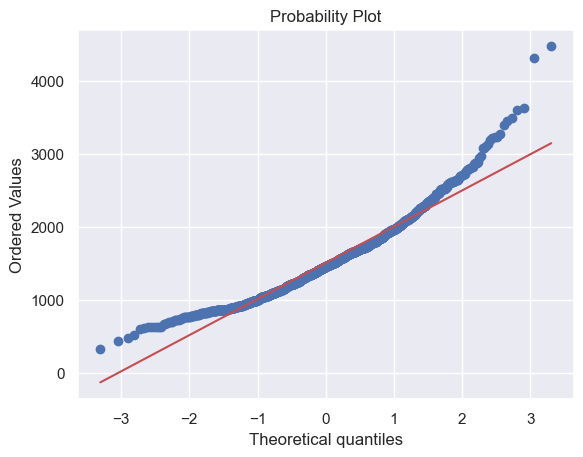
# 同理，对GrLivArea绘制直方图与正态概率图
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['GrLivArea'], plot=plt)

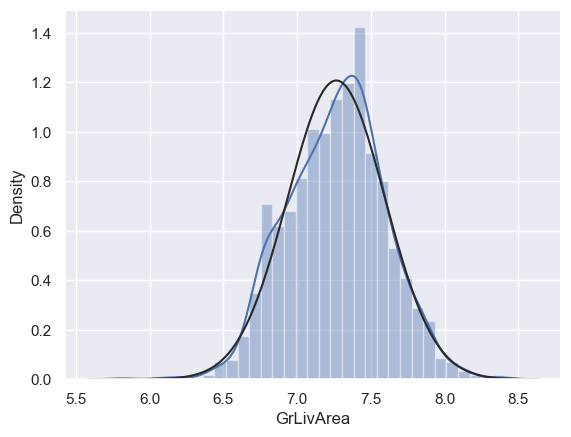
# 对GrLivArea进行log转换使其更接近正态分布，并重新绘制直方图与正态概率图
df_train['GrLivArea'] = np.log(df_train['GrLivArea'])
sns.distplot(df_train['GrLivArea'], fit=norm)
fig = plt.figure()
res= stats.probplot(df_train['GrLivArea'], plot=plt)

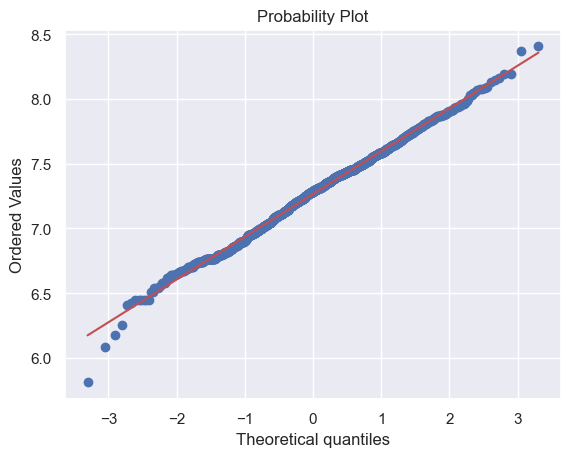
# 还有TotalBsmtSF
sns.distplot(df_train['TotalBsmtSF'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train['TotalBsmtSF'], plot=plt)

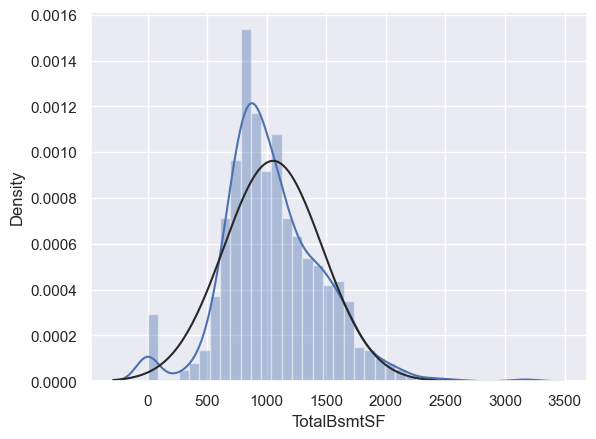
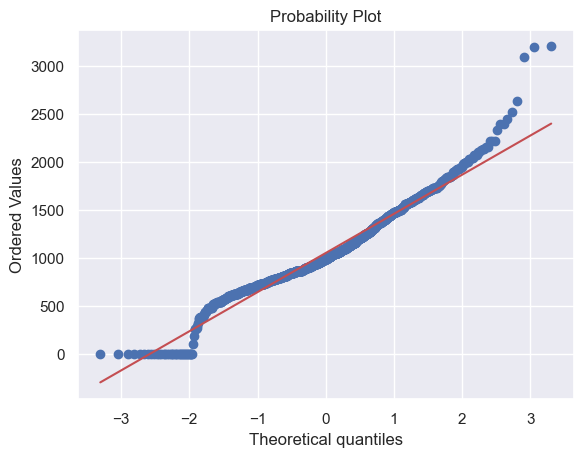
由于一些房子没有地下室，导致有很多0值，因此不能对TotalBsmtSF进行log转换。

这里创建一个新的变量，如果TotalBsmtSF>0，则为1，否则为0。

df_train['HasBsmt'] = pd.Series(len(df_train['TotalBsmtSF']), index=df_train.index)
df_train['HasBsmt'] = 0
df_train.loc[df_train['TotalBsmtSF'] > 0, 'HasBsmt'] = 1

# 对HasBsmt为1的数据进行log转换
df_train.loc[df_train['HasBsmt'] == 1, 'TotalBsmtSF'] = np.log(df_train['TotalBsmtSF'])
sns.distplot(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], fit=norm)
fig = plt.figure()
res = stats.probplot(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], plot=plt)

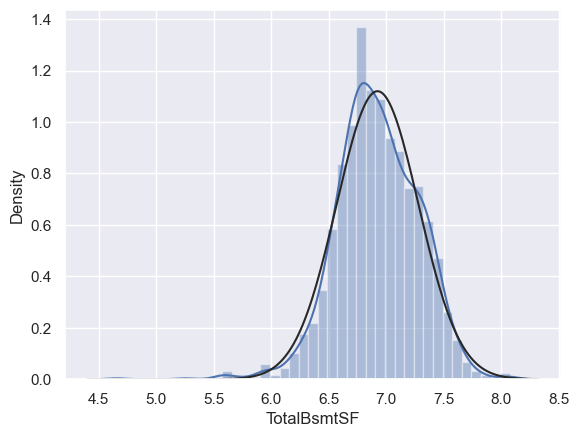
对于同方差的检验，可以绘制散点图。如果散点呈现锥形（就像之前画的），这意味着数据的方差随着自变量的增加而增加，通常被称为异方差；变量是同方差，散点的数据应该分布在一条直线附近。

现在我们来看一下经过log运算后的SalePrice和GrLivArea还有TotalBsmtSF的散点图。

plt.scatter(df_train['GrLivArea'], df_train['SalePrice']);

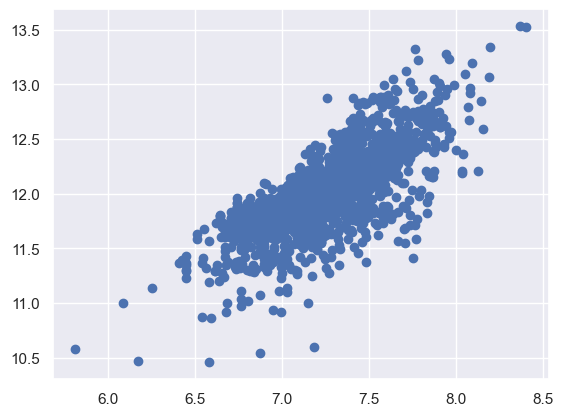
plt.scatter(df_train[df_train['TotalBsmtSF'] > 0]['TotalBsmtSF'], df_train[df_train['TotalBsmtSF'] > 0]['SalePrice']);

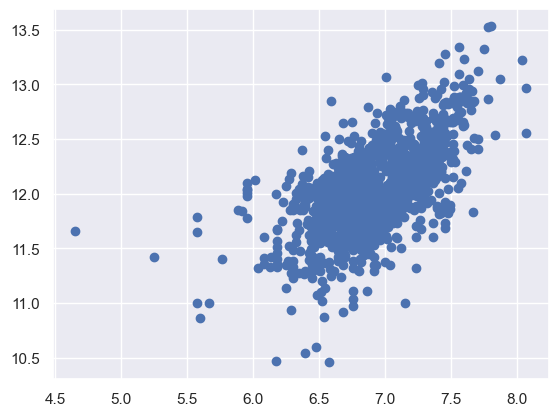
6. 哑变量

# 将类别变量转换为哑变量
df_train = pd.get_dummies(df_train)

总结

本次使用了pandas库和seaborn库对数据进行了初步的分析，对数据的缺失值进行了处理，对数据进行了转换，最后将类别变量转换为哑变量。