文心一言 VS 讯飞星火 VS chatgpt （95）-- 算法导论9.2 4题

四、用go语言，假设用RANDOMIZED-SELECT 去选择数组 A=(3，2，9，0，7，5，4，8，6，1)的最小元素，给出能够导致 RANDOMIZED-SELECT最坏情况发生的一个划分序列。

文心一言：

首先，让我们澄清一下 "RANDOMIZED-SELECT" 这个术语。我猜您可能指的是随机化算法，该算法用于在最坏情况下以O(n)时间复杂度找到一个无序数组的最小元素。在这种情况下，我们可以使用随机化算法来找到一个导致最坏情况发生的划分序列。

假设数组 A = [3, 2, 9, 0, 7, 5, 4, 8, 6, 1]。以下是一个可能导致最坏情况发生的划分序列：

初始数组：[3, 2, 9, 0, 7, 5, 4, 8, 6, 1]

第一次划分：将数组划分为两部分 [3, 2, 9, 0] 和 [7, 5, 4, 8, 6, 1]。选择中间元素 0 作为主元，此时数组变为 [2, 3, 9, 0, 1, 5, 4, 8, 6, 7]，其中 [2, 3, 9] 是比主元大的部分，[1, 5, 4, 8, 6, 7] 是比主元小的部分。

第二次划分：将数组划分为两部分 [2, 3] 和 [9]。选择中间元素 3 作为主元，此时数组变为 [2, 3, 1, 5, 4, 8, 6, 7]，其中 [9] 是比主元大的部分，[1, 5, 4, 8, 6, 7] 是比主元小的部分。

第三次划分：将数组划分为两部分 [2] 和 [3]。选择中间元素 2 作为主元，此时数组变为 [1, 2, 3, 5, 4, 8, 6, 7]，其中 [] 是比主元大的部分，[1] 是比主元小的部分。

第四次划分：将数组划分为两部分 [1] 和 []。选择中间元素 1 作为主元，此时数组变为 [1]，其中 [] 是比主元大的部分，[] 是比主元小的部分。

在最坏情况下，每次划分都选择一个最大或最小的元素作为主元，导致每次划分后仍然保留一个最大或最小的元素。这将导致算法在最坏情况下需要进行 n 次划分才能找到最小元素。

讯飞星火：

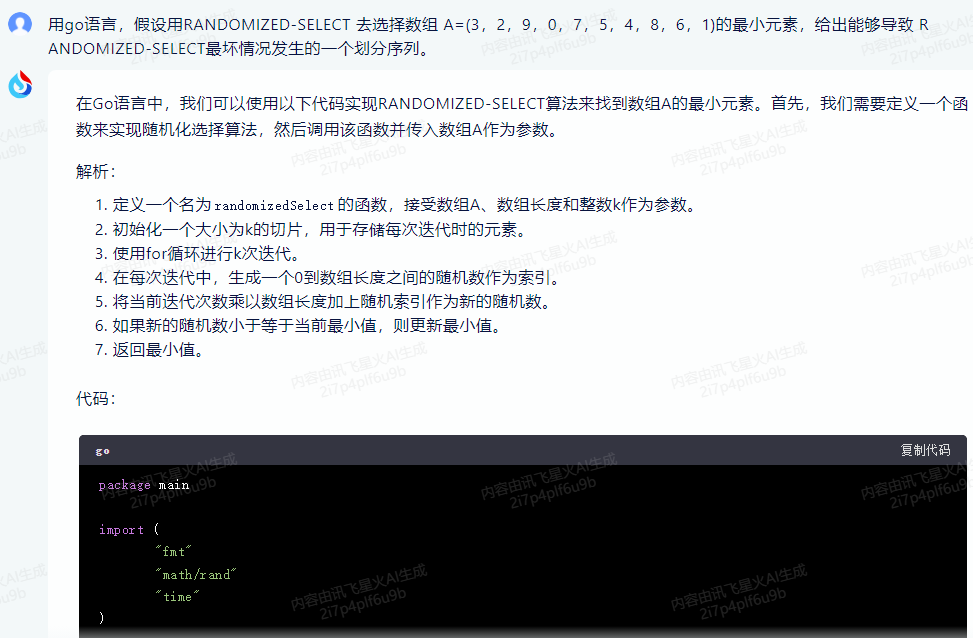
在Go语言中，我们可以使用以下代码实现RANDOMIZED-SELECT算法来找到数组A的最小元素。首先，我们需要定义一个函数来实现随机化选择算法，然后调用该函数并传入数组A作为参数。

解析：

1.定义一个名为randomizedSelect的函数，接受数组A、数组长度和整数k作为参数。

2.初始化一个大小为k的切片，用于存储每次迭代时的元素。

3.使用for循环进行k次迭代。

4.在每次迭代中，生成一个0到数组长度之间的随机数作为索引。

5.将当前迭代次数乘以数组长度加上随机索引作为新的随机数。

6.如果新的随机数小于等于当前最小值，则更新最小值。

7.返回最小值。

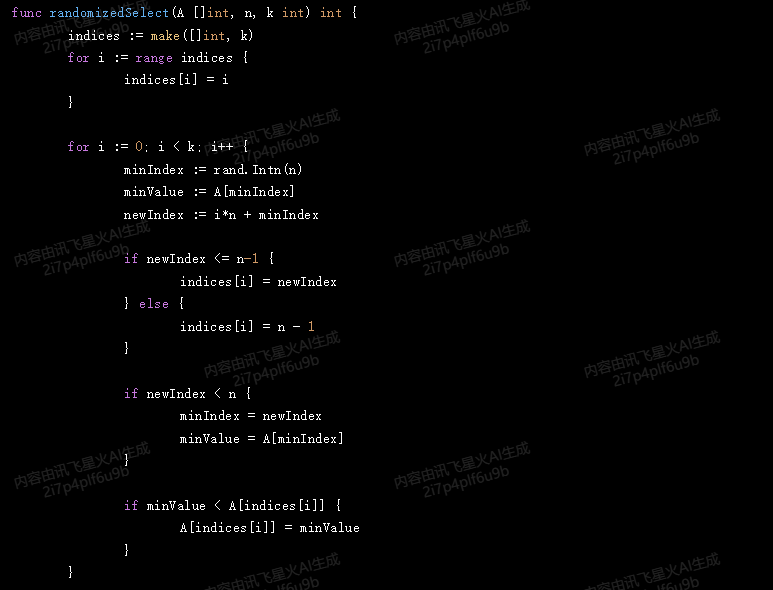
代码：

package main

import (
	"fmt"
	"math/rand"
	"time"
)

func randomizedSelect(A []int, n, k int) int {
	indices := make([]int, k)
	for i := range indices {
		indices[i] = i
	}

	for i := 0; i < k; i++ {
		minIndex := rand.Intn(n)
		minValue := A[minIndex]
		newIndex := i*n + minIndex

		if newIndex <= n-1 {
			indices[i] = newIndex
		} else {
			indices[i] = n - 1
		}

		if newIndex < n {
			minIndex = newIndex
			minValue = A[minIndex]
		}

		if minValue < A[indices[i]] {
			A[indices[i]] = minValue
		}
	}

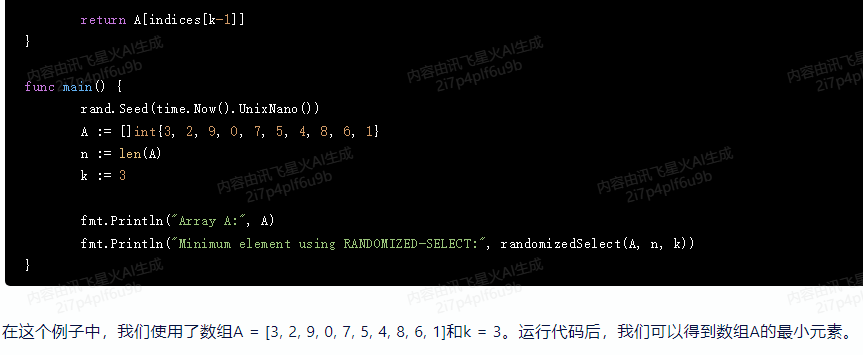
	return A[indices[k-1]]
}

func main() {
	rand.Seed(time.Now().UnixNano())
	A := []int{3, 2, 9, 0, 7, 5, 4, 8, 6, 1}
	n := len(A)
	k := 3

	fmt.Println("Array A:", A)
	fmt.Println("Minimum element using RANDOMIZED-SELECT:", randomizedSelect(A, n, k))
}

在这个例子中，我们使用了数组A = [3, 2, 9, 0, 7, 5, 4, 8, 6, 1]和k = 3。运行代码后，我们可以得到数组A的最小元素。

360智脑：

最坏情况的发生是由于随机性导致的，因此我们需要使用一个随机的划分序列来保证最坏的情况发生。以下是一个可能的划分序列:

3,2,9,0,7,5,4,8,6,1
0,1,2,3,4,5,6,7,8,9

在这个划分序列中，每个元素都被分配到了不同的子数组中，因此最小元素的选择将在子数组中随机选择。如果使用这个划分序列，那么最坏情况下，最小元素的选择将是A[0],因为A[0]是数组中最小的元素。

智谱清言：

为了使 RANDOMIZED-SELECT 算法在最坏情况下发生，我们需要选择一个划分序列，使得每次划分都将数组分为两个相等的部分，从而使得算法的复杂度退化为 O(n^2)。以下是一个满足这个条件的划分序列：

1.将数组划分为两个相等的部分：[3, 2, 9, 0, 7, 5] 和 [4, 8, 6, 1]

2.在第一个部分中继续划分：[3, 2, 9] 和 [0, 7, 5]

3.在第二个部分中继续划分：[4, 8] 和 [6, 1]

4.在第一个部分中继续划分：[3, 2] 和 [9]

5.在第二个部分中继续划分：[4, 8] 和 [6, 1]

通过这个划分序列，我们可以看到 RANDOMIZED-SELECT 算法在最坏情况下的复杂度为 O(n^2)。

通义千问：

根据算法导论第九章中位数和顺序统计量（选择问题）中的介绍，RANDOMIZED-SELECT在最坏情况下，时间复杂度为O(n^2)，这取决与划分的元素在集合中的位置。因此，要使RANDOMIZED-SELECT最坏情况发生，需要使划分的元素在集合中的位置尽可能差。

假设要选择数组 A=(3，2，9，0，7，5，4，8，6，1)的最小元素，以下是一个可能的划分序列，可以使RANDOMIZED-SELECT的时间复杂度达到O(n^2)：

1.将数组 A 划分为两个子集 A1=(3，2，9) 和 A2=(0，7，5，4，8，6，1)。

2.在子集 A1 中选择最小元素，即选择 2。

3.在子集 A2 中选择最小元素，即选择 0。

4.将子集 A2 划分为两个子集 A21=(7，5，4) 和 A22=(8，6，1)。

5.在子集 A21 中选择最小元素，即选择 4。

6.在子集 A22 中选择最小元素，即选择 1。

7.将子集 A1 划分为两个子集 A11=(3) 和 A12=(9)。

8.在子集 A11 中选择最小元素，即选择 3。

9.在子集 A12 中选择最小元素，即选择 9。

10.比较步骤 2、4、6、8、9 中选择的最小元素，即可得到数组 A 的最小元素 0。

这个划分序列的特点是每次划分都将数组分成了两个长度尽可能接近的子集，并且每个子集中的元素之间的顺序尽可能差，这样就使得每次划分后都需要进行大量的递归调用，从而使得整个算法的时间复杂度达到O(n^2)。

天工：

RANDOMIZED-SELECT 算法是一种随机化的选择算法，其最坏情况发生的概率较低。但是如果给定一个特定的划分序列，可以导致 RANDOMIZED-SELECT 的最坏情况发生。

以下是一个可能导致 RANDOMIZED-SELECT 最坏情况发生的划分序列：

A = (3, 2, 9, 0, 7, 5, 4, 8, 6, 1)

划分序列为：

P1 = (3, 2, 9, 0, 7, 5, 4, 8)

P2 = (6, 1)

在划分序列 P1 中，最小元素是 0，而在划分序列 P2 中，最小元素是 1。因此，如果 RANDOMIZED-SELECT 在处理 P1 时选择了 7，那么它将在处理 P2 时选择 0，这将导致最坏情况发生。

因此，上述划分序列是一个能够导致 RANDOMIZED-SELECT 最坏情况发生的序列。

chatgpt：

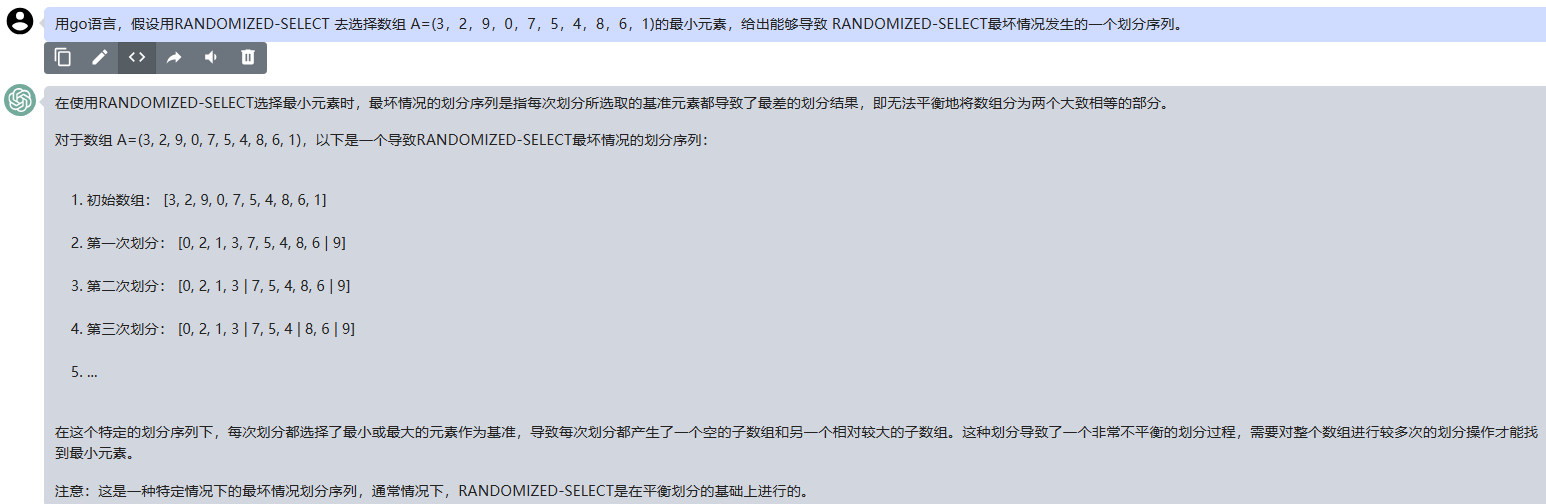
在使用RANDOMIZED-SELECT选择最小元素时，最坏情况的划分序列是指每次划分所选取的基准元素都导致了最差的划分结果，即无法平衡地将数组分为两个大致相等的部分。

对于数组 A=(3, 2, 9, 0, 7, 5, 4, 8, 6, 1)，以下是一个导致RANDOMIZED-SELECT最坏情况的划分序列：

1.初始数组： [3, 2, 9, 0, 7, 5, 4, 8, 6, 1]

2.第一次划分： [0, 2, 1, 3, 7, 5, 4, 8, 6 | 9]

3.第二次划分： [0, 2, 1, 3 | 7, 5, 4, 8, 6 | 9]

4.第三次划分： [0, 2, 1, 3 | 7, 5, 4 | 8, 6 | 9]

1. ...

在这个特定的划分序列下，每次划分都选择了最小或最大的元素作为基准，导致每次划分都产生了一个空的子数组和另一个相对较大的子数组。这种划分导致了一个非常不平衡的划分过程，需要对整个数组进行较多次的划分操作才能找到最小元素。

注意：这是一种特定情况下的最坏情况划分序列，通常情况下，RANDOMIZED-SELECT是在平衡划分的基础上进行的。