leetcode:354 俄罗斯套娃信封问题(LIS)

解题思路：

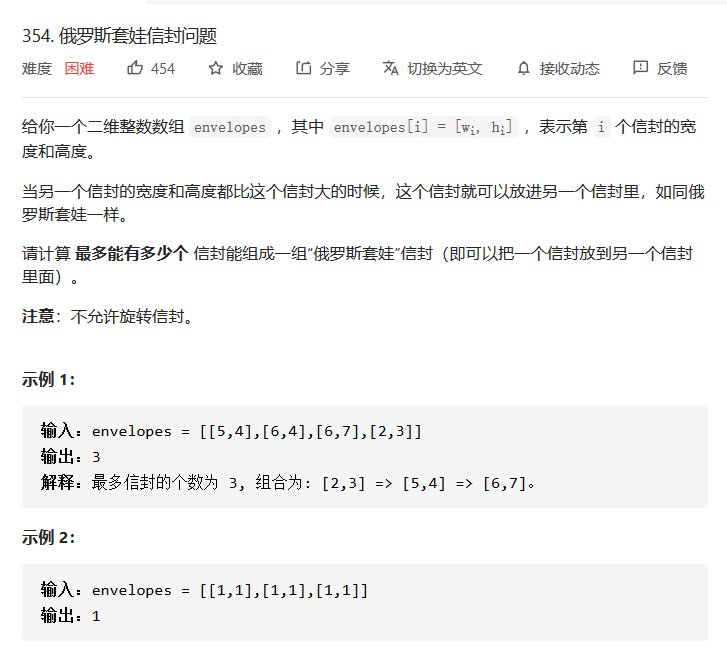
根据题意，不难发现组合的元素，他们的长宽都是单调递增的，因此可以转化为最长上升子序列问题。

首先按照长度从小到大对信封进行排序，长度相同，按照宽度从大到小进行排序。因为当长度相同，因为可能会把相同长的信封当做长度不同的信封给装起来了，如果宽度从大到小排序，就不会出现覆盖长度相同的情况。

然后就是正常LIS方法，在coding的过程中，为了防止出现序列长度和信封长度相同的情况下出现保留了宽度较长的信封而没有保存宽度较短的信封，用了list存储结尾值，后来发现是没有必要的操作，因为不可能出现这种情况。。。

def maxEnvelopes(envelopes):
    # dp[i]表示以第i个元素结尾的最长子序列长度
    dp= [0]*len(envelopes)+[0]
    # mx[j]表示长度为j的序列结尾值是多少,考虑到在信封的长度有可能重复,因此用list存储
    mx =[[0]] + [[100000] for i in range(len(envelopes))]
    # 按照长从小到大排，长度相同按照宽从大到小排
    a = sorted(envelopes,key = lambda x:(x[0],-x[1])) #
    length = len(a)
    a = [[0, 0]] + a +[[0,0]]
    #填充下标0，使元素从1开始算
    for i in range(1,length+1):
        #如果当前信封的长和上一个不同，说明已经处理完重复的信封了，后面的信封长度都比之前的长
        #因此，根据最优解的依赖关系，我们仅需保留mx[j]中结尾值最小的元素
        if a[i][0]!=a[i-1][0]:
            xx = mx.index([100000]) #优化查询，降低时间复杂度，使得整体复杂度由N*N降低到N*logN
            for j in range(xx,-1,-1):
                mini = min(mx[j])
                mx[j] = [mini]
        xx = mx.index([100000]) #优化查询，降低时间复杂度，使得整体复杂度由N*N降低到N*logN
        for j in range(xx,-1,-1):
            flag =False
            for k in mx[j]:
                if a[i][1] > k: #只需要比mx[j]中某一个值大就可以构造成长度为j+1的子序列
                    dp[i] = j+1
                    mx[dp[i]].append(a[i][1])
                    flag = True
                    break
            if flag:
                break
    #print(mx)
    return max(dp)

 1 简化版
 2 class Solution(object):
 3     def maxEnvelopes(self,envelopes):
 4        # dp[i]表示以第i个元素结尾的最长子序列长度
 5         dp= [0]*len(envelopes)+[0]
 6         # mx[j]表示长度为j的序列结尾值是多少,考虑到在信封的长度有可能重复,因此用list存储
 7         mx =[0] + [100000 for i in range(len(envelopes))]
 8         # 按照长从小到大排，长度相同按照宽从大到小排
 9         a = sorted(envelopes,key = lambda x:(x[0],-x[1])) #
10         length = len(a)
11         a = [[0, 0]] + a +[[0,0]]
12         #填充下标0，使元素从1开始算
13         for i in range(1,length+1):
14             xx = mx.index(100000) #优化查询，降低时间复杂度，使得整体复杂度由N*N降低到N*logN
15             for j in range(xx,-1,-1):
16                 if a[i][1] > mx[j]:
17                     dp[i] = j+1
18                     mx[dp[i]]= min(mx[dp[i]],a[i][1])
19                     break
20         #print(mx)
21         return max(dp)