bzoj3716/4251 [PA2014]Muzeum

传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=3716

http://www.lydsy.com/JudgeOnline/problem.php?id=4251

【题解】

非常妙的网络流转化

首先可以把警卫和宝藏看成最大权闭合子图，用最小割的那种建模方法，即一开始加进来所有宝藏的价值

然后S连宝藏，警卫连T，有覆盖关系的连inf

那么就是一个最小割，复杂度是$O(maxflow(n+m, nm)$，显然承受不了。

由于最小割和最大流等价，所以转化最大流考虑。

问题变为

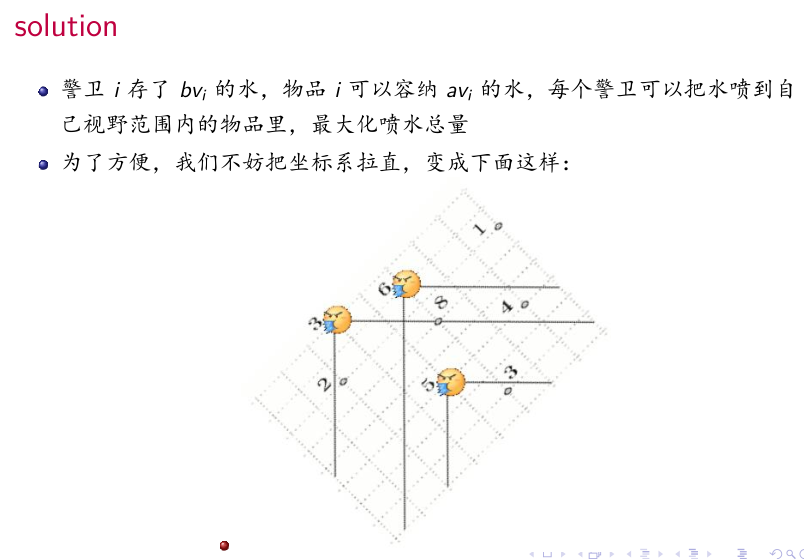
那么按x从大到小排序，每次2种操作：加入一个物品；有一个警卫可以喷水给所有y小于它物品。

显然按照y从大到小喷最优，因为小的限制条件小。

用个set维护即可，注意set的时候lower_bound只能s.lower_bound(...)，不能lower_bound(s.begin(), s.end(), ..)！！！

# include <set>
# include <stdio.h>
# include <string.h>
# include <iostream>
# include <algorithm>
// # include <bits/stdc++.h>

using namespace std;

typedef long long ll;
typedef long double ld;
typedef unsigned long long ull;
const int N = 2e5 + ;
const int mod = 1e9+;
const ll inf = 5e18;

inline int getint() {
    int x = , f = ; char ch = getchar();
    while(!isdigit(ch)) {
        if(ch == '-') f = ;
        ch = getchar();
    }
    while(isdigit(ch)) {
        x = (x<<) + (x<<) + ch - '';
        ch = getchar();
    }
    return f ? x : -x;
}

int n, m, W, H;
struct pa {
    ll x, y; int v;
    pa () {}
    pa (ll x, ll y, int v) : x(x), y(y), v(v) {}
    inline friend bool operator < (pa a, pa b) {
        return a.y < b.y || (a.y == b.y && a.x < b.x);
    }
}a[N], b[N];

struct option {
    ll x, y; int v, op;
    option() {}
    option(int op, ll x, ll y, int v) : op(op), x(x), y(y), v(v) {}
    inline friend bool operator < (option a, option b) {
        return a.x < b.x || (a.x == b.x && a.op > b.op);
    }
}p[N + N]; 

set<pa> s;
set<pa>::iterator it;

int main() {
    ll ans = ;
    cin >> n >> m >> W >> H;
    for (int i=; i<=n; ++i) {
        a[i].x = 1ll * H * getint(), a[i].y = 1ll * W * getint(), a[i].v = getint();
        p[i] = option(, a[i].x - a[i].y, a[i].x + a[i].y, a[i].v); ans += a[i].v;
    }
    for (int i=; i<=m; ++i) {
        b[i].x = 1ll * H * getint(), b[i].y = 1ll * W * getint(), b[i].v = getint();
        p[n + i] = option(, b[i].x - b[i].y, b[i].x + b[i].y, b[i].v);
    }

    // maxflow
    int pn = n + m;
    sort(p+, p+pn+); s.clear(); 

    for (int i=pn; i; --i) {
        if(p[i].op == ) s.insert(pa(p[i].x, p[i].y, p[i].v));
        else {
            int cv = p[i].v;
            pa r = pa(inf, p[i].y, cv), t;
            while(cv && s.size()) {
                it = s.upper_bound(r);
                if(it == s.begin()) break;
                --it; t = *it; s.erase(it);
                int tmp = min(t.v, cv);
                cv -= tmp, t.v -= tmp; ans -= tmp;
                if(t.v > ) s.insert(t);
            }
        }
    }

    cout << ans;

    return ;
}