学习笔记 - Ford-Fulkerson & EK

Ford-Fulkerson & EK - 学习笔记

之前网络流什么的快忘完了

老师讲课的时候一脸懵逼……开始系统复习，从最大流开始

标签：网络流-最大流

---

『预备』

首先复习了网络流的概念——

网络流是一个有向图，每一条边有一个流量限制（也可以叫做边权），图上有且仅有两个特殊点：源点-入度为0、汇点-出度为0。除此之外的所有点都有出度和入度。

网络流类似于“水流”，源点就相当于“无穷的水源”，从源点出发向其相邻边“流水”，边上“水”的流量不能超过其流量限制（容量限制），且对于每个点（除源点、汇点），流入该点的“水量”等于该点流出的“水量”（流守恒性）。

其次网络流具有斜对称性，即对于一条边，若它的流量为f，则它的反向边流量为 -f。

（下面简写源点为Begin，汇点为End，网络的边集为 E、点集为 V）

用式子的方法总结一下网络流所具有的性质：

定义\(f(u,v)\)表示u到v的边的流量，\(c(u,v)\)表示u到v的边的流量限制（容量）；只对相邻的 u,v 有此定义。

\[\begin{cases}
f(u,v)<c(u,v)\\
f(u,v)=-f(v,u)\\
\sum_v f(u,v)=\sum_w f(w,u)
\end{cases}
\]

定义网络流的 流f 为：\(f=\sum_v f(Begin,v)=\sum_w f(w,End)\)

定义u到v的边的残留容量r(u,v)为：\(r(u,v)=c(u,v)-f(u,v)\)

最大流即流网络中的最大流值。

EK算法是对Ford-Fulkerson方法的实现。

---

『Ford-Fulkerson方法』

「残留网络&增广路」

如果 \(r(u,v)>0\)，则边 (u,v) 在残留网络中。

增广路是残留网络中从 Begin 到 End 的一条路径 P，\(\delta(P)=\min\{r(u,v)\},(u,v)\in P\) 表示增广路P的残留容量。

「方法」

Ford-Fulkerson方法的主要思想是先构造残余， DFS 找到一条增广路，然后找到增广路上的流量 \(\delta\)，将增广路上的每一条边的流量限制都减去 \(\delta\)、每一条边都反向边都流量限制都加上 \(\delta\) 。

为什么要把反向边的流量限制加上 \(\delta\) 呢？我们来看一个简单的例子：



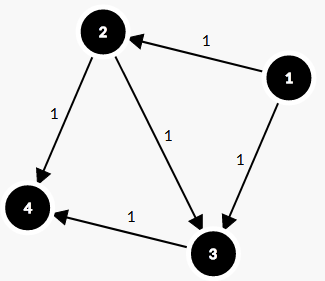
如果我们一开始选择流“1-2-3-4”，那么我们得到流的大小为1，但是显然我们可以选择流“1-2-4 , 1-3-4”，流的大小为2。

如果先流“1-2-3-4”，那么我们就相当于确定了边 (2,3) 必须流，但是这是不一定的。我们给它的反向边 (3,2) 加上 \(\delta\)（最初所有边的反向边的流量限制都为0），那么下一次我们流过它的反向边 (3,2) 时，就相当于“撤销”了流过 (2,3)。然后两次的流量之和就是最大流。

为什么这样是正确的？

让我们手推一下这张图的最大流过程：先找到了“1-2-3-4”，然后 (1,2)(2,3)(3,4) 的流量限制减去10，(2,1)(3,2)(4,3) 加上10；再流过 “1-3-2-4”。就相当于把原来“1-2-3-4”的(2,3)断开，接上(2,4)形成“1-2-4”；而断开过后的“2-3-4”中，流过反向边(3,2)使得(2,3)的流被撤销，再接上(1,3)就形成“1-3-4”。

---

『EK算法』

一种比较基础的对Ford-Fulkerson方法的实现，基于BFS。

首先定义一些数组，方便后面阐述：

(1) vis[u] 表示点 u 在该次BFS中是否被访问过

(2) flw[u] 表示该次BFS中从源点开始流到点 u 的流最大的值（也就是源点BFS到u的路径上的边的最小的流量限制）

(3) preedg[u] 表示该次BFS中是从哪一条边流到u的

「BFS部分」

从源点开始，BFS遍历整个流网络，要求经过的有向边的流量限制严格大于0，并且不重复经过同一个点。当遍历到汇点时，返回当前流值。

假设现在要从u流到v，先要保证 vis[v] == 0 并且 (u,v) 的流量限制大于0。然后标记 vis[v] ，再记录 preedg[v] 为当前边的编号；flw[v] 的计算类似于 dp，因为流值最大不超过 (u,v) 的限制，那么递推式也非常显然 \(flw[v]=\min\{flw[u],c(u,v)\}\)。

如果v就是汇点，则返回 flw[v]，否则将v压入队列。

如果最后无法到达汇点，则返回0，表示无增广路。

「EK算法主部分」

先BFS判断当前是否有增广路，如果有，则BFS返回值则为增广路的流量 \(\delta\)，则从v沿着增广路倒过来回到源点，并将增广路上的边的流量限制减去 \(\delta\)，增广路上的边的反向边的流量限制加上 \(\delta\) 。直到没有增广路（BFS返回值为0），退出循环。

其实就是把 Ford-Fulkerson 方法模拟了一遍。

因此EK算法的时间复杂度并不理想，但毕竟它是（似乎是）最大流算法中最为稳定的算法，有其存在的价值。

「模板代码」

以〔洛谷 P2740〕为原题的代码~

/*Lucky_Glass*/
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
const int N=200;
struct FLOWGRAPH{
    struct NODE{
        int to,nxt,lim,rev;
        NODE(){}
        NODE(int _to,int _nxt,int _lim,int _rev):
            to(_to),nxt(_nxt),lim(_lim),rev(_rev){}
    }nod[N*2+7];
    int cnt,adj[N+7];
    void Rebuild(){
        memset(adj,-1,sizeof adj);
        cnt=0;
    }
    void AddEdge(int u,int v,int lim){
        int A=++cnt,B=++cnt;
        nod[A]=NODE(v,adj[u],lim,B),adj[u]=A;
        nod[B]=NODE(u,adj[v],0,A),adj[v]=B;
    }
}grp;
int m,n;
int preedg[N+7],flw[N+7],vis[N+7];
int BFS(int cas){
    queue<int> que;
    que.push(1);
    flw[1]=(1<<30);
    while(!que.empty()){
        int u=que.front();que.pop();
        for(int i=grp.adj[u];i!=-1;i=grp.nod[i].nxt){
            int v=grp.nod[i].to;
            if(!grp.nod[i].lim || vis[v]==cas) continue;
            vis[v]=cas;
            preedg[v]=i;flw[v]=min(grp.nod[i].lim,flw[u]);
            if(v==n) return flw[v];
            que.push(v);
        }
    }
    return 0;
}
int EK(){
    int del,res=0,cas=0;
    while(del=BFS(++cas)){
        int pnt=n;
        while(pnt!=1){
            grp.nod[preedg[pnt]].lim-=del;
            grp.nod[grp.nod[preedg[pnt]].rev].lim+=del;
            pnt=grp.nod[grp.nod[preedg[pnt]].rev].to;
        }
        res+=del;
    }
    return res;
}
int main(){
    grp.Rebuild();
    scanf("%d%d",&m,&n);
    for(int i=0;i<m;i++){
        int u,v,lim;
        scanf("%d%d%d",&u,&v,&lim);
        grp.AddEdge(u,v,lim);
    }
    int res=EK();
    printf("%d\n",res);
    return 0;
}

---

\(\mathcal{The\ End}\)

\(\mathcal{Thanks\ For\ Reading!}\)

如果有没看懂或者有问题的，请咨询作者邮箱\(lucky\_glass@foxmail.com\)~