Ionic-wechat项目边开发边学（一）：环境搭建和创建一个项目

之前学AngularJS，教程过了一遍觉得很简单，但真正写几个Demo就错误百出，一个小小的功能要折腾很久。所以这次学Ionic，准备以开发一个项目为切入点去学，那么问题来了，开发什么项目呢？

纠结了10秒，还是模仿微信吧^_^，大体列一下要实现的功能：

1. 界面要像，呵呵
2. 聊天消息列表，查看对话内容，来了消息推送提醒
3. 通讯录展示，好友搜索，右侧字母快速索引
4. 朋友圈展示，发朋友圈消息
5. 扫一扫， 摇一摇功能
6. 设置功能，设置消息提醒方式，设置聊天背景，关于等

之前根本没接触过上层应用这块，这些功能有点够呛，希望能坚持下去，把这个项目完成好，把博客写好，与各位共勉，加油！

摘要

本篇文章主要介绍一下Ionic，开发环境的配置，以及创建并运行一个官方的example
项目地址

Ionic介绍

Ionic是一个基于Cordova漂亮，开源的前端SDK，用web技术就可以开发跨平台移动app，它支持在线拖拽生成界面（ionic creator），并可以免费下载生成的代码。更多介绍
开始之前我觉得最好具备以下几点知识：

1. HTML5，CSS3和Javascript三剑客
2. AngularJS
3. NodeJS
4. 响应式布局
5. Linux（我是ubuntu14.04）

环境搭建

安装NodeJS

1. 直接在官网下载二进制包，并解压
   $ tar -xvf node-v4.0.0-linux-x64.tar.gz
2. 增加软连接
   $ sudo ln -s ./node-v4.0.0-linux-x64/bin/node /usr/bin/node
$ sudo ln -s ./node-v4.0.0-linux-x64/bin/npm /usr/bin/npm
3. 测试
   $ npm -v
$ node -v

安装android开发环境

1. 安装JDK
2. 安装Android SDK，当然要FQ啦～
   $ tar -xvf android-sdk_r24.4.1-linux.tgz
$ cd android-sdk-linux && tools && ./android
下载API22和默认勾选的项目（下载这个貌似不要FQ，我关掉这个能全速下载）
3. 添加ANDROID_HOME和adb路径， 打开～/.profile,添加两行：
   export ANDROID_HOME=~/usr/android-sdk-linux
export PATH=$PATH:${ANDROID_HOME}/platform-tools
4. 创建一个AVD(建议使用Genymotion，原装的太太太卡)，运行./android-sdk-linux/tools/monitor
5. 安装Ant
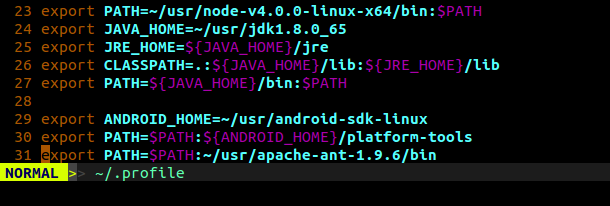
6. 给大家看一下我最后的~/.profile文件

安装cordova和Ionic

安装Cordova

$ npm install -g cordova

安装Ionic

$ sudo npm install -g ionic

创建一个项目

$ ionic start myApp tabs
创建了一个myApp项目，使用了tabs模板，另外还有两个模板blank和sidemenu

添加平台并编译(要添加ios，直接add ios)

$ cd myApp
$ ionic platform add android
$ ionic build android

在本地浏览器测试

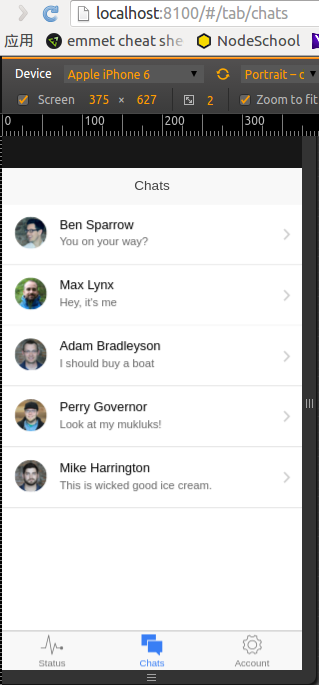
$ ionic serve
打开http://localhost:8100/

在手机测试，连上adb（或者运行Genymotion），再运行下面命令

$ ionic run android

在模拟器测试(不建议使用，AVD太太太卡)

$ ionic emulate android

ok，这篇就写到这里，下一篇项目正式开始