HohoCoder 1184 : 连通性二·边的双连通分量（+原理证明）

1184 : 连通性二·边的双连通分量

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

在基本的网络搭建完成后，学校为了方便管理还需要对所有的服务器进行编组，网络所的老师找到了小Hi和小Ho，希望他俩帮忙。

老师告诉小Hi和小Ho：根据现在网络的情况，我们要将服务器进行分组，对于同一个组的服务器，应当满足：当组内任意一个连接断开之后，不会影响组内服务器的连通性。在满足以上条件下，每个组内的服务器数量越多越好。

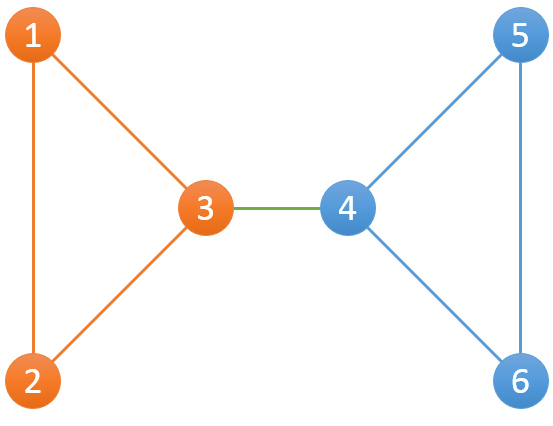
比如下面这个例子，一共有6个服务器和7条连接：

其中包含2个组，分别为{1,2,3},{4,5,6}。对{1,2,3}而言，当1-2断开后，仍然有1-3-2可以连接1和2；当2-3断开后，仍然有2-1-3可以连接2和3；当1-3断开后，仍然有1-2-3可以连接1和3。{4,5,6}这组也是一样。

老师把整个网络的情况告诉了小Hi和小Ho，小Hi和小Ho要计算出每一台服务器的分组信息。

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2个正整数，u,v。表示存在一条边(u,v)，连接了u,v两台服务器。1≤u<v≤N

保证输入所有点之间至少有一条连通路径。

输出

第1行：1个整数，表示该网络的服务器组数。

第2行：N个整数，第i个数表示第i个服务器所属组内，编号最小的服务器的编号。比如分为{1,2,3},{4,5,6}，则输出{1,1,1,4,4,4}；若分为{1,4,5},{2,3,6}则输出{1,2,2,1,1,2}

样例输入

6 7
1 2
1 3
2 3
3 4
4 5
4 6
5 6

样例输出

2
1 1 1 4 4 4

解释：

如果我们删除掉一条边之后图的连通性改变了的话，这样的边（桥）是不是一定不属于双连通子图。

对于一个无向图，当我们把图中所有的桥都去掉以后，剩下的每一个区域就是我们要求的边的双连通分量。

一：直观的做法自然先用上周的算法求出所有桥，去掉所有桥之后再做DFS求出每一个连通子图。

二：“抽象"的算法，通过Tarjan算法当中巧妙地用一个栈来统计出每一个组内的节点：

           因为low[u] == dfn[u]，对(parent[u],u)来说有dfn[u] > dfn[ parent[u] ]，因此low[u] > dfn[ parent[u]

           

           所以(parent[u],u)一定是一个桥，那么此时栈内在u之前入栈的点和u被该桥分割

       

           则u和之后入栈的节点属于同一个组

  
    将从u到栈顶所有的元素标记为一个组，并弹出这些元素。
   

#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
const int maxn=;
const int maxm=;
int low[maxn],dfn[maxn],times;
int Laxt[maxm],Next[maxm],To[maxm],cnt;
int scc_cnt,scc[maxn],Min[maxn];
vector<int>G[maxn];
int head,tail,q[maxm];
void add(int u,int v){
    Next[++cnt]=Laxt[u];
    Laxt[u]=cnt;
    To[cnt]=v;
}

void dfs(int u,int pre)
{
    q[++head]=u;
    dfn[u]=low[u]=++times;
    for(int i=Laxt[u];i;i=Next[i]){
        int v=To[i];
        if(pre==v) continue;
        if(!dfn[v]){
            dfs(v,u);
            low[u]=min(low[u],low[v]);
        }
        else low[u]=min(low[u],dfn[v]);
    }
    if(low[u]==dfn[u]){
        scc_cnt++;
        while(true){
            int v=q[head--];
            G[scc_cnt].push_back(v);
            scc[v]=scc_cnt;
            if(v==u) break;
        }
    }
}

int main()
{
     int n,m,i,j,u,v;
     scanf("%d%d",&n,&m);
     for(i=;i<=m;i++){
            scanf("%d%d",&u,&v);
            add(u,v);
            add(v,u);
     }
     dfs(,);
     for(i=;i<=scc_cnt;i++){//找最小
         int Minnum=G[i][];
         for(j=;j<G[i].size();j++){
                Minnum=min(Minnum,G[i][j]);
         }
         Min[i]=Minnum;
     }
     printf("%d\n",scc_cnt);
     for(i=;i<=n;i++)
      printf("%d ",Min[scc[i]]);
     return ;
}