最长回文子串Manacher算法模板

Manacher算法能够在O(N)的时间复杂度内得到一个字符串以任意位置为中心的回文子串。其算法的基本原理就是利用已知回文串的左半部分来推导右半部分。

首先,在字符串s中,用rad[i]表示第i个字符的回文半径,即rad[i]尽可能大,且满足:
s[i-rad[i],i-1]=s[i+1,i+rad[i]]
很明显,求出了所有的rad,就求出了所有的长度为奇数的回文子串.
至于偶数的怎么求,最后再讲.
假设现在求出了rad[1..i-1],现在要求后面的rad值,并且通过前面的操作,得知了当前字符i的rad值至少为j.现在通过试图扩大j来扫描,求出了rad[i].再假设现在有个指针k,从1循环到rad[i],试图通过某些手段来求出[i+1,i+rad[i]]的rad值.
根据定义,黑色的部分是一个回文子串,两段红色的区间全等.
因为之前已经求出了rad[i-k],所以直接用它.有3种情况:

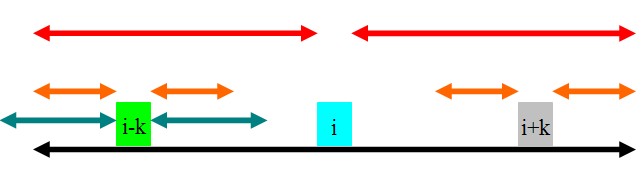
①rad[i]-k<rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分超过了黑色的部分,所以rad[i+k]肯定至少为rad[i]-k,即橙色的部分.那橙色以外的部分就不是了吗?这是肯定的.因为如果橙色以外的部分也是回文的,那么根据青色和红色部分的关系,可以证明黑色部分再往外延伸一点也是一个回文子串,这肯定不可能,因此rad[i+k]=rad[i]-k.为了方便下文,这里的rad[i+k]=rad[i]-k=min(rad[i]-k,rad[i-k]).

②rad[i]-k>rad[i-k]
如图,rad[i-k]的范围为青色.因为黑色的部分是回文的,且青色的部分在黑色的部分里面,根据定义,很容易得出:rad[i+k]=rad[i-k].为了方便下文,这里的rad[i+k]=rad[i-k]=min(rad[i]-k,rad[i-k]).

根据上面两种情况,可以得出结论:当rad[i]-k!=rad[i-k]的时候,rad[i+k]=min(rad[i]-k,rad[i-k]).
注意:当rad[i]-k==rad[i-k]的时候,就不同了,这是第三种情况:

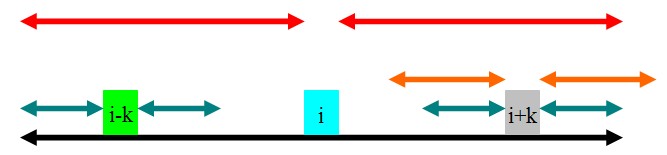
如图,通过和第一种情况对比之后会发现,因为青色的部分没有超出黑色的部分,所以即使橙色的部分全等,也无法像第一种情况一样引出矛盾,因此橙色的部分是有可能全等的,但是,根据已知的信息,我们不知道橙色的部分是多长,因此就把i指针移到i+k的位置,j=rad[i-k](因为它的rad值至少为rad[i-k]),等下次循环的时候再做了.
整个算法就这样.
至于时间复杂度为什么是O(n),我已经证明了,但很难说清楚.所以自己体会吧.
上文还留有一个问题,就是这样只能算出奇数长度的回文子串,偶数的就不行.怎么办呢?有一种直接但比较笨的方法,就是做两遍(因为两个程序是差不多的,只是rad值的意义和一些下标变了而已).但是写两个差不多的程序是很痛苦的,而且容易错.所以一种比较好的方法就是在原来的串中每两个字符之间加入一个特殊字符,再做.如:aabbaca,把它变成(#a#a#b#b#a#c#a#)，左右的括号是为了使得算法不至于越界。这样的话,无论原来的回文子串长度是偶数还是奇数,现在都变成奇数了.

#include<stdio.h>
#include<string.h>
#include<iostream>
using namespace std;
const int N=1e6+;
int rad[N<<];
char s[N],cpy[N<<];
void manacher(char *s,int len){
    for(int i=,j=,k;i<len;i+=k){
        while(s[i-j-]==s[i+j+])j++;
        rad[i]=j;
        for(k=;k<=rad[i]&&rad[i-k]!=rad[i]-k;k++){
            rad[i+k]=min(rad[i-k],rad[i]-k);
        }
        j=max(j-k,);
    }
}
void work(char *s){
    int len=strlen(s)*+;
    cpy[]='(';cpy[]='#';cpy[len-]=')';
    for(int i=,j=;s[i];i++,j+=){
        cpy[j]=s[i];
        cpy[j+]='#';
    }
    manacher(cpy,len);
    int ans=;
    for(int i=;i<len;i++){
        ans=max(ans,rad[i]);
    }
    printf("%d\n",ans);
}

　　参考文章：http://www.cnblogs.com/Lyush/p/3221503.html