CodeForces 149D Coloring Brackets

Coloring Brackets

time limit per test: 2 seconds

memory limit per test: 256 megabytes

input: standard input

output: standard output

Once Petya read a problem about a bracket sequence. He gave it much thought but didn't find a solution. Today you will face it.

You are given string s. It represents a correct bracket sequence. A correct bracket sequence is the sequence of opening ("(") and closing (")") brackets, such that it is possible to obtain a correct mathematical expression from it, inserting numbers and operators between the brackets. For example, such sequences as "(())()" and "()" are correct bracket sequences and such sequences as ")()" and "(()" are not.

In a correct bracket sequence each bracket corresponds to the matching bracket (an opening bracket corresponds to the matching closing bracket and vice versa). For example, in a bracket sequence shown of the figure below, the third bracket corresponds to the matching sixth one and the fifth bracket corresponds to the fourth one.

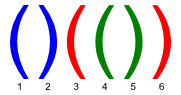
You are allowed to color some brackets in the bracket sequence so as all three conditions are fulfilled:

• Each bracket is either not colored any color, or is colored red, or is colored blue.
• For any pair of matching brackets exactly one of them is colored. In other words, for any bracket the following is true: either it or the matching bracket that corresponds to it is colored.
• No two neighboring colored brackets have the same color.

Find the number of different ways to color the bracket sequence. The ways should meet the above-given conditions. Two ways of coloring are considered different if they differ in the color of at least one bracket. As the result can be quite large, print it modulo 1000000007 (10⁹ + 7).

Input

The first line contains the single string s (2 ≤ |s| ≤ 700) which represents a correct bracket sequence.

Output

Print the only number — the number of ways to color the bracket sequence that meet the above given conditions modulo 1000000007 (10⁹ + 7).

Examples

Input

(())

Output

12

Input

(()())

Output

40

Input

()

Output

4

Note

Let's consider the first sample test. The bracket sequence from the sample can be colored, for example, as is shown on two figures below.

The two ways of coloring shown below are incorrect.

题目大意：给定一个合法的括号序列，现在要你给括号序列染色。但是必须要满足如下条件：一、一个括号可以不染色，或者染红色，或者染蓝色；二、一对匹配的括号只能有一边染色(这里的匹配是唯一的对应，而不是只要是"()"就可，下同)，且必须有一边染色；三、相邻的括号染的颜色必须不一样，但是可以都不染色。问你有多少种方案？因为方案数很大，所以结果模去1e9+7。

解题思路：容易看出这是一道DP题，并且是一道区间DP题。自己的DP很差，想了半天没想出来。于是去网上搜了一下别人的解法，瞬间恍然大悟了。设dp[l][r][x][y]表示区间[l,r]左端染的色是x，右端染的色是y的方案数，其中x，y取0,1,2，分别表示不染色，染红色，染蓝色。则该区间有三种情况，如下：

1、l+1==r，那么它们一定就是一对匹配的括号，此时，只可能有四种情况，方案数均为1，即：dp[l][r][0][1] = dp[l][r][1][0] = 1;dp[l][r][0][2] = dp[l][r][2][0] = 1;

2、l和r是一对匹配的括号，此时，区间被分为两部分，两端点以及区间[l+1,r-1]，那么我们可以先算出区间[l+1,r-1]的方案数，再由此状态转移到当前区间，两端点情况也就四种，不冲突即可转移，详见代码；

3、l和r不是一对匹配的括号，此时，区间也可被分成两部分，区间[l,mid]和区间[mid+1,r]，其中mid为l所对应与之匹配的括号，这样，一个合法的括号序列变成两个合法的括号序列，将它们分别求出方案数，再将不冲突的情况组合起来即可，详见代码。

附上AC代码：

 #include <bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 const int maxn = ;
 const int mod = ;
 ll dp[maxn][maxn][][];
 string str;
 stack<int> s;
 map<int, int> pos;

 void get_match(){
     for (int i=; i<str.size(); ++i){
         if (str[i] == '(')
             s.push(i);
         else{
             pos[i] = s.top();
             pos[s.top()] = i;
             s.pop();
         }
     }
 }

 void dfs(int l, int r){
     if (l+ == r){
         dp[l][r][][] = dp[l][r][][] = ;
         dp[l][r][][] = dp[l][r][][] = ;
         return ;
     }
     if (pos[l] == r){
         dfs(l+, r-);
         for (int i=; i<; ++i)
             for (int j=; j<; ++j){
                 if (j != )
                     dp[l][r][][] = (dp[l][r][][]+dp[l+][r-][i][j])%mod;
                 if (j != )
                     dp[l][r][][] = (dp[l][r][][]+dp[l+][r-][i][j])%mod;
                 if (i != )
                     dp[l][r][][] = (dp[l][r][][]+dp[l+][r-][i][j])%mod;
                 if (i != )
                     dp[l][r][][] = (dp[l][r][][]+dp[l+][r-][i][j])%mod;
             }
         return ;
     }
     int mid = pos[l];
     dfs(l, mid);
     dfs(mid+, r);
     for (int i=; i<; ++i)
         for (int j=; j<; ++j)
             for (int k=; k<; ++k)
                 for (int s=; s<; ++s)
                     if (!(k==&&s==) && !(k==&&s==))
                         dp[l][r][i][j] = (dp[l][r][i][j]+dp[l][mid][i][k]*dp[mid+][r][s][j])%mod;
 }

 int main(){
     ios::sync_with_stdio(false);
     cin.tie();
     cin >> str;
     get_match();
     dfs(, str.size()-);
     ll ans = ;
     for (int i=; i<; ++i)
         for (int j=; j<; ++j)
             ans = (ans+dp[][str.size()-][i][j])%mod;
     cout << ans << endl;
     return ;
 }