埃尔米特插值问题——用Python进行数值计算

　　当插值的要求涉及到对插值函数导数的要求时，普通插值问题就变为埃尔米特插值问题。拉格朗日插值和牛顿插值的要求较低，只需要插值函数的函数值在插值点与被插函数的值相等，以此来使得在其它非插值节点插值函数的值能接近被插函数。但是有时候要求会更高，不仅要插值函数与被插函数在插值节点函数值相等，而且要求它们的导数相等。

　　其实此时的情况并没有变得复杂，解决这个问题的思路与拉格朗日插值法的思路是相同的，不同点在于插值条件的约束函数增加了导数一项，原来由于0~n插值节点有n+1个插值节点，需要求出n+1个线性方程的解，(因为实打实的去求这样一个线性方程组的难度颇高)也就是需要构造一个不超过n+1-1 = n次的多项式，这里减1是因为n次多项式会解出n+1个解，还有一个常数。

　　当每一个插值节点再有一个对于导数的约束条件时，此时线性方程变成了2*（n + 1）= 2n + 2个，也就是需要构造一个不超过2n+1次的多项式。

　　构造出的埃尔米特插值函数应该是这样一个形式：

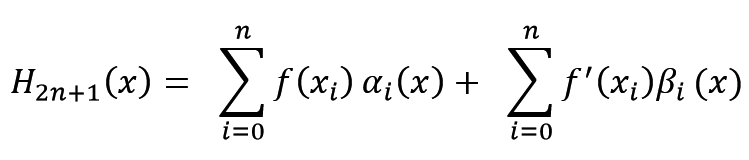
　　可以看出就是再拉格朗日插值函数的基础上添加对导数的约束。

　　构造埃尔米特插值的关键时构造基函数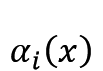与。

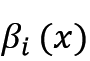　　如何构造这两个基函数我并不了解，但是可以想办法网上凑，只需要他们满足以下约束即可：

　　

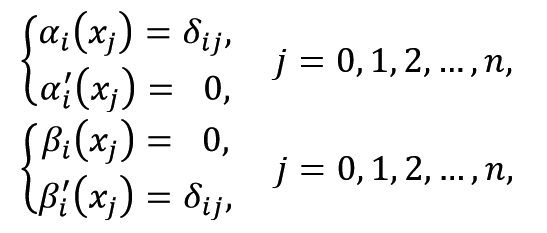
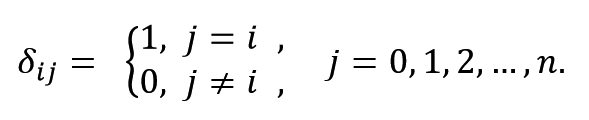
　　我在这里贴一个满足要求的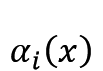与。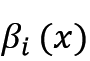

　　

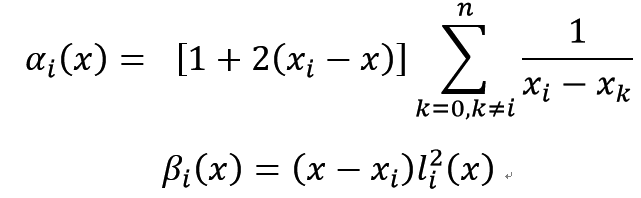
　　其中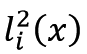为拉格朗日插值基函数的平方。

　　将以上两个基函数带入埃尔米特插值多项式便得到了插值函数。

　　开始贴代码：

　　首先贴的是拉格朗日插值基函数：

　　

"""
@brief: 获得拉格朗日插值基函数
@param: xi      xi为第i个插值节点的横坐标
@param: x_set   整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_li(xi, x_set = []):
    def li(Lx):
        W = 1; c = 1
        for each_x in x_set:
            if each_x == xi:
                continue
            W = W * (Lx - each_x)

        for each_x in x_set:
            if each_x == xi:
                continue
            c = c * (xi - each_x)

        # 这里一定要转成float类型，否则极易出现严重错误. 原因就不说了(截断误差)
        return W / float(c)
    return li

　　

　　接着根据插值节点获得埃尔米特插值多项式需要的两个基函数：

　　

"""
@brief: 获得埃尔米特插值基函数α(x)   notice: 非求导部分基函数
@param: xi      xi为第i个插值节点的横坐标
@param: x_set   整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""

def get_basis_func_alpha(xi, x_set = []):

    def basis_func_alpha(x):
        tmp_sum = 0
        for each_x in x_set:
            if each_x == xi:
                continue
            tmp_sum = tmp_sum + 1/float(xi - each_x)

        return (1 + 2*(xi-x) * tmp_sum) * ((get_li(xi, x_set))(x)) ** 2

    return basis_func_alpha

"""
@brief: 获得埃尔米特插值基函数β(x)   notice: 求导部分基函数
@param: xi      xi为第i个插值节点的横坐标
@param: x_set   整个插值节点集合
@return: 返回值为参数xi对应的插值基函数
"""
def get_basis_func_beta(xi, x_set = []):
    return lambda x : (x - xi) * ((get_li(xi, x_set))(x)) ** 2

　　最后便可以构造埃尔米特插值函数了：

　　

"""
@brief: 获得埃尔米特插值函数
@param: x       插值节点的横坐标集合
@param: fx      插值节点的纵坐标集合
@param: deriv   插值节点的导数集合
@return: 参数所指定的插值节点集合对应的插值函数
notice:
    经过对拉格朗日插值法, 牛顿插值法, 埃尔米特插值法的测试发现, 内插效果很好,
    外插基本无法使用，误差极大(不能叫误差, 应该叫错误).
"""
def get_Hermite_interpolation(x = [], fx = [], deriv = []):
    set_of_func_alpha = []  # α(x)基函数集合
    set_of_func_beta = []   # β(x)基函数集合
    for each in x:          # 获得每个插值点的基函数
        tmp_func = get_basis_func_alpha(each, x)
        set_of_func_alpha.append(tmp_func)      # 将集合x中的每个元素对应的插值基函数保存
        tmp_func = get_basis_func_beta(each, x)
        set_of_func_beta.append(tmp_func)       # 将集合x中的每个元素对应的插值基函数保存

    def Hermite_interpolation(Hx):
        result = 0
        for index in range(len(x)):
            result = result + fx[index]*set_of_func_alpha[index](Hx) + deriv[index]*set_of_func_beta[index](Hx)   #根据根据拉格朗日插值法计算Lx的值
        return result

    return Hermite_interpolation

　　　　下面看一下效果：

　　

　　对以上几个插值节点进行插值后获得了如下效果：

　　

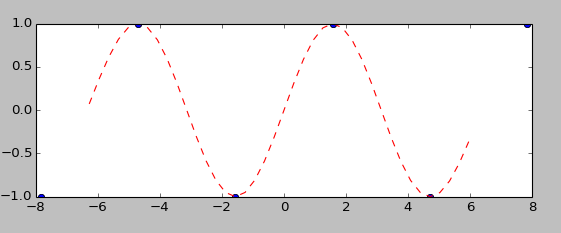
　　效果非常棒。

　　以上图像的测试代码如下：

　　

"""
demo:
"""
if __name__ == '__main__':   

    ''' 插值节点, 这里用二次函数生成插值节点，每两个节点x轴距离位10 '''
    import math
    sr_x = [(i * math.pi) + (math.pi / 2) for i in range(-3, 3)]
    sr_fx = [math.sin(i) for i in sr_x]
    deriv = [0 for i in sr_x]                           # 导数都为 0
    Hx = get_Hermite_interpolation(sr_x, sr_fx, deriv)  # 获得插值函数
    tmp_x = [i * 0.1 * math.pi for i in range(-20, 20)] # 测试用例
    tmp_y = [Hx(i) for i in tmp_x]                      # 根据插值函数获得测试用例的纵坐标

    ''' 画图 '''
    import matplotlib.pyplot as plt
    plt.figure("play")
    ax1 = plt.subplot(211)
    plt.sca(ax1)
    plt.plot(sr_x, sr_fx, linestyle = ' ', marker='o', color='b')
    plt.plot(tmp_x, tmp_y, linestyle = '--', color='r')
    plt.show()

　　通过观察以上的原理观察，实际上在以后遇到更高要求的插值问题时，比如要求插值函数与被插函数三次，四次导数相等，我们也是可以利用类似的方法，只是构造相应的基函数可能需要一番功夫，计算复杂度也会上升。