用PCA(主成分分析法)进行信号滤波

用PCA(主成分分析法)进行信号滤波

此文章从我之前的C博客上导入，代码什么的可以参考matlab官方帮助文档

现在网上大多是通过PCA对数据进行降维，其实PCA还有一个用处就是可以进行信号滤波。网上对此的介绍比较少，正好最近研究了一下，所以把自己的理解记录下来。

对于PCA原理的介绍网上已经有很多帖子，我比较喜欢的是这个：PCA的数学原理。文章把PCA降维定性和数学理解分析得生动且透彻，这里不再重复。

直接上干货吧，简单一个例子：

给定信号：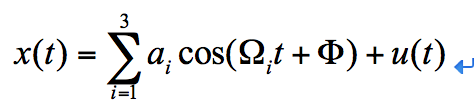

其中有用信号为三个频率不同且幅值相位不相同的余弦函数之和，我把它设为20，30，50HZ，幅值分别为1，2，3。噪声信号u(t)为高斯白噪声，我们现在要用主成分分析将高斯白噪声从x(t)中滤掉。

取100个样本x(t)，每个样本的采样点数为1000，也就是1000维（我们可以将维度理解成采样点数，至于为什么维度跟采样点数有关，也许只是正好在数学带入上呈现出相同的形式）。将这100个样本组合成100×1000的矩阵D。这100个样本中间，包含着有用信号与噪声信号两个成分。我们可以把有用信号理解为我们的主要维度A，它的“能量”是比较大的，且可以用方差表示。而噪声信号可以理解成其他维度，与有用信号彼此不是很相关，但是还是有那么一丝的相关性。我们要做的滤波，也就是去噪，就是让他们彼此之间的维度不相关，然后去掉多余的维度，只留下有用信号。

PCA的实现过程是比较规范化的：首先，求矩阵D的协方差矩阵B，协方差矩阵是个很有用的东西，他的对角线上表示的是各样本的方差，也可以理解为各维度的能量，对角线之外的元素表示不同维度之间的内积，也可以理解为相关程度。

然后，我们要讲不同维度的相关程度置0，这里可以用协方差矩阵的对角化得到。这样，我们得到的新维度两两之间就没有相关性了。然后，我们将得到的对角矩阵的特征值从大到小排列，刚才说了，对角线上特征值的大小表示相应维度的能量，表示不同维度对原信号的贡献率。

可以看到，第一主成分，也可以说在这个维度下，它的贡献率（特征值、方差、能量）最高，所以我们可以把它理解为这个主成分包含最多的有用信号。而其他维度分别以很小的，彼此不相关的形式存在着，恰恰跟高斯白噪声的性质很像，所以其他主成分我们可以在滤波中把他们去掉。

这跟降维还是有一定区别的。降维是指累计贡献率达到某个阈值，将阈值之内的主成分（维度）用来还原原始信号（有用信号+噪声信号），他更多的强调一种信号的降维还原。而滤波主要是将原来与有用信号中不相关的部分滤掉，不是一种单纯的无损还原。

所以，我们取第一主成分就够了嘛，是不是！还原出来的信号如下图：

感觉还是不错的，然后我又跟FIR滤波器对比了一下，下面是他们分别的频域图：

还是可以看出明显区别的，因为FIR滤波只能滤除截止频率之外的频率分量，而PCA可以把与主成分没关系的量统统滤除。但是，PCA的局限性也就突显出来：他只能滤出与有用信号不相关的信号，对于相关或略有相关的信号，PCA显得就比较吃力了。