LeetCode之“动态规划”：Maximal Square && Largest Rectangle in Histogram && Maximal Rectangle

　 1. Maximal Square

　　题目链接

　　题目要求：　

　　Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.

　　For example, given the following matrix:

　　Return 4.

　　在GeeksforGeeks有一个解决该问题的方法：

1) Construct a sum matrix S[R][C] for the given M[R][C].
     a) Copy first row and first columns as it is from M[][] to S[][]
     b) For other entries, use following expressions to construct S[][]
         If M[i][j] is 1 then
            S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1
         Else /*If M[i][j] is 0*/
            S[i][j] = 0
2) Find the maximum entry in S[R][C]
3) Using the value and coordinates of maximum entry in S[i], print
   sub-matrix of M[][]

　　构造完‘和矩阵S’后，我们只需求得该矩阵的最大值就可以了。

　　为什么只需求得该最大值就可以了？而且相同的最大值可能有很多个。细想下式我们就会知道‘和矩阵S’中的每一个值表示的都是从其他节点（本结点左上）到本节点所能构成的最大正方形的边长长度。

S[i][j] = min(S[i][j-1], S[i-1][j], S[i-1][j-1]) + 1

　　具体的程序如下：

 class Solution {
 public:
     int min(const int a, const int b, const int c)
     {
         int minVal = (a < b)?a:b;
         return (minVal < c)?minVal:c;
     }

     int maximalSquare(vector<vector<char>>& matrix) {
         int rows = matrix.size();
         if(rows == )
             return ;

         int cols = matrix[].size();
         if(cols == )
             return ;

         int maxEdge = ;
         vector<vector<int> > sum(rows, vector<int>(cols, ));
         for(int i = ; i < rows; i++)
         {
             if(matrix[i][] == '')
             {
                 sum[i][] = ;
                 maxEdge = ;
             }
         }

         for(int j = ; j < cols; j++)
         {
             if(matrix[][j] == '')
             {
                 sum[][j] = ;
                 maxEdge = ;
             }
         }

         for(int i = ; i < rows; i++)
             for(int j = ; j < cols; j++)
             {
                 if(matrix[i][j] == '')
                     sum[i][j] = ;
                 else
                     sum[i][j] = min(sum[i-][j-], sum[i-][j], sum[i][j-]) + ;

                 if(maxEdge < sum[i][j])
                     maxEdge = sum[i][j];
             }

         return maxEdge * maxEdge;
     }
 };

　 2.  Largest Rectangle in Histogram

　　题目链接

　　题目要求：

　　Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

　　

　　Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

　　

　　The largest rectangle is shown in the shaded area, which has area = 10 unit.

　　For example,
　　Given height = [2,1,5,6,2,3],
　　return 10.

　　这道题目实际上跟动态规划没有什么关系，之所以将其放在这里是因为其跟下一道题关系很大。该题解法参考自一博文，程序如下：

 class Solution {
 public:
     int largestRectangleArea(vector<int>& height) {
         vector<int> s;

         int sz = height.size();
         height.resize(++sz);

         int maxArea = ;
         int i = ;
         while(i < sz)
         {
             if(s.empty() || height[i] >= height[s.back()])
             {
                 s.push_back(i);
                 i++;
             }
             else
             {
                 int t = s.back();
                 s.pop_back();
                 maxArea = max(maxArea, height[t] * (s.empty() ? i : i - s.back() - ));
             }
         }

         return maxArea;
     }
 };

　　该博文还照题目要求中的例子[2，1，5，6，2，3]解析了这个函数：

　　首先，如果栈是空的，那么索引i入栈。那么第一个i=0就进去吧。注意栈内保存的是索引，不是高度。然后i++。

　　

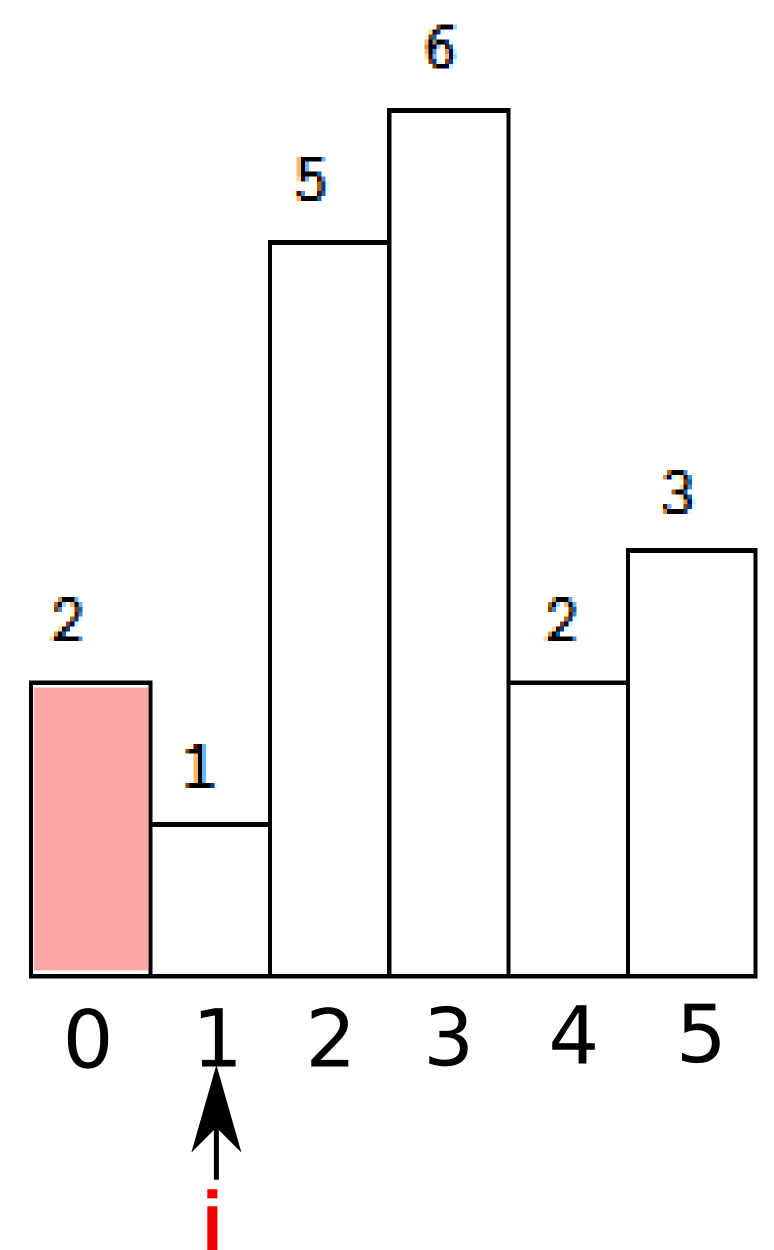
　　然后继续，当i=1的时候，发现h[i]小于了栈内的元素，于是出栈。（由此可以想到，哦，看来stack里面只存放单调递增的索引）

　　这时候stack为空，所以面积的计算是h[t] * i.t是刚刚弹出的stack顶元素。也就是蓝色部分的面积。

　　

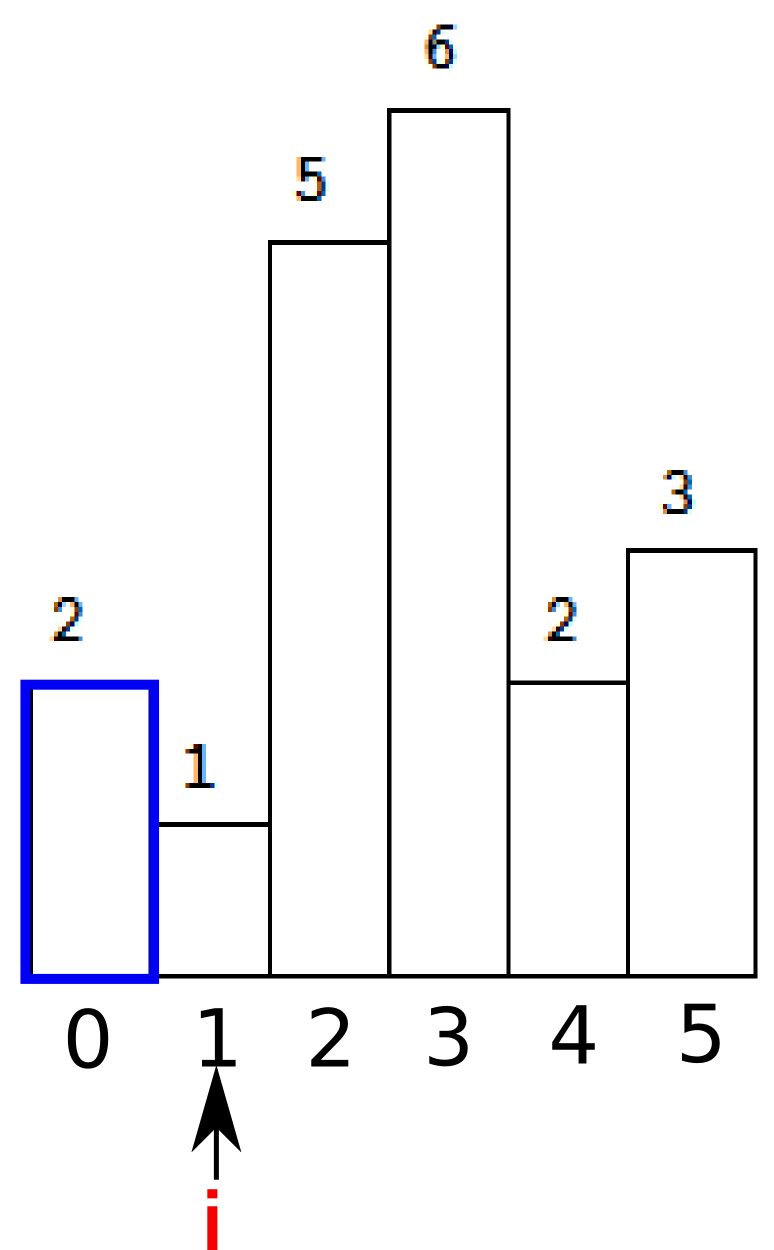
　　继续。这时候stack为空了，继续入栈。注意到只要是连续递增的序列，我们都要keep pushing，直到我们遇到了i=4，h[i]=2小于了栈顶的元素。

　　

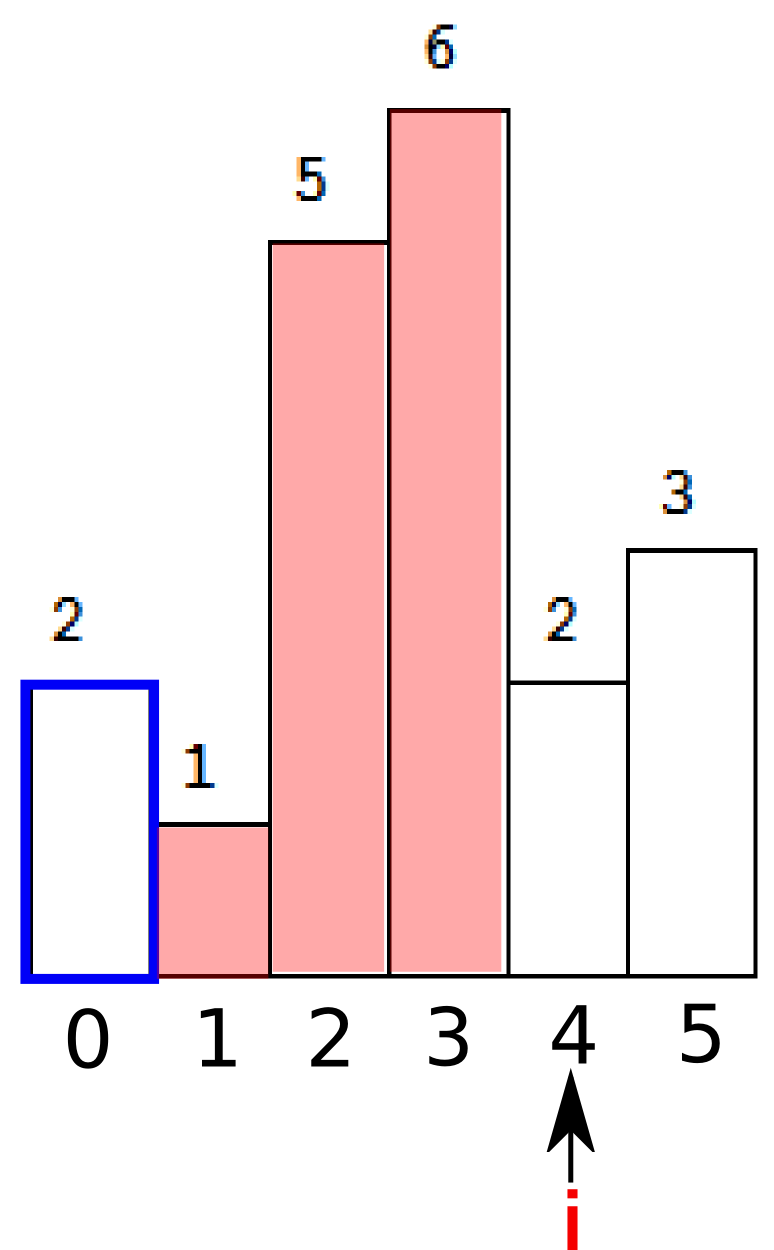
　　这时候开始计算矩形面积。首先弹出栈顶元素，t=3。即下图绿色部分。

　　

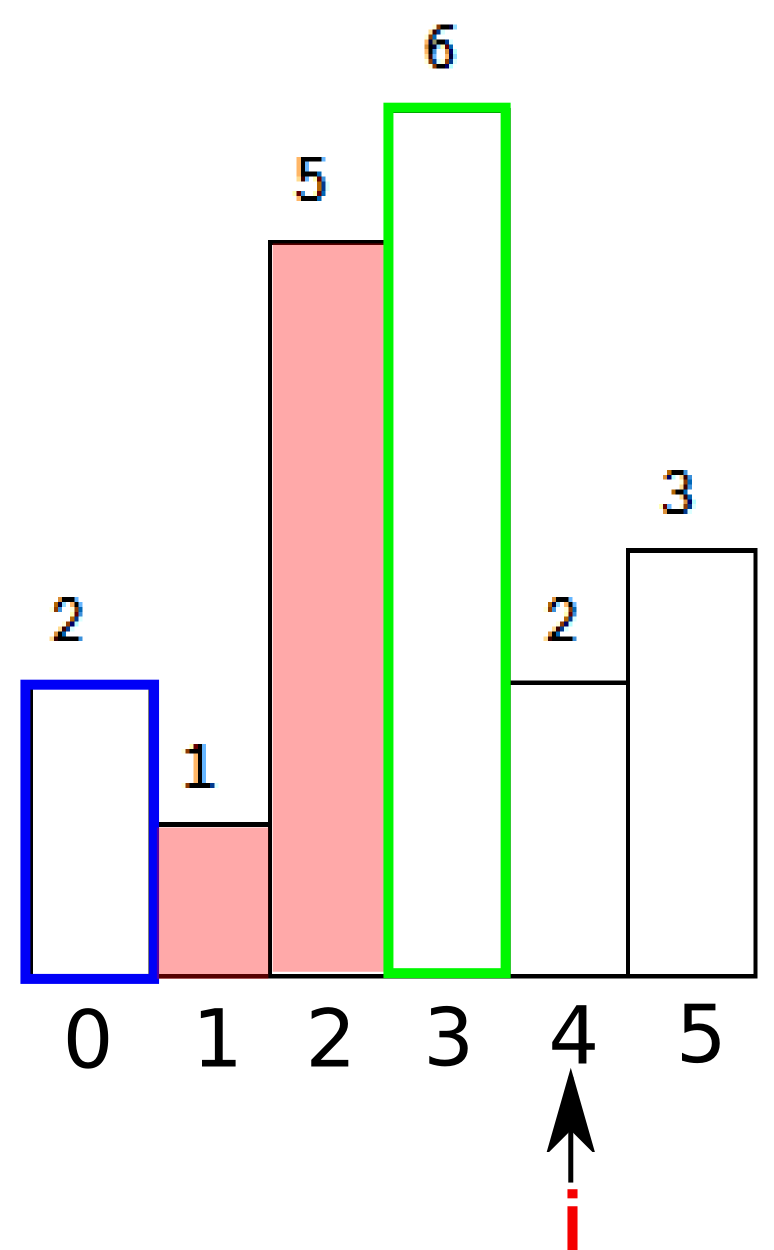
　　接下来注意到栈顶的（索引指向的）元素还是大于当前i指向的元素，于是出栈，并继续计算面积，桃红色部分。

　　

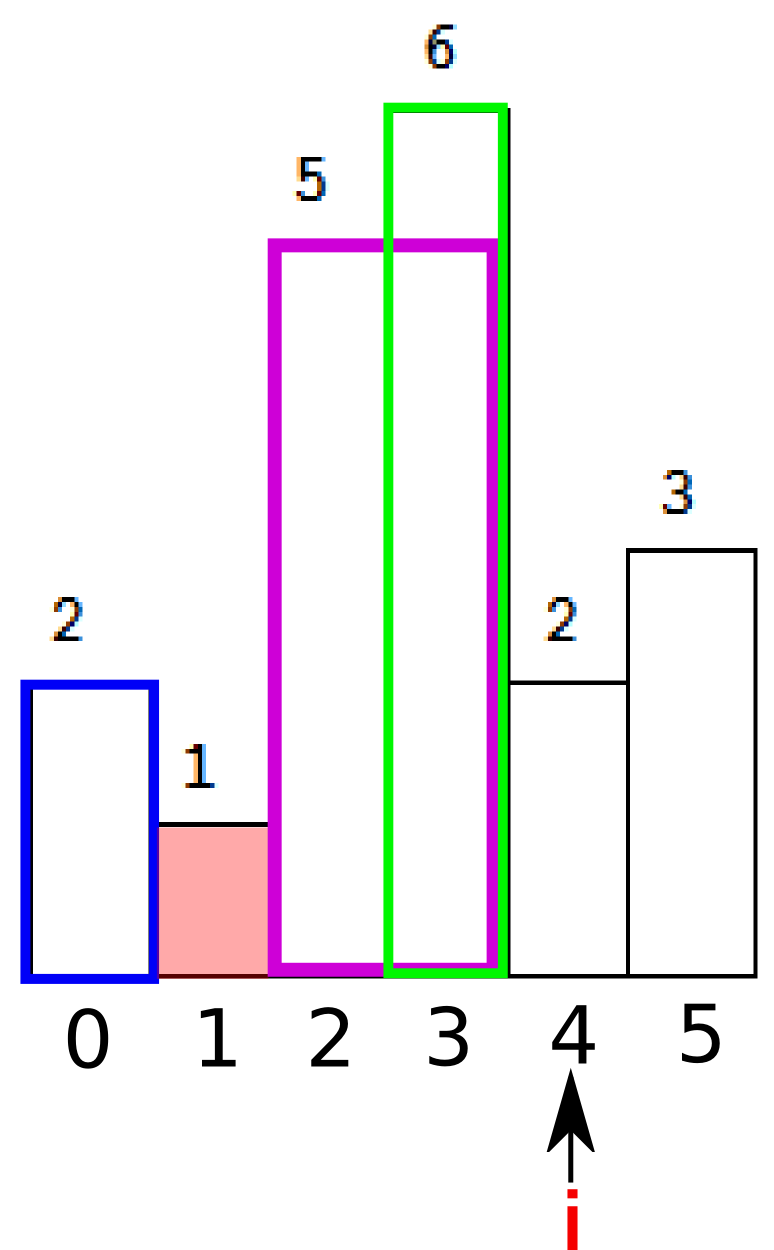
　　最后，栈顶的（索引指向的）元素大于了当前i指向的元素，循环继续，入栈并推动i前进。直到我们再次遇到下降的元素，也就是我们最后人为添加的dummy元素0.

　　

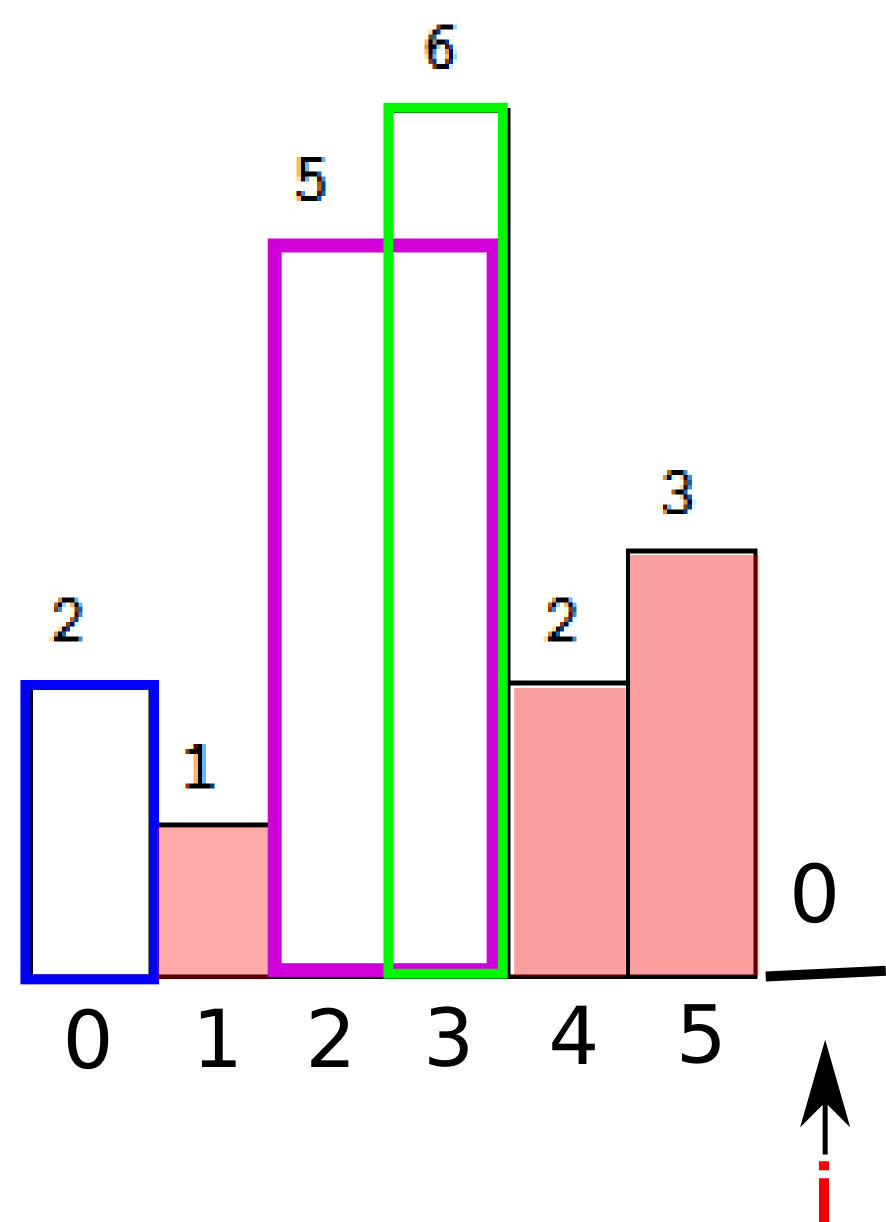
　　同理，我们计算栈内的面积。由于当前i是最小元素，所以所有的栈内元素都要被弹出并参与面积计算。

　　

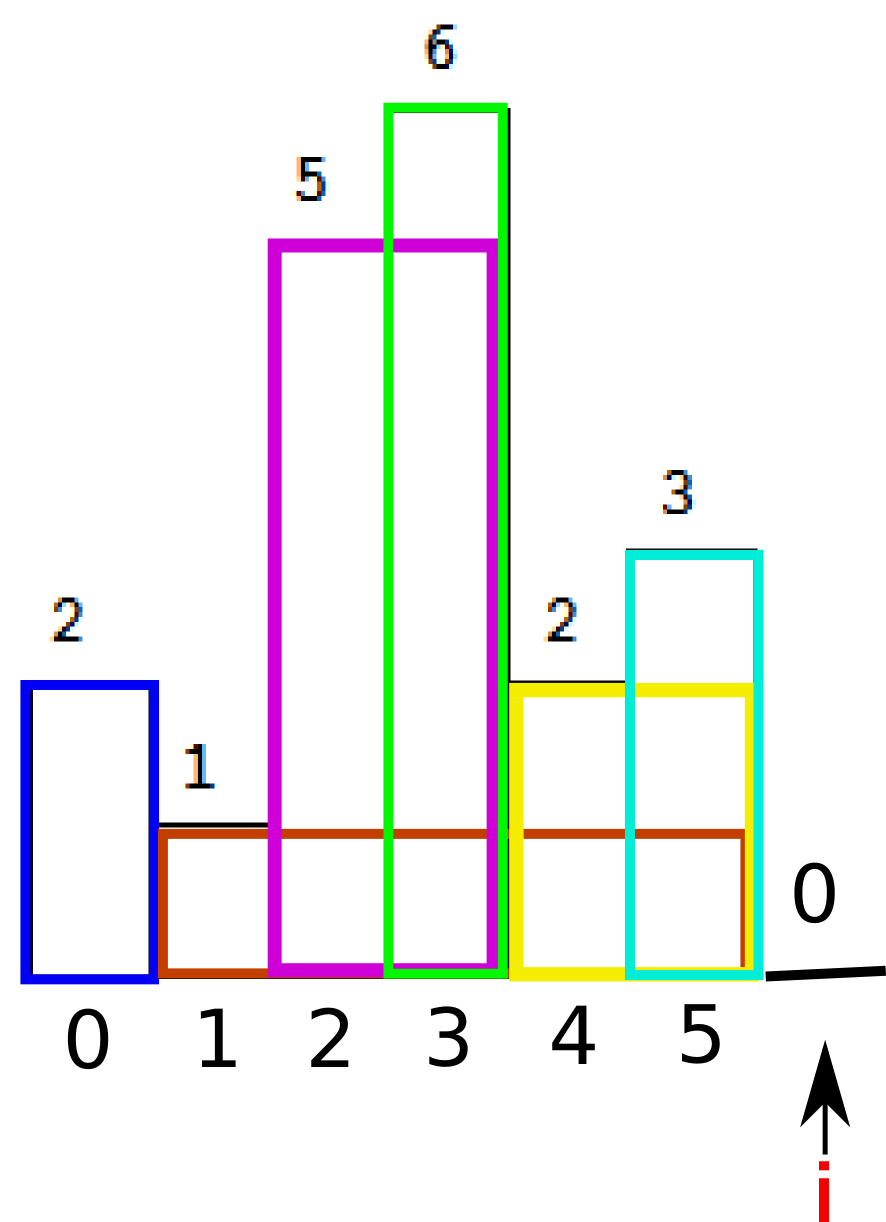
　　注意我们在计算面积的时候已经更新过了maxArea。

　　总结下，我们可以看到，stack中总是保持递增的元素的索引，然后当遇到较小的元素后，依次出栈并计算栈中bar能围成的面积，直到栈中元素小于当前元素。

　 3. Maximal Rectangle

　　题目链接

　　题目要求：

　　Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing all ones and return its area.

　　这道题的解决方法可以借鉴上题求直方图最大面积的方法，即我们把每一列当作直方图的每一列，输入则是每一列连续的‘1’的个数，具体程序如下：

 class Solution {
 public:
     int largestRectangleArea(vector<int>& height) {
         vector<int> s;

         int sz = height.size();
         height.resize(++sz);

         int maxArea = ;
         int i = ;
         while(i < sz)
         {
             if(s.empty() || height[i] >= height[s.back()])
             {
                 s.push_back(i);
                 i++;
             }
             else
             {
                 int t = s.back();
                 s.pop_back();
                 maxArea = max(maxArea, height[t] * (s.empty() ? i : i - s.back() - ));
             }
         }

         return maxArea;
     }

     int maximalRectangle(vector<vector<char>>& matrix) {
         int rows = matrix.size();
         if(rows == )
             return ;
         int cols = matrix[].size();

         vector<vector<int> > height(rows, vector<int>(cols, ));
         for(int i = ; i < rows; i++)
             for(int j = ; j < cols; j++)
             {
                 if(matrix[i][j] != '')
                     height[i][j] = (i == ) ?  : height[i-][j] + ;
             }

         int maxArea = ;
         for(int i = ; i < rows; i++)
             maxArea = max(maxArea, largestRectangleArea(height[i]));

         return maxArea;
     }
 };