Python进制转换format格式化

进制转换：先介绍用传统数学方法，再介绍用python内置方法

---

二进制转十进制：

1101 转为十进制 1*2^(4-1)+1*2^(3-1)+0*2^(2-1)+1*2^(1-1) 即各个位拆开，乘以2的（位数-1）次方，结果为13

>>> int('1101',2)
13
>>> int('0o226',8)   #00226 0：阿拉伯数字零   o：小写英文字母 o    226：八进制数
150
>>> int('0x96',16)
150

同理可得：把八进制、十六进制数按权展开、相加即得十进制数。

十进制转二进制：

比如13 用13除以2，得到的商再除以2 直到除到1，然后记录每次得到的余数， 从后往前读，即为 1101

同理可得，十进制转八进制或者十六进制按照除8或者16取余，直到商为0为止，再从最后一位读到第一位

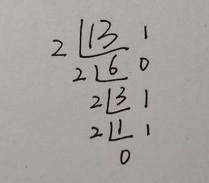
>>> bin(13)
'0b1101'

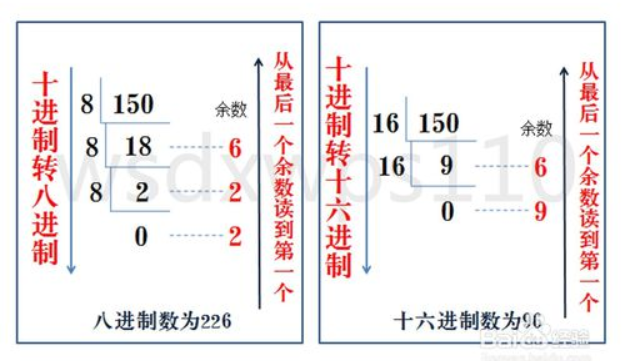
十进制转成八进制和十六进制

'{0:x}'.format(20)                转换成十六进制

'{0:o}'.format(20)                转换成八进制

进制转换的时候用{0:进制}

八进制转为二进制：

比如八进制数 (37)8

拆开 3   7     

3用二进制表示为 11                           

7用二进制表示为 111                       

合起来 即为 11 111

同理 十六进制转二进制

>>> bin(0o37)    #0o37   0：阿拉伯数字0   o：八进制表示
'0b11111'
>>> bin(0x33)
'0b110011'
>>> 

二进制转八进制：

二进制从右边数，3位3位为一组，转为十进制比如：

10 110 011 111

2     6    3      7    对应八进制就是为 （2637）8

同理十六进制，不过此时二进制应该是 从右往左边数，4位4位为一组

>>> oct(0b10110011111)
'0o2637'
>>> hex(0b10110011111)
'0x59f'
>>> 

101 1001 1111    转为十六进制对应如下：

5         9     f (15)

八进制与十六进制之间的转换有两种方法：

第一种：他们之间的转换可以先转成二进制然后再相互转换。

第二种：他们之间的转换可以先转成十进制然后再相互转换。

>>> oct(0x37)
'0o67'
>>> hex(0o67)
'0x37'

权值和第几位相关，n进制第i位的权值是n的(i-1)次方。

例如：

十进制13579，常说的百位是5，其背后的理由是10^(3-1)=100

十六进制1A2B，B所处位的权值是16^(1-1)=1（即个位），1所处位的权值是16^(4-1)=4096

 

对于多位数，处在某一位上的“l”所表示的数值的大小，称为该位的位权。例如十进制第2位的位权为10，第3位的位权为100；而二进制第2位的位权为2，第3位的位权为4，对于 N进制数，整数部分第 i位的位权为N^(i-1)，而小数部分第j位的位权为N^-j。