FFT-Matlab初步实现

/****************************************************/

/****************************************************/

/****************************************************/

下面是具体说明

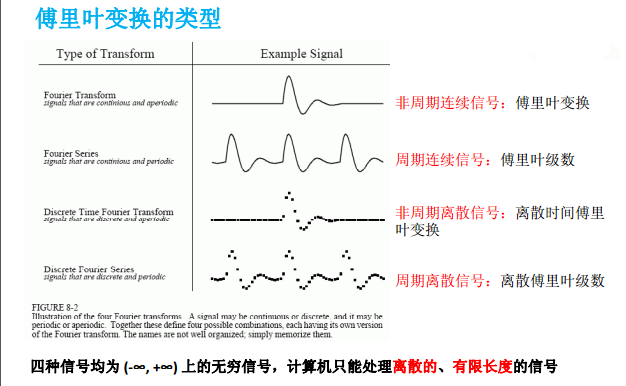
1、FFT：频谱关于中间位置对称，只需要观察  0:1：N/2（这N/2+1个点）（时域采集N个点，频域只需要观察N/2+1个点）

2、MATLAB中FFT的频谱，应该看幅值

3、X轴频率点的设置：采样频率为Fs,频谱图显示的最高频率为Fs/2（采样定理）

：X轴频率点：（0:1：N/2）*Fs/N

4、复数幅值修正

5、

/****************************************************/

/****************************************************/

/****************************************************/

栗子及实践部分

一、信号

%% FFT
clear;clc;close all
Fs=1000;    % 采集频率
T=1/Fs;     % 采集时间间隔
N=2000;     % 采集信号的长度--采样点数
f1=33;      % 第一个余弦信号的频率
f2=200;     % 第二个余弦信号的频率

t=(0:1:N-1)*T;  % 定义整个采集时间点
t=t';           % 转置成列向量

y=1.2+2.7*cos(2*pi*f1*t+pi/4)+5*cos(2*pi*f2*t+pi/6);  % 时域信号

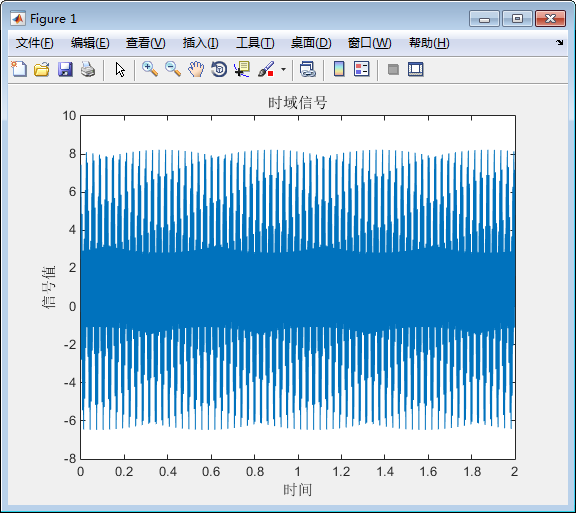
二、绘制时域信号

%% 绘制时域信号
figure
plot(t,y)
xlabel('时间')
ylabel('信号值')
title('时域信号')

　　

　　

三、FFT变换、并绘制-幅值、实部、虚部

%% fft变换
Y=fft(y);    % Y为fft变换的结果，为复数向量
A=abs(Y);    % 复数的幅值（模）
RE=real(Y);  % 复数的实部
IM=imag(Y);  % 复数的虚部

%% 绘制fft变换结果（幅值，实部，虚部）
figure
subplot(3,1,1)
plot(0:1:N-1,A)
xlabel('序号 0 ~ N-1')
ylabel('幅值')
grid on

%% 频域只读取0:1:N/2
subplot(3,1,2)
plot(0:1:N-1,RE)
xlabel('序号 0 ~ N-1')
ylabel('实部')
grid on

subplot(3,1,3)
plot(0:1:N-1,IM)
xlabel('序号 0 ~ N-1')
ylabel('虚部')
grid on

　　

　　

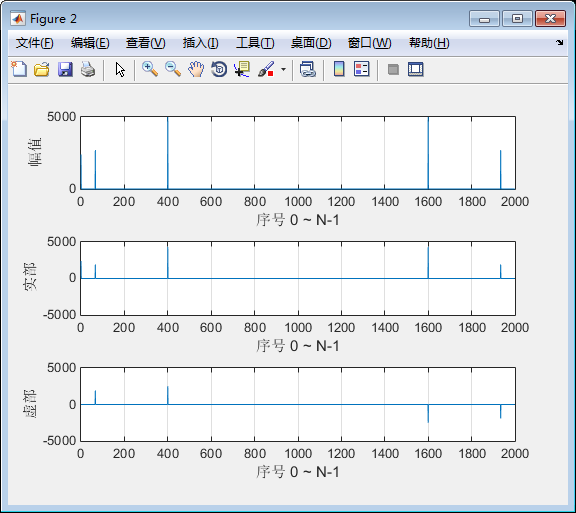
可以看出频域中的点关于（N/2）对称，所以只需要观察（0:1：N/2）

四、更改相位

 

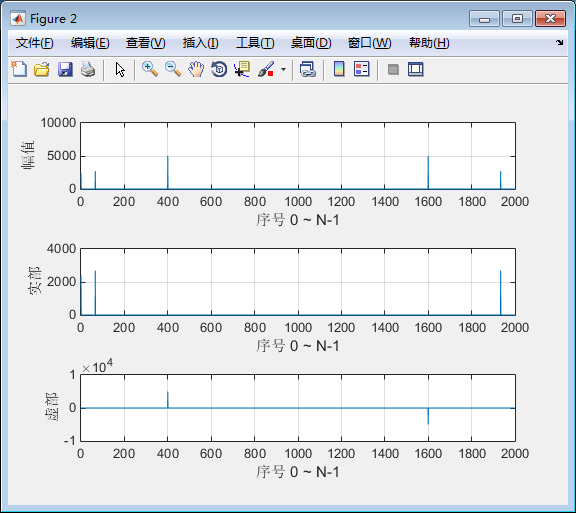
幅值不受影响，但实部或虚部的值，会出现0的情况==>看MATLAB中FFT的频谱，应该看幅值

绘制半谱图（幅值的）后--我们发现-幅值-相位-频率---均和时域对应不上。

==>进行幅值-修正

五、进行幅值-修正--并绘制图形

%% fft变换
Y=fft(y);          % Y为fft变换结果，复数向量
Y=Y(1:N/2+1);      % 只看变换结果的一半即可
A=abs(Y);          % 复数的幅值（模）
f=(0:1:N/2)*Fs/N;  % 生成频率范围
f=f';              % 转置成列向量

%% 幅值修正
A_adj=zeros(N/2+1,1);
A_adj(1)=A(1)/N;        % 频率为0的位置
A_adj(end)=A(end)/N;    % 频率为Fs/2的位置
A_adj(2:end-1)=2*A(2:end-1)/N;

%% 绘制频率幅值图
figure
subplot(2,1,1)
plot(f,A_adj)
xlabel('频率 (Hz)')
ylabel('幅值 (修正后)')
title('FFT变换幅值图')
grid on

%% 绘制频谱相位图
subplot(2,1,2)
phase_angle=angle(Y);   % angle函数的返回结果为弧度
phase_angle=rad2deg(phase_angle);
plot(f,phase_angle)
xlabel('频率 (Hz)')
ylabel('相位角 (degree)')
title('FFT变换相位图')
grid on

　　

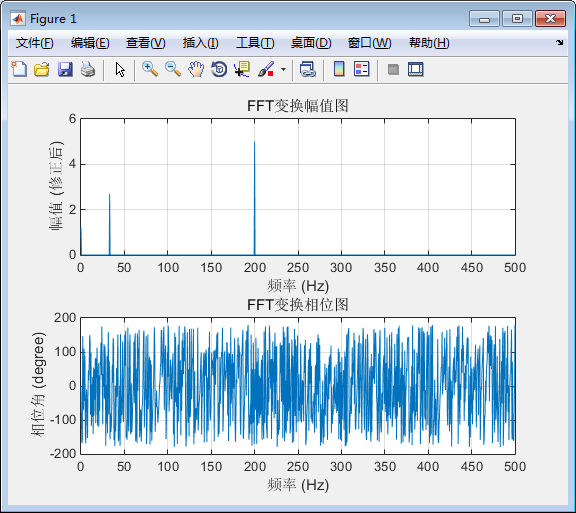
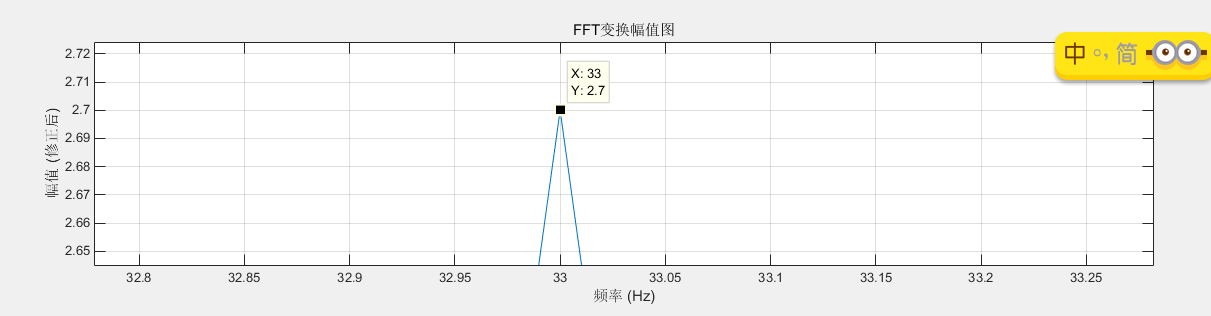
放大后可以看到，此时，幅值-频率都和时域一致

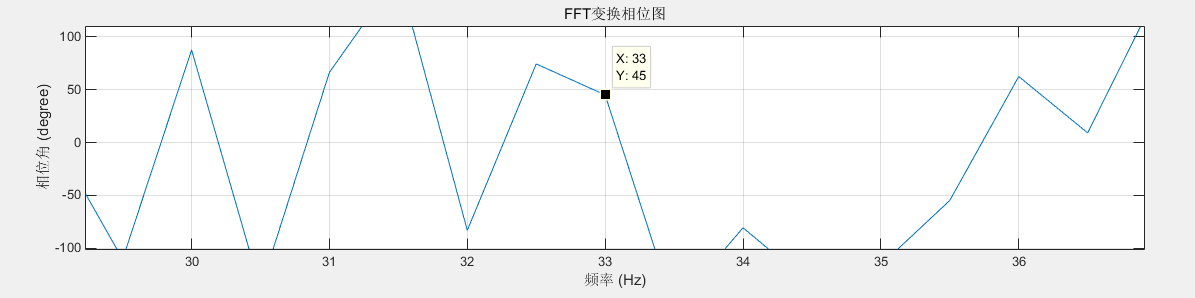
此时FFT的相位图是杂乱无章的--不用担心，没有频率处的相位是无意义的--我们只需要放大看各个（实际存在的）频率点的相位即可

可以看到--f1=33Hz处为45度，即pi/4--是正确的

六、实际操作：请分析一个未知的采集信号 (example.mat)，并确定该采集信号的频率成分。其中， 信号的采集频率 Fs = 2500 Hz

代码

clear;clc;close all
load('example')
Fs=2500;      % 采集频率
T=1/Fs;       % 采集时间间隔
N=length(y);  % 采集信号的长度

t=(0:1:N-1)*T;   % 定义整个采集时间点
t=t';            % 转置成列向量

% 绘制时域信号
figure
plot(t,y)
xlabel('时间')
ylabel('信号值')
title('时域信号')

% fft变换
Y=fft(y);          % Y为fft变换结果，复数向量
Y=Y(1:N/2+1);      % 只看变换结果的一半即可
A=abs(Y);          % 复数的幅值（模）
f=(0:1:N/2)*Fs/N;  % 生成频率范围
f=f';              % 转置成列向量

% 幅值修正
A_adj=zeros(N/2+1,1);
A_adj(1)=A(1)/N;       % 频率为0的位置
A_adj(end)=A(end)/N;   % 频率为Fs/2的位置
A_adj(2:end-1)=2*A(2:end-1)/N;

% 绘制频率幅值图
figure
subplot(2,1,1)
plot(f,A_adj)
xlabel('频率 (Hz)')
ylabel('幅值 (修正后)')
title('FFT变换幅值图')
grid on

% 绘制频谱相位图
subplot(2,1,2)
phase_angle=angle(Y);    % angle函数的返回结果为弧度
phase_angle=rad2deg(phase_angle);
plot(f,phase_angle)
xlabel('频率 (Hz)')
ylabel('相位角 (degree)')
title('FFT变换相位图')
grid on

　　

全部代码下载地址