基于CentOS6.8版本配置真实域名的方法
前言:审核了15天的时间终于审核下来了,但是结果发现配置域名掉坑了,记录一下
(一)首先配置域名三步走
1.先到域名商网站解析你你的域名(我的是百度云)
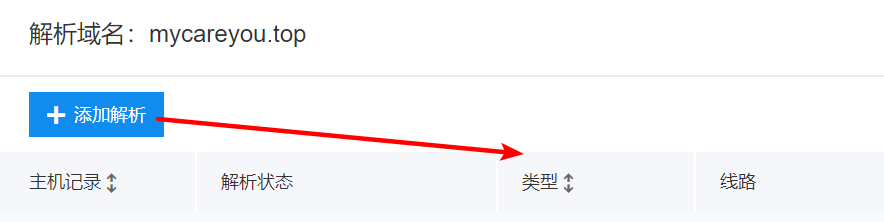
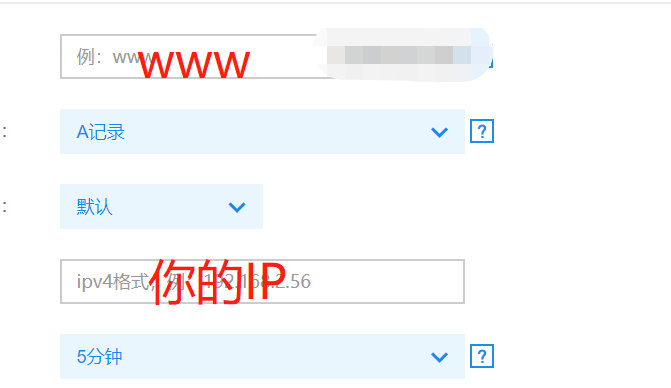
2.接着修改linux的host指向
例如: 192.168.56.14 www.myxxx(注册的域名)
3.修改httpd-vhosts.conf文件的指向
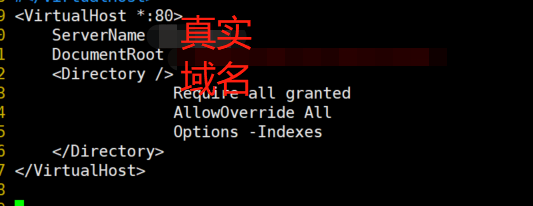
最后就可以根据你的域名去访问你的指向了
基于CentOS6.8版本配置真实域名的方法的更多相关文章
- win7下IIS配置以及域名映射方法
win7下IIS配置以及域名映射方法 第一步:打开控制面板,选择程序与功能,如下图: 第二步:双击打开程序与功能面板,如下图: 第三步:打开”打开或关闭windows功能”(红线圈起来的地方),如下图 ...
- nginx配置多域名映射方法(本地hosts)
本地测试网站的时候如果不想用localhost/xxxx的形式访问,可能就需要修改hosts文件来映射了,但是一个网站还好,假如有多个网站的话就不行了. 这时就需要配置多域名映射 比如hosts中配置 ...
- 基于MongoDB2.6版本配置MongoDB主从复制集群架构
1:集群环境说明:mongodb1:192.168.43.10.mongodb2:192.168.43.11.mongodb3:192.168.43.12.且基于主机名相互通信/etc/hosts文件 ...
- linux系统下,安装centos7.0系统,配置网卡出现的问题(与centos5.x、centos6.x版本,有差异)
1.新建虚拟机时,自己下载的是centos64系统,选择系统时,默认选择centos,而未选择centos64位,导致犯了一个低级错误,导致后面网卡安装一直有问题 2.查看ip命令与centos5.x ...
- 【Azure 环境】基于Azure搭建企业级内部站点, 配置私有域名访问的详细教程 (含演示动画)
前言 在Azure中,可以通过App Service快速部署,构建自定义站点(PaaS服务).默认情况下,这些站点被访问URL都是面向公网,通过公网进行解析.为了最好的安全保障,是否可以有一种功能实现 ...
- 基于CentOS6.5下Suricata(一款高性能的网络IDS、IPS和网络安全监控引擎)的搭建(图文详解)(博主推荐)
不多说,直接上干货! 为什么,要写这篇论文? 是因为,目前科研的我,正值研三,致力于网络安全.大数据.机器学习研究领域! 论文方向的需要,同时不局限于真实物理环境机器实验室的攻防环境.也不局限于真实物 ...
- Nginx配置同一个域名同时支持http与https两种方式访问
Nginx配置同一个域名http与https两种方式都可访问,证书是阿里云上免费申请的 server{listen 80;listen 443 ssl;ssl on;server_name 域名;in ...
- centos6.8下配置https服务器
centos6.8下配置https服务器 1.1 环境 l 系统环境:内核环境为2.6.32版本 64位的CentOS release 6.8 (Final) [root@localhost ~] ...
- windows上 nginx 配置代理服务,配置多域名,以及最简单实现跨域配置
Nginx,不用多说啦,大家都熟悉的不能再熟悉了,它是一款轻量级的高性能Web 服务器/反向代理服务器及电子邮件(IMAP/POP3)代理服务器,最近在本地研究将nginx和resin配合使用,使服务 ...
随机推荐
- 五一培训 清北学堂 DAY2
今天还是冯哲老师的讲授~~ 今日内容:简单数据结构(没看出来简单qaq) 1.搜索二叉树 前置技能 一道入门题在初学OI的时候,总会遇到这么一道题.给出N次操作,每次加入一个数,或者询问当前所有数的最 ...
- Flask 构建微电影视频网站(三)
搭建后台页面 视图函数位于admin文件夹下, app/admin/views.py 管理员登录页面搭建 视图函数 @admin.route('/') def index(): return '后台主 ...
- LOJ #2359. 「NOIP2016」天天爱跑步(倍增+线段树合并)
题意 LOJ #2359. 「NOIP2016」天天爱跑步 题解 考虑把一个玩家的路径 \((x, y)\) 拆成两条,一条是 \(x\) 到 \(lca\) ( \(x, y\) 最近公共祖先) 的 ...
- 环境变量PS1,修改命令行提示符样式
推荐模板 export PS1="\[\e[37;40m\][\[\e[31;40m\]\u\[\e[0m@\[\e[33;40m\]\H \[\e[36;40m\]\w\[\e[0m\] ...
- 【Luogu3602】Koishi Loves Segments(贪心)
[Luogu3602]Koishi Loves Segments(贪心) 题面 洛谷 题解 离散区间之后把所有的线段挂在左端点上,从左往右扫一遍. 对于当前点的限制如果不满足显然会删掉右端点最靠右的那 ...
- [bzoj2288][pojChallenge]生日礼物【贪心+堆+链表】
题目描述 ftiasch 18岁生日的时候,lqp18_31给她看了一个神奇的序列 A1, A2, -, AN. 她被允许选择不超过 M 个连续的部分作为自己的生日礼物. 自然地,ftiasch想要知 ...
- 单片机的外围功能电路 LET′S TRY“嵌入式编程”: 2 of 6
单片机的外围功能电路 LET′S TRY“嵌入式编程”: 2 of 6 本连载讲解作为嵌入式系统开发技术人员所必需具备的基础知识.这些基础知识是硬件和软件技术人员都应该掌握的共通技术知识. 上期在&l ...
- HTML 5 canvas globalCompositeOperation 属性
做一个canvas鼠标跟随动画的时候用到了,就copy w3c的解释整理一番: globalCompositeOperation 属性设置或返回如何将一个源(新的)图像绘制到目标(已有)的图像上. 源 ...
- Python中生成器generator和迭代器Iterator的使用方法
一.生成器 1. 生成器的定义 把所需要值得计算方法储存起来,不会先直接生成数值,而是等到什么时候使用什么时候生成,每次生成一个,减少计算机占用内存空间 2. 生成器的创建方式 第一种只要把一个列表生 ...
- CodeFroces-- Feel Good
题目大意:给出一段无序数组找出任意 一段区间和*这段区间的最小值 使这个值最大 栈的经典问题 用栈预处理出当前ai 为这块区间最小值的时候 的区间范围(L 和R) #include<bits/s ...
