cdqz2017-test1-数论 （BSGS + 二次剩余 + CRT）

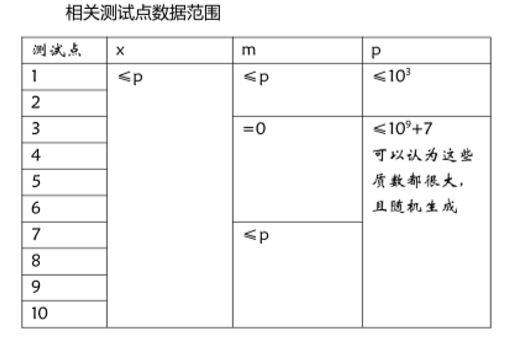
若m=0，

就是求n^2n ≡ x mod p （x--）

因为一定优解，所以x一定是p的二次剩余

令g为p的1个原根，且g^k ≡ x mod p

则k是偶数，证明k是偶数：

假设

g1^k1 ≡ x mod p

g2^k2 ≡ x mod p，k2是偶数

g1^k3 ≡ g2 mod p

那么 g1^k3k2 ≡ x ≡ g1^k1 mod p

由欧拉定理可得，k3k2 ≡ k1 mod p-1

∴ k1是偶数

所以对于任意g，k是偶数

所以等价于求 n^n ≡ g^(k/2) mod p

显然

满足 n≡ g mod  p  且  n ≡ k/2 mod p-1 的n 是一个可行解

又因为p与p-1一定互质，所以用CRT即可求得n

若m≠0

求n^2n+n^m ≡ x mod p

在上面m=0 的时候，我们是令 n ≡ g mod p

即 n^m ≡ g^m mod p

能解出合法的n的条件是 x-n^m 是p的二次剩余

所以尝试枚举g，判断x-g^m 是否是p的二次剩余

判断方法：利用欧拉准则计算勒让德符号，即 判断（x-n^m）^ ((p-1)/2)  mod p 是否等于1

如果x-g^m 是 p的二次剩余

方程变成 n^2n ≡ x-g^m mod p

令g^k ≡ x-g^m mod p

用BSGS求出一个满足上述条件的k

若k是偶数

那么方程就变成了 n^n ≡ g^(k/2) mod p

满足 n≡ g mod  p  且  n ≡ k/2 mod p-1 的n 是一个可行解

又因为p与p-1一定互质，所以用CRT即可求得n

#include<map>
#include<cmath>
#include<cstdio>
#include<iostream>

using namespace std;

map<int,int>mp;

int Pow(int a,int b,int p)
{
    int res=1;
    for(;b;a=1LL*a*a%p,b>>=1)
        if(b&1) res=1LL*res*a%p;
    return res;
}

long long Mul(long long a,int b,long long p)
{
    long long res=0;
    while(b)
    {
        if(b&1) res+=a,res%=p;
        b>>=1; a+=a; a%=p;
    }
    return res;
}        

bool Legendre(int n,int p)
{
    return Pow(n,p-1>>1,p)+1!=p;
}

int bsgs(int a,int b,int p)
{
    mp.clear();
    int m=sqrt(p);
    mp[b]=0;
    for(int i=1;i<=m;++i)
    {
        b=1LL*a*b%p;
        mp[b]=i;
    }
    int am=Pow(a,m,p);
    int mul=1;
    for(int i=1;i<=m;++i)
    {
        mul=1LL*mul*am%p;
        if(mp.find(mul)!=mp.end()) return i*m-mp[mul];
    }
    return -1;
}

int inv(int a,int p)
{
    return Pow(a,p-2,p);
}

int main()
{
    freopen("theory.in","r",stdin);
    freopen("theory.out","w",stdout);
    int x,m,p;
    scanf("%d%d%d",&x,&m,&p);
    if(p==2) printf("1");
    int y;
    long long ans;
    for(int g=1;;++g)
    {
        if(!Legendre(x-Pow(g,m,p),p)) continue;
        y=bsgs(g,(x-Pow(g,m,p)+p)%p,p);
        if(y==-1 || (y&1)) continue;
        long long P=1LL*p*(p-1);
        ans=Mul(1LL*(p-1)*inv(p-1,p)%P,g,P)+1LL*p*(y/2)%P;
        ans%=P;
        cout<<ans;
        return 0;
    }
}