CodeForces Round #548 Div2

http://codeforces.com/contest/1139

A. Even Substrings

You are given a string s=s1s2…sns=s1s2…sn of length nn, which only contains digits 11, 22, ..., 99.

A substring s[l…r]s[l…r] of ss is a string slsl+1sl+2…srslsl+1sl+2…sr. A substring s[l…r]s[l…r] of ss is called even if the number represented by it is even.

Find the number of even substrings of ss. Note, that even if some substrings are equal as strings, but have different ll and rr, they are counted as different substrings.

Input

The first line contains an integer nn (1≤n≤650001≤n≤65000) — the length of the string ss.

The second line contains a string ss of length nn. The string ss consists only of digits 11, 22, ..., 99.

Output

Print the number of even substrings of ss.

Examples

input

Copy

4
1234

output

Copy

6

input

Copy

4
2244

output

Copy

10

Note

In the first example, the [l,r][l,r] pairs corresponding to even substrings are:

• s[1…2]s[1…2]
• s[2…2]s[2…2]
• s[1…4]s[1…4]
• s[2…4]s[2…4]
• s[3…4]s[3…4]
• s[4…4]s[4…4]

In the second example, all 1010 substrings of ss are even substrings. Note, that while substrings s[1…1]s[1…1] and s[2…2]s[2…2] both define the substring "2", they are still counted as different substrings.

代码：

#include <bits/stdc++.h>
using namespace std;

int N;
string s;

int main() {
    cin >> N >> s;
    int ans = ;
    for(int i = ; i < N; i ++) {
        if((s[i] - '') %  == ) ans += (i + );
    }
    printf("%d\n", ans);
    return ;
}

B. Chocolates

You went to the store, selling nn types of chocolates. There are aiai chocolates of type ii in stock.

You have unlimited amount of cash (so you are not restricted by any prices) and want to buy as many chocolates as possible. However if you buy xixi chocolates of type ii (clearly, 0≤xi≤ai0≤xi≤ai), then for all 1≤j<i1≤j<i at least one of the following must hold:

• xj=0xj=0 (you bought zero chocolates of type jj)
• xj<xixj<xi (you bought less chocolates of type jj than of type ii)

For example, the array x=[0,0,1,2,10]x=[0,0,1,2,10] satisfies the requirement above (assuming that all ai≥xiai≥xi), while arrays x=[0,1,0]x=[0,1,0], x=[5,5]x=[5,5] and x=[3,2]x=[3,2] don't.

Calculate the maximum number of chocolates you can buy.

Input

The first line contains an integer nn (1≤n≤2⋅1051≤n≤2⋅105), denoting the number of types of chocolate.

The next line contains nn integers aiai (1≤ai≤1091≤ai≤109), denoting the number of chocolates of each type.

Output

Print the maximum number of chocolates you can buy.

Examples

input

Copy

5
1 2 1 3 6

output

Copy

10

input

Copy

5
3 2 5 4 10

output

Copy

20

input

Copy

4
1 1 1 1

output

Copy

1

Note

In the first example, it is optimal to buy: 0+0+1+3+60+0+1+3+6 chocolates.

In the second example, it is optimal to buy: 1+2+3+4+101+2+3+4+10 chocolates.

In the third example, it is optimal to buy: 0+0+0+10+0+0+1 chocolates.

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = 2e5 + ;
int N;
int a[maxn];

int main() {
    scanf("%d", &N);
    for(int i = ; i < N; i ++)
        scanf("%d", &a[i]);

    long long ans = a[N - ];
    int maxx = a[N - ];
    for(int i = N - ; i >= ; i --) {
        if(maxx == ) break;
        if(a[i] < maxx) {
            ans += a[i];
            maxx = a[i];
        } else {
            ans += (maxx - );
            maxx --;
        }

    }
    cout << ans << endl;
    //printf("%lld\n", ans);

    return ;
}

C. Edgy Trees

You are given a tree (a connected undirected graph without cycles) of nn vertices. Each of the n−1n−1 edges of the tree is colored in either black or red.

You are also given an integer kk. Consider sequences of kk vertices. Let's call a sequence [a1,a2,…,ak][a1,a2,…,ak] good if it satisfies the following criterion:

• We will walk a path (possibly visiting same edge/vertex multiple times) on the tree, starting from a1a1 and ending at akak.
• Start at a1a1, then go to a2a2 using the shortest path between a1a1 and a2a2, then go to a3a3 in a similar way, and so on, until you travel the shortest path between ak−1ak−1 and akak.
• If you walked over at least one black edge during this process, then the sequence is good.

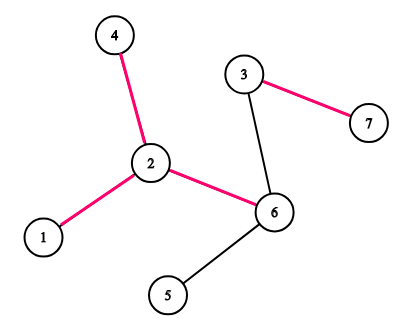
Consider the tree on the picture. If k=3k=3 then the following sequences are good: [1,4,7][1,4,7], [5,5,3][5,5,3] and [2,3,7][2,3,7]. The following sequences are not good: [1,4,6][1,4,6], [5,5,5][5,5,5], [3,7,3][3,7,3].

There are nknk sequences of vertices, count how many of them are good. Since this number can be quite large, print it modulo 109+7109+7.

Input

The first line contains two integers nn and kk (2≤n≤1052≤n≤105, 2≤k≤1002≤k≤100), the size of the tree and the length of the vertex sequence.

Each of the next n−1n−1 lines contains three integers uiui, vivi and xixi (1≤ui,vi≤n1≤ui,vi≤n, xi∈{0,1}xi∈{0,1}), where uiui and vivi denote the endpoints of the corresponding edge and xixi is the color of this edge (00 denotes red edge and 11 denotes black edge).

Output

Print the number of good sequences modulo 109+7109+7.

Examples

input

Copy

4 4
1 2 1
2 3 1
3 4 1

output

Copy

252

input

Copy

4 6
1 2 0
1 3 0
1 4 0

output

Copy

0

input

Copy

3 5
1 2 1
2 3 0

output

Copy

210

Note

In the first example, all sequences (4444) of length 44 except the following are good:

• [1,1,1,1][1,1,1,1]
• [2,2,2,2][2,2,2,2]
• [3,3,3,3][3,3,3,3]
• [4,4,4,4][4,4,4,4]

In the second example, all edges are red, hence there aren't any good sequences.

代码：

#include <bits/stdc++.h>
using namespace std;

const int mod = 1e9 + ;
const int maxn = 1e5 + ;
int N, K;
int num;
vector<int> v[maxn];
int vis[maxn];

long long Pow(long long a, long long b) {
    long long ans1 = ;

    a = a % mod;

    while(b) {
        if(b % ) {
            ans1 = (ans1 * a) % mod;
            b --;
        } else {
            a = (a * a) % mod;
            b /= ;
        }
    }
    return ans1;
}

void dfs(int st) {
    if(v[st].size() == ) {
        num ++;
        return ;
    }

    for(int i = ; i < v[st].size(); i ++) {
        if(vis[v[st][i]] == ) {
            vis[v[st][i]] = ;
            num ++;
            dfs(v[st][i]);
        }
    }
}

int main() {
    scanf("%d%d", &N, &K);
    memset(vis, , sizeof(vis));
    for(int i = ; i < N - ; i ++) {
        int st, en, col;
        scanf("%d%d%d", &st, &en, &col);
        if(col == ) {
            v[st].push_back(en);
            v[en].push_back(st);
        }
    }

    long long ans = ;
    for(int i = ; i <= N; i ++) {
        if(vis[i]) continue;
        num = ;
        dfs(i);
        ans = (ans + Pow(num, K)) % mod;
        ans %= mod;
    }

    ans = (Pow(N, K) - ans + mod) % mod;
    cout << ans << endl;

    return ;
}

E. Maximize Mex

There are nn students and mm clubs in a college. The clubs are numbered from 11 to mm. Each student has a potential pipi and is a member of the club with index cici. Initially, each student is a member of exactly one club. A technical fest starts in the college, and it will run for the next dd days. There is a coding competition every day in the technical fest.

Every day, in the morning, exactly one student of the college leaves their club. Once a student leaves their club, they will never join any club again. Every day, in the afternoon, the director of the college will select one student from each club (in case some club has no members, nobody is selected from that club) to form a team for this day's coding competition. The strength of a team is the mex of potentials of the students in the team. The director wants to know the maximum possible strength of the team for each of the coming dddays. Thus, every day the director chooses such team, that the team strength is maximized.

The mex of the multiset SS is the smallest non-negative integer that is not present in SS. For example, the mex of the {0,1,1,2,4,5,9}{0,1,1,2,4,5,9} is 33, the mex of {1,2,3}{1,2,3} is 00 and the mex of ∅∅ (empty set) is 00.

Input

The first line contains two integers nn and mm (1≤m≤n≤50001≤m≤n≤5000), the number of students and the number of clubs in college.

The second line contains nn integers p1,p2,…,pnp1,p2,…,pn (0≤pi<50000≤pi<5000), where pipi is the potential of the ii-th student.

The third line contains nn integers c1,c2,…,cnc1,c2,…,cn (1≤ci≤m1≤ci≤m), which means that ii-th student is initially a member of the club with index cici.

The fourth line contains an integer dd (1≤d≤n1≤d≤n), number of days for which the director wants to know the maximum possible strength of the team.

Each of the next dd lines contains an integer kiki (1≤ki≤n1≤ki≤n), which means that kiki-th student lefts their club on the ii-th day. It is guaranteed, that the kiki-th student has not left their club earlier.

Output

For each of the dd days, print the maximum possible strength of the team on that day.

Examples

input

Copy

5 3
0 1 2 2 0
1 2 2 3 2
5
3
2
4
5
1

output

Copy

3
1
1
1
0

input

Copy

5 3
0 1 2 2 1
1 3 2 3 2
5
4
2
3
5
1

output

Copy

3
2
2
1
0

input

Copy

5 5
0 1 2 4 5
1 2 3 4 5
4
2
3
5
4

output

Copy

1
1
1
1

Note

Consider the first example:

On the first day, student 33 leaves their club. Now, the remaining students are 11, 22, 44 and 55. We can select students 11, 22 and 44 to get maximum possible strength, which is 33. Note, that we can't select students 11, 22 and 55, as students 22 and 55 belong to the same club. Also, we can't select students 11, 33 and 44, since student 33 has left their club.

On the second day, student 22 leaves their club. Now, the remaining students are 11, 44 and 55. We can select students 11, 44 and 55 to get maximum possible strength, which is 11.

On the third day, the remaining students are 11 and 55. We can select students 11 and 55 to get maximum possible strength, which is 11.

On the fourth day, the remaining student is 11. We can select student 11 to get maximum possible strength, which is 11.

On the fifth day, no club has students and so the maximum possible strength is 00.

代码：

#include <bits/stdc++.h>
using namespace std;

const int maxn = ;
int N, M, Q;
int vis[maxn], see[maxn], sz[maxn], mp[maxn];
int p[maxn], c[maxn];
vector<int> v[maxn];
int ans = INT_MIN;
vector<int> s;

int mex(vector<int> &v) {
    int szz = v.size();
    if(szz == ) return ;
    memset(see, , sizeof(see));
    for(int i = ; i < szz; i ++)
        see[v[i]] = ;
    int temp = ;
    for(int i = ; i <= maxn; i ++) {
        if(!see[i]) {
            temp = i;
            break;
        }
    }
    return temp;
}

vector<vector<int> > out;
void dfs(int step, vector<int> &s) {
    if(step == M + ) {
        if(mex(s) >= ans)
            ans = mex(s);
        //out.push_back(s);
        return ;
    }

    if(sz[step] == ) dfs(step + , s);
    for(int i = ; i < v[step].size(); i ++) {
        if(!vis[v[step][i]]) {
            vis[v[step][i]] = ;
            s.push_back(p[v[step][i]]);
            dfs(step + , s);
            s.pop_back();
            vis[v[step][i]] = ;
        }
    }
}

int main() {
    memset(sz, , sizeof(sz));
    scanf("%d%d", &N, &M);
    for(int i = ; i <= N; i ++)
        scanf("%d", &p[i]);
    for(int i = ; i <= N; i ++) {
        scanf("%d", &c[i]);
        v[c[i]].push_back(i);
        sz[c[i]] ++;
        mp[i] = c[i];
    }
    memset(vis, , sizeof(vis));
    scanf("%d", &Q);
    while(Q --) {
        int x;
        scanf("%d", &x);
        vis[x] = ;
        sz[mp[x]] --;
        ans = INT_MIN;
        out.clear();
        vector<int> b;
        dfs(, s);
        //for(int i = 0; i < out.size(); i ++) {
            //for(int j = 0; j <out[i].size(); j ++)
              //  printf("%d ", out[i][j]);
            //printf("@@@@     %d\n", mex(out[i]));
          //  ans = max(ans, mex(out[i]));
        //}
        printf("%d\n", ans);
    }

    /*scanf("%d", &N);
    vector<int> zlr;
    for(int i = 0; i < N; i ++) {
        int x;
        scanf("%d", &x);
        zlr.push_back(x);
    }
    printf("%d\n", mex(zlr));*/
    return ;
}

//3 16 0 14 2 15 1

花了两个来小时你给我 TLE 改了无数遍还是不行 事实证明并不能暴力出奇迹 所以查了题解搞出来一个匈牙利算法也是看的一脸懵了 所以先把 TLE 的贴出来（我不管 就算 TLE 也要贴 毕竟这是我的一下午了。。。）