Tarjan求有向图强连通分量 BY：优少

Tarjan算法：一种由Robert Tarjan提出的求解有向图强连通分量的线性时间的算法。

定义给出之后，让我们进入算法的学习。。。

【情境引入】

【HAOI2006受欢迎的牛】

题目描述:

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶

牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果A喜

欢B，B喜欢C，那么A也喜欢C。牛栏里共有N 头奶牛，给定一些奶牛之间的爱慕关系，请你

算出有多少头奶牛可以当明星。

可以看出，当将每一个强连通分量视为每一个点时，受欢迎的奶牛只有可能是图中唯一的出度为零的点中的所有奶牛

这个时候，强连通分量的求得就出现了问题，这个时候，Tarjan算法应运而生

概念引入：

在有向图G中，如果两个顶点可以相互到达，则称两个顶点强连通。
如果有向图G的任意两个顶点都强连通，称G是一个强连通图。
非强连通有向图的极大强连通子图，称为强连通分量。
下图中，子图{1,2,3,4}为一个强连通分量，因为顶点1,2,3,4两两可达。{5},{6}也分别是两个强连通分量。

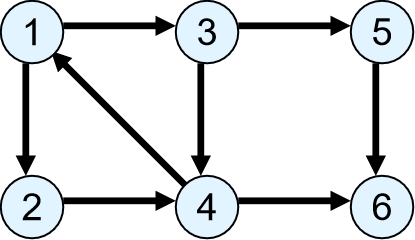
算法实现：

Tarjan算法是基于对图深度优先搜索的算法。搜索时，把当前搜索树中未处理的节点加入一个堆栈，回溯时可以判断栈顶到栈中的节点是否为一个强连通分量。

相比看完这个莫名其妙的东西很少有人能理解，那就让我们进入具体讲解：

算法准备：

dep[x]为节点x搜索的次序编号(时间戳,即搜索x的深度)。

low[x]为x或x的子树能够追溯到的最早的栈中节点的次序号。

当dep[x]=low[x]时，以x为根的搜索子树上所有节点是一个强连通分量。

4个细节

前提：搜索x->y这条边时。 初始状态deep[x]=low[x]=++tot;

如果y没有被搜过，那就入栈，深搜y，回溯时更新low[x]=min(low[x],low[y]);

如果y被搜过，并且在栈中，不再深搜y，而是直接更新low[x]=min(low[x],deep[y]);

当x所有的出边都处理完了，在这个过程中low[x]可能被多次修改

如果任然存在deep[x]==low[x],那么弹栈，直到弹出元素为x停止。那么这次弹出的所有元素就构成了一个强联通分量。

还有不太明白的同学可以手推一下这张网上疯传的tarjan讲解图（动画懒得做了）

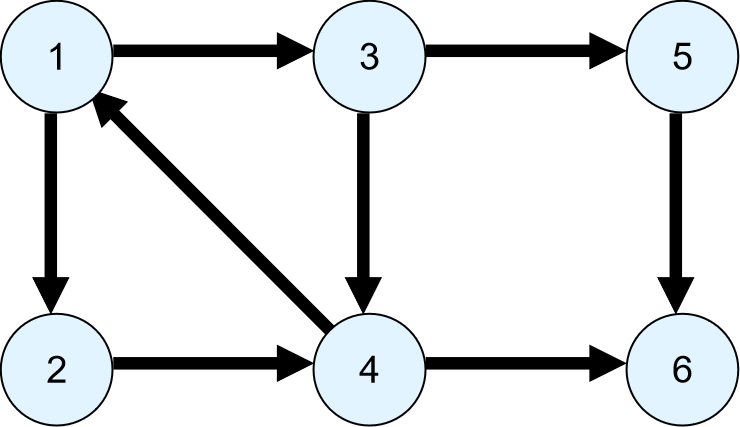
那么废话少说，上受欢迎的牛代码，没推明白的同学还可以看代码

代码如下：

#include<bits/stdc++.h>
using namespace std;
struct SYM{
    int to,next,fro;
}edge[];
int head[],n,m,tot,dep[],low[],belong[],sta[],vis[],top,num[];
void addedge(int x,int y){
    edge[++tot].to=y;
    edge[tot].fro=x;
    edge[tot].next=head[x];
    head[x]=tot;
}
int indx,cnt;
void tarjan(int x){
    dep[x]=low[x]=++indx;
    sta[++top]=x;
    vis[x]=;
    for(int i=head[x];i;i=edge[i].next){
        int to=edge[i].to;
        if(!dep[to]){
            tarjan(to);
            low[x]=min(low[x],low[to]);    //如果y没有被搜过，那就入栈，深搜y，回溯时更新low[x]=min(low[x],low[y]);
        }
        else if(vis[to]){
            low[x]=min(low[x],dep[to]);   //如果y被搜过，并且在栈中，不再深搜y，而是直接更新low[x]=min(low[x],deep[y]);
        }
    }
    if(dep[x]==low[x]){                  //如果任然存在deep[x]==low[x],那么弹栈，直到弹出元素为x停止。那么这次弹出的所有元素就构成了一个强联通分量。
        cnt++;
        int hh=-;
        while(x!=hh){
            hh=sta[top--];
            belong[hh]=cnt;
            num[cnt]++;
            vis[hh]=;
        }
    }
}
int od[];
int main(){
    int x,y;
    scanf("%d%d",&n,&m);
    for(int i=;i<=m;i++){
        scanf("%d%d",&x,&y);
        addedge(x,y);
    }
    for(int i=;i<=n;i++)
        if(!dep[i]) tarjan(i); //跑tarjan（怕是废话）
    for(int i=;i<=m;i++)
        if(belong[edge[i].fro]!=belong[edge[i].to])
           od[belong[edge[i].fro]]++; //对每一条边进行处理，如果两个端点不属于一个强连通分量则对缩出来的点之间连边
    int hhh=,ans;
    for(int i=;i<=cnt;i++){ //计算有几个出度为一的点
        if(od[i]==){
            hhh++;
            ans=i;
        }
    }
    if(hhh==) printf("%d",num[ans]);
    else printf("");
    return ;
}

其他例题：

【消息扩散】

【校园网Network of Schools】

【[USACO06JAN]牛的舞会The Cow Prom】

over~