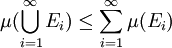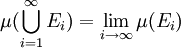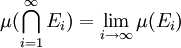测度(Measure)
测度概述
数学上,测度(Measure)是一个函数,它对一个给定集合的某些子集指定一个数,这个数可以比作大小、体积、概率等等。传统的积分是在区间上进行的,后来人们希望把积分推广到任意的集合上,就发展出测度的概念,它在数学分析和概率论有重要的地位。
测度论是实分析的一个分支,研究对象有σ代数、测度、可测函数和积分,其重要性在概率论和统计学中有所体现的。
测度的定义
形式上说,一个测度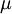 (详细的说法是可列可加的正测度)是个函数。设
(详细的说法是可列可加的正测度)是个函数。设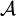 是集合
是集合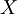 上的一个σ代数,
上的一个σ代数,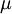 在上
在上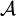 定义,于扩充区间
定义,于扩充区间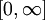 中取值,并且满足以下性质:
中取值,并且满足以下性质:
- 空集的测度为零:
-
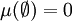 。
。
- 可数可加性,或称σ可加性:若
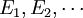 为
为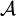 中可数个两两不交的集合的序列,则所有
中可数个两两不交的集合的序列,则所有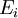 的并集的测度,等于每个
的并集的测度,等于每个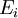 的测度之总和:
的测度之总和:
-
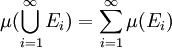 。
。
这样的三元组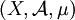 称为一个测度空间,而
称为一个测度空间,而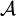 中的元素称为这个空间中的可测集。
中的元素称为这个空间中的可测集。
测度的性质
下面的一些性质可从测度的定义导出:
单调性
测度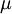 的单调性:
的单调性:
若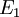 和
和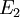 为可测集,而且
为可测集,而且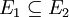 ,则
,则 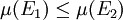 。
。
可数个可测集的并集的测度
若 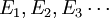 为可测集(不必是两两不交的),并且对于所有的
为可测集(不必是两两不交的),并且对于所有的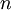 ,
, ⊆
⊆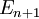 ,则集合
,则集合 的并集是可测的,且有如下不等式(「次可列可加性」):
的并集是可测的,且有如下不等式(「次可列可加性」):
以及如下极限:
可数个可测集的交集的测度
若 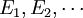 为可测集,并且对于所有的
为可测集,并且对于所有的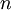 ,
,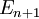 ⊆
⊆ ,则
,则 的交集是可测的。进一步说,如果至少一个
的交集是可测的。进一步说,如果至少一个 的测度有限,则有极限:
的测度有限,则有极限:
如若不假设至少一个 的测度有限,则上述性质一般不成立。例如对于每一个
的测度有限,则上述性质一般不成立。例如对于每一个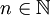 ,令
,令
这里,全部集合都具有无限测度,但它们的交集是空集。
σ有限测度
如果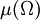 是一个有限实数(而不是
是一个有限实数(而不是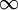 ),则测度空间
),则测度空间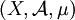 称为有限测度空间。如果
称为有限测度空间。如果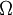 可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合
可以表示为可数个可测集的并集,而且这些可测集的测度均有限,则该测度空间称为σ有限测度空间。称测度空间中的一个集合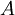 具有σ有限测度,如果
具有σ有限测度,如果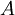 可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
可以表示为可数个可测集的并集,而且这些可测集的测度均有限。
作为例子,实数集赋以标准勒贝格测度是σ有限的,但不是有限的。为说明之,只要考虑闭区间族[k, k+1],k 取遍所有的整数;这样的区间共有可数多个,每一个的测度为1,而且并起来就是整个实数集。作为另一个例子,取实数集上的计数测度,即对实数集的每个有限子集,都把元素个数作为它的测度,至于无限子集的测度则令为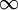 。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
。这样的测度空间就不是σ有限的,因为任何有限测度集只含有有限个点,从而,覆盖整个实数轴需要不可数个有限测度集。σ有限的测度空间有些很好的性质;从这点上说,σ有限性可以类比于拓扑空间的可分性。
完备性
一个可测集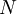 称为零测集,如果
称为零测集,如果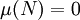 。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
。零测集的子集称为可去集,它未必是可测的,但零测集自然是可去集。如果所有的可去集都可测,则称该测度为完备测度。
一个测度可以按如下的方式延拓为完备测度:考虑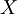 的所有这样的子集
的所有这样的子集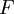 ,它与某个可测集
,它与某个可测集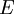 仅差一个可去集,也就是说
仅差一个可去集,也就是说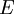 与
与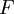 的对称差包含于一个零测集中。由这些子集
的对称差包含于一个零测集中。由这些子集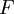 生成的σ代数,并定义
生成的σ代数,并定义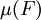 的值就等于
的值就等于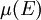 。
。
例子
下列是一些测度的例子(重要性与顺序无关)。
- 计数测度 定义为
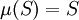 的‘元素个数’。
的‘元素个数’。 - 一维勒贝格测度 是定义在
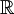 的一个含所有区间的σ代数上的、完备的、平移不变的、满足
的一个含所有区间的σ代数上的、完备的、平移不变的、满足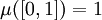 的唯一测度。
的唯一测度。 - Circular angle 测度 是旋转不变的。
- 局部紧拓扑群上的哈尔测度是勒贝格测度的一种推广,而且也有类似的刻划。
- 恆零测度 定义为
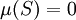 ,对任意的
,对任意的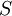 。
。 - 每一个概率空间都有一个测度,它对全空间取值为1(于是其值全部落到单位区间[0,1]中)。这就是所谓概率测度。
- 其它例子,包括:狄拉克测度、波莱尔测度、若尔当测度、遍历测度、欧拉测度、高斯测度、贝尔测度、拉东测度。
测度(Measure)的更多相关文章
- [实变函数]3.1 外测度 (outer measure)
1 并不是所有的集合都可求测度. 我们的想法是先对 $\bbR^n$ 中的任一集合定义一个``外 测度'' (outer measure), 然后再加上适当的条件 (Caratheodory 条件), ...
- 深度学习-Wasserstein GAN论文理解笔记
GAN存在问题 训练困难,G和D多次尝试没有稳定性,Loss无法知道能否优化,生成样本单一,改进方案靠暴力尝试 WGAN GAN的Loss函数选择不合适,使模型容易面临梯度消失,梯度不稳定,优化目标不 ...
- 测度论--长度是怎样炼成的[zz]
http://www.58pic.com/newpic/27882296.html http://www.58pic.com/newpic/27893137.html http://699pic.co ...
- An Introduction to Measure Theory and Probability
目录 Chapter 1 Measure spaces Chapter 2 Integration Chapter 3 Spaces of integrable functions Chapter 4 ...
- Android measure过程分析
作为一名Android开发人员,我们都知道一个View从无到有,会经历3个阶段: 1. measure/测量阶段,也就是确定某个view大小的过程: 2. layout/布局阶段,也就是确定其左上右下 ...
- \(\S1 \) Gaussian Measure and Hermite Polynomials
Define on \(\mathbb{R}^d\) the normalized Gaussian measure\[ d \gamma(x)=\frac{1}{(2\pi)^{\frac{d}{2 ...
- 通过Measure & Arrange实现UWP瀑布流布局
简介 在以XAML为主的控件布局体系中,有用于完成布局的核心步骤,分别是measure和arrange.继承体系中由UIElement类提供Measure和Arrange方法,并由其子类Framewo ...
- 普通View的measure流程
对于普通的view,其测量在ViewGroup中的measureChildWithMargins函数中调用child view的measure开始测量. 1:从measure函数开始 public f ...
- [CareerCup] 16.2 Measure Time in a Context Switch 测量上下文转换的时间
16.2 How would you measure the time spent in a context switch? 上下文转换发生在两个进程之间,比如让一个等待进程进入执行和让一个运行进程进 ...
随机推荐
- 阻塞IO与非阻塞IO、同步IO与异步IO
在学习nodejs时,了解到nodejs的一个重要特征是非阻塞IO,且nodejs中的所有IO都是异步的.既然有非阻塞IO.异步IO,那么必然就有阻塞IO.同步IO了,为了彻底搞清楚这几个概念,在网上 ...
- java并发编程(四) 线程池 & 任务执行、终止源码分析
参考文档 线程池任务执行全过程:https://blog.csdn.net/wojiaolinaaa/article/details/51345789 线程池中断:https://www.cnblog ...
- 作业:IEEE754浮点数
人工转换: 5.75转换成二进制:101.11右移2位,补0:1.0111000000000000000000000000000000000000000000000000.10000000001 16 ...
- 把ngnix注册为linux服务 将Nginx设置为linux下的服务 并设置nginx开机启动
一.创建服务脚本 vim /etc/init.d/nginx 脚本内容如下 #! /bin/sh# chkconfig: - 85 15 PATH=/usr/local/nginx/sbin/ DES ...
- jquery ajax Uncaught TypeError :Illegal invocation 报错
使用jquery ajax异步提交的时候报Uncaught TypeError :Illegal invocation错误,报错如图: 基本上,导致这个错误的原因一般有以下两点: 1.请求类型有误,如 ...
- J-CUBE Appears at AVATAR Xprize at Geneva 2019
2019年5月27日,瑞士日内瓦,Avatar Xprize发布会隆重举行.非常荣幸的是,J-CUBE也受邀参加此次大会. 关于Avatar Xprize项目的介绍 https://avatar.xp ...
- Python实用日期时间处理方法汇总
这篇文章主要介绍了Python实用日期时间处理方法汇总,本文讲解了获取当前datetime.获取当天date.获取明天/前N天.获取当天开始和结束时间(00:00:00 23:59:59).获取两个d ...
- Android最新版本号与API级别对应关系
Android版本号与API级别对应关系表 名称 版本号 API等级 发布时间 BuildVersion 2012-11-01 BuildVersionCodes.JellyBeanMr1 Jell ...
- solr的创建分片的方式
在Solr4.4之后,Solr提供了SolrCloud分布式集群的模式,它带来的主要好处是: (1)大数据量下更高的性能 (2)更好扩展性 (3)更高的可靠性 (4)更简单易用 什么时候应该使用Sol ...
- 移动端实现裁剪图片生成base64图片(可缩放)
移动端实现裁剪图片生成base64图片(可缩放)<pre><!DOCTYPE html><html lang="en"> <head> ...