洛谷P3358 最长k可重区间集问题(费用流)

题目描述

对于给定的开区间集合 I 和正整数 k，计算开区间集合 I 的最长 k可重区间集的长度。

输入输出格式

输入格式：

的第 1 行有 2 个正整数 n和 k，分别表示开区间的个数和开区间的可重迭数。接下来的 n行，每行有 2 个整数，表示开区间的左右端点坐标。

输出格式：

将计算出的最长 k可重区间集的长度输出

输入输出样例

输入样例#1： 复制

4 2
1 7
6 8
7 10
9 13 

输出样例#1： 复制

15

说明

对于100%的数据，1\le n\le 5001≤n≤500 ,1\le k\le 31≤k≤3

 

 

确实比较难想

正解有两种

借鉴一下学长的图

 

首先离散化

第一种

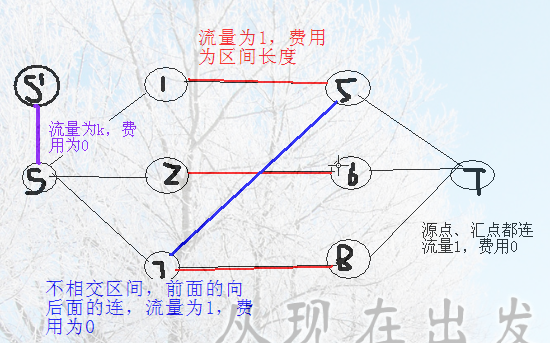
这样首先保证每个点都不会覆盖超过$k$次

那么对于一个区间后面的区间，它对这个区间内的点是没有影响的，故建一条如图所示的边

第二种

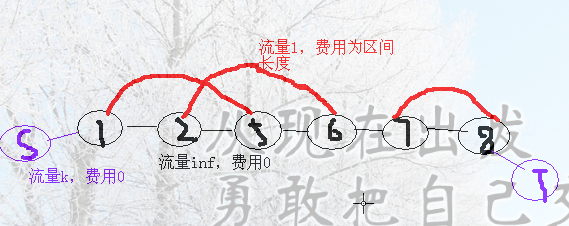
当选择了一个区间$(l,r)$后，相当于$(l,r)$这个区间内的点少了一次可以被选择的机会

所以从$l$向$r$连边

代码为第2种

#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#include<vector>
#define AddEdge(x,y,z,f) add_edge(x,y,z,f),add_edge(y,x,-z,0)
using namespace std;
const int MAXN=1e5+;
const int INF=1e6+;
inline int read()
{
    char c=getchar();int x=,f=;
    while(c<''||c>''){if(c=='-')f=-;c=getchar();}
    while(c>=''&&c<=''){x=x*+c-'';c=getchar();}
    return x*f;
}
int N,K,S,T;
int anscost=;
struct node
{
    int u,v,w,f,nxt;
}edge[MAXN];
int head[MAXN],num=;
inline void add_edge(int x,int y,int z,int f)
{
    edge[num].u=x;
    edge[num].v=y;
    edge[num].w=z;
    edge[num].f=f;
    edge[num].nxt=head[x];
    head[x]=num++;
}
int Pre[MAXN],vis[MAXN],dis[MAXN];
bool SPFA()
{
    queue<int>q;
    memset(dis,0xf,sizeof(dis));
    memset(vis,,sizeof(vis));
    dis[S]=;
    q.push(S);
    while(q.size()!=)
    {
        int p=q.front();q.pop();
        vis[p]=;
        for(int i=head[p];i!=-;i=edge[i].nxt)
        {
            if(dis[edge[i].v]>dis[p]+edge[i].w&&edge[i].f)
            {
                dis[edge[i].v]=dis[p]+edge[i].w;
                Pre[edge[i].v]=i;
                if(!vis[edge[i].v])
                    vis[edge[i].v]=,q.push(edge[i].v);
            }
        }
    }
    return dis[T]<=INF;
}
void f()
{
    int nowflow=INF;
    for(int now=T;now!=S;now=edge[Pre[now]].u)
        nowflow=min(nowflow,edge[Pre[now]].f);
    for(int now=T;now!=S;now=edge[Pre[now]].u)
        edge[Pre[now]].f-=nowflow,
        edge[Pre[now]^].f+=nowflow;
    anscost+=nowflow*dis[T];
}
void MCMF()
{
    int ans=;
    while(SPFA())
        f();
    printf("%d\n",-anscost);
}
int L[MAXN],R[MAXN],date[MAXN],tot=;
int main()
{
    #ifdef WIN32
    freopen("a.in","r",stdin);
    #else
    #endif
    memset(head,-,sizeof(head));
    N=read(),K=read();
    S=,T=*N+;
    for(int i=;i<=N;i++)
    {
        L[i]=read();R[i]=read();
        date[++tot]=L[i],
        date[++tot]=R[i];
    }
    sort(date+,date+N*+);
    int num=unique(date+,date+*N+)-date-;
    for(int i=;i<=N;i++)
        L[i]=lower_bound(date+,date+num-,L[i])-date,
        R[i]=lower_bound(date+,date+num+,R[i])-date;
    for(int i=;i<=num-;i++)
        AddEdge(i,i+,,INF);
    for(int i=;i<=N;i++)
        AddEdge(L[i],R[i],-(date[R[i]]-date[L[i]]),);
    AddEdge(S,,,K);
    AddEdge(num,T,,INF);
    MCMF();
    return ;
}