C# 优先级队列

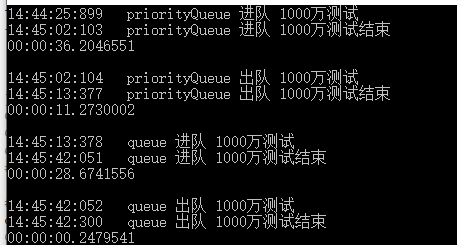
前6行是优先队列,后6行是C#原生的queue

Min Heap Priority Queue

Works with: C# version 3.0+/DotNet 3.5+

The above code is not really a true Priority Queue as it does not allow duplicate keys; also, the SortedList on which it is based does not have O(log n) insertions and removals for random data as a true Priority Queue does. The below code implements a true Min Heap Priority Queue:

namespace PriorityQ {
  using KeyT = UInt32;
  using System;
  using System.Collections.Generic;
  using System.Linq;
  class Tuple<K, V> { // for DotNet 3.5 without Tuple's
    public K Item1; public V Item2;
    public Tuple(K k, V v) { Item1 = k; Item2 = v; }
    public override string ToString() {
      return "(" + Item1.ToString() + ", " + Item2.ToString() + ")";
    }
  }
  class MinHeapPQ<V> {
    private struct HeapEntry {
      public KeyT k; public V v;
      public HeapEntry(KeyT k, V v) { this.k = k; this.v = v; }
    }
    private List<HeapEntry> pq;
    private MinHeapPQ() { this.pq = new List<HeapEntry>(); }
    ; } }
    private int sz {
      get {
        var cnt = pq.Count;
        ) ?  : cnt - ;
      }
    }
    private Tuple<KeyT, V> pkmn {
      get {
        ) return null;
        else {
          ];
          return new Tuple<KeyT, V>(mn.k, mn.v);
        }
      }
    }
    private void psh(KeyT k, V v) { // add extra very high item if none
      ) pq.Add(new HeapEntry(UInt32.MaxValue, v));
      ]); // copy bottom item...
      ; ni > ; i >>= , ni >>= ) {
        ];
        ] = t; else break;
      }
      pq[i - ] = new HeapEntry(k, v);
    }
    private void siftdown(KeyT k, V v, int ndx) {
      ; var i = ndx;
      ; ni < cnt; ni = ni + ni + ) {
        ].k;
        var nk = k;
        if (k > lk) { i = ni; nk = lk; }
        ; i = ni; }
        if (i != oi) pq[oi] = pq[i]; else break;
      }
      pq[i] = new HeapEntry(k, v);
    }
    private void rplcmin(KeyT k, V v) {
      ) siftdown(k, v, );
    }
    private void dltmin() {
      ;
      ) pq.Clear();
      else {
        var lkv = pq[lsti];
        pq.RemoveAt(lsti); siftdown(lkv.k, lkv.v, );
      }
    }
    private void reheap(int i) {
      ;
      if (lfti < sz) {
        ; reheap(lfti); reheap(rghti);
        var ckv = pq[i]; siftdown(ckv.k, ckv.v, i);
      }
    }
    private void bld(IEnumerable<Tuple<KeyT, V>> sq) {
      var sqm = from e in sq
                select new HeapEntry(e.Item1, e.Item2);
      pq = sqm.ToList<HeapEntry>();
      var sz = pq.Count;
      ) {
        ];
        pq.Add(new HeapEntry(KeyT.MaxValue, lkv.v));
        reheap();
      }
    }
    private IEnumerable<Tuple<KeyT, V>> sq() {
      return from e in pq
             where e.k != KeyT.MaxValue
             select new Tuple<KeyT, V>(e.k, e.v); }
    private void adj(Func<KeyT, V, Tuple<KeyT, V>> f) {
      ;
      ; i < cnt; ++i) {
        var e = pq[i];
        var r = f(e.k, e.v);
        pq[i] = new HeapEntry(r.Item1, r.Item2);
      }
      reheap();
    }
    public static MinHeapPQ<V> empty { get { return new MinHeapPQ<V>(); } }
    public static bool isEmpty(MinHeapPQ<V> pq) { return pq.mt; }
    public static int size(MinHeapPQ<V> pq) { return pq.sz; }
    public static Tuple<KeyT, V> peekMin(MinHeapPQ<V> pq) { return pq.pkmn; }
    public static MinHeapPQ<V> push(KeyT k, V v, MinHeapPQ<V> pq) {
      pq.psh(k, v); return pq; }
    public static MinHeapPQ<V> replaceMin(KeyT k, V v, MinHeapPQ<V> pq) {
      pq.rplcmin(k, v); return pq; }
    public static MinHeapPQ<V> deleteMin(MinHeapPQ<V> pq) { pq.dltmin(); return pq; }
    public static MinHeapPQ<V> merge(MinHeapPQ<V> pq1, MinHeapPQ<V> pq2) {
      return fromSeq(pq1.sq().Concat(pq2.sq())); }
    public static MinHeapPQ<V> adjust(Func<KeyT, V, Tuple<KeyT, V>> f, MinHeapPQ<V> pq) {
      pq.adj(f); return pq; }
    public static MinHeapPQ<V> fromSeq(IEnumerable<Tuple<KeyT, V>> sq) {
      var pq = new MinHeapPQ<V>(); pq.bld(sq); return pq; }
    public static Tuple<Tuple<KeyT, V>, MinHeapPQ<V>> popMin(MinHeapPQ<V> pq) {
      var rslt = pq.pkmn; if (rslt == null) return null;
      pq.dltmin(); return new Tuple<Tuple<KeyT, V>, MinHeapPQ<V>>(rslt, pq); }
    public static IEnumerable<Tuple<KeyT, V>> toSeq(MinHeapPQ<V> pq) {
      for (; !pq.mt; pq.dltmin()) yield return pq.pkmn; }
    public static IEnumerable<Tuple<KeyT, V>> sort(IEnumerable<Tuple<KeyT, V>> sq) {
      return toSeq(fromSeq(sq)); }
  }
}

The above class code offers a full set of static methods and properties:

 1.  "empty" to create a new empty queue,
 2.  "isEmpty" to test if a queue is empty,
 3.  "size" to get the number of elements in the queue,
 4.  "peekMin" to retrieve the lowest priority key/value pair entry as a Tuple (possibly null for empty queues),
 5.  "push" to insert an entry,
 6.  "deleteMin" to remove the lowest priority entry,
 7.  "replaceMin" to replace the lowest priority and adjust the queue according to the value (faster than a "deleteMin" followed by a "push"),
 8.  "adjust" to apply a function to every key/value entry pair and reheapify the result,
 9.  "merge" to merge two queues into a single reheapified result,
 10. "fromSeq" to build a queue from a sequence of key/value pair tuples,
 11. "popMin" which is a convenience function combining a "peekMin" with a "deleteMin", returning null if the queue is empty and a tuple of the result otherwise,
 12. "toSeq" to output an ordered sequence of the queue contents as Tuple's of the key/value pairs, and
 13. "sort" which is a convenience function combining "fromSeq" followed by "toSeq".

The first four are all O(1) and the remainder O(log n) except "adjust" and "fromSeq" are O(n), "merge" is O(m + n) where m and n are the sizes of the two queues, and "toSeq" and "sort" are O(n log n); "replaceMin" is still O(log n) but faster than a "deleteMin" followed by a "push" by a constant factor.

Note that the Key type "KeyT" is not generic in order to give better comparison efficiency than using generic comparison using the IComparible interface but can be changed to different numeric types using the "using KeyT = ???" type alias.

The above code can be tested as per the page specification by the following code:

static void Main(string[] args) {
      Tuple<uint, string>[] ins = { new Tuple<uint,string>(3u, "Clear drains"),
                                    new Tuple<uint,string>(4u, "Feed cat"),
                                    new Tuple<uint,string>(5u, "Make tea"),
                                    new Tuple<uint,string>(1u, "Solve RC tasks"),
                                    new Tuple<uint,string>(2u, "Tax return") };

      var spq = ins.Aggregate(MinHeapPQ<string>.empty, (pq, t) => MinHeapPQ<string>.push(t.Item1, t.Item2, pq));
      foreach (var e in MinHeapPQ<string>.toSeq(spq)) Console.WriteLine(e); Console.WriteLine();

      foreach (var e in MinHeapPQ<string>.sort(ins)) Console.WriteLine(e); Console.WriteLine();

      var npq = MinHeapPQ<string>.fromSeq(ins);
      foreach (var e in MinHeapPQ<string>.toSeq(MinHeapPQ<string>.merge(npq, npq)))
        Console.WriteLine(e); Console.WriteLine();

      var npq = MinHeapPQ<string>.fromSeq(ins);
      foreach (var e in MinHeapPQ<string>.toSeq(MinHeapPQ<string>.merge(npq, npq)))
        Console.WriteLine(e);

      foreach (var e in MinHeapPQ<string>.toSeq(MinHeapPQ<string>.adjust((k, v) => new Tuple<uint,string>(6u - k, v), npq)))
        Console.WriteLine(e); Console.WriteLine();
    }

It tests building the queue the slow way using repeated "push"'s - O(n log n), the faster "fromSeq" (included in the "sort") - O(n), and also tests the "merge" and "adjust" methods.

The output of the above test is as follows:

Output:

(1, Solve RC tasks)
(2, Tax return)
(3, Clear drains)
(4, Feed cat)
(5, Make tea)

(1, Solve RC tasks)
(2, Tax return)
(3, Clear drains)
(4, Feed cat)
(5, Make tea)

(1, Solve RC tasks)
(1, Solve RC tasks)
(2, Tax return)
(2, Tax return)
(3, Clear drains)
(3, Clear drains)
(4, Feed cat)
(4, Feed cat)
(5, Make tea)
(5, Make tea)

(1, Make tea)
(2, Feed cat)
(3, Clear drains)
(4, Tax return)
(5, Solve RC tasks)

再贴上自己写的一点扩展方法

    public static class MinHeapPQEX
    {
        /// <summary>
        /// 创建一个空的优先级队列O(1)
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <returns></returns>
        public static PriorityQueue<T> CreatPriorityQueue<T>()
        {
            return PriorityQueue<T>.empty;
        }

        /// <summary>
        /// 进队 O(log n)
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        /// <param name="priority"></param>
        /// <param name="model"></param>
        public static void Enqueue<T>(this PriorityQueue<T> pq, UInt32 priority, T model)
        {
            PriorityQueue<T>.push(priority, model, pq);
        }

        /// <summary>
        /// 出队  peek+delete
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        /// <returns></returns>
        public static T Dequeue<T>(this PriorityQueue<T> pq)
        {
            return PriorityQueue<T>.popMin(pq).Item1.Item2;
        }

        /// <summary>
        /// 检索,但不出队 O(1)
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        /// <returns></returns>
        public static T Peek<T>(this PriorityQueue<T> pq)
        {
            return PriorityQueue<T>.peekMin(pq).Item2;
        }

        /// <summary>
        /// 判断队列是否为空 O(1)
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        /// <returns></returns>
        public static bool IsEmpty<T>(this PriorityQueue<T> pq)
        {
            return PriorityQueue<T>.isEmpty(pq);
        }

        /// <summary>
        /// 统计 O(1)
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        /// <returns></returns>
        public static int Count<T>(this PriorityQueue<T> pq)
        {
            return PriorityQueue<T>.size(pq);
        }

        /// <summary>
        /// 删除即将出队的元素
        /// </summary>
        /// <typeparam name="T"></typeparam>
        /// <param name="pq"></param>
        public static void Delete<T>(this PriorityQueue<T> pq)
        {
            PriorityQueue<T>.deleteMin(pq);
        }
    }