A*算法的有关知识--例子:最短路径问题
前置知识
定义1,g(n)=从树根到节点n的代价。当算法处理到某个节点时,g(n)是可以精确计算的。
定义2,h*(n)=从节点n到目标节点的优化路径的代价。一般不可知。
定义3,f*(n)=g(n) + h*(n)是包含节点n的路径的最小代价。一般不可知。
定义4,h(n)=从节点n到目标节点的优化路径的估计代价。
定义5,f(n)=g(n) + h(n)是包含节点n的路径的估计最小代价。
假设,对于任意的节点n而言,已知h*(n),可以构建出一个算法直接找到最优解,即处理每一次选择时,都选择f*(n)代价最小的节点。但是,对于任意一个算法而言,h*(n)不可知,我们只能够估计h*(n)的值,这也是爬山法和Best-Frist算法中评价函数或启发式函数的作用。
算法本质
A*算法保证所估计h*(n)的值h(n)满足:h(n) ≤ h*(n)。
一旦满足这个条件,当使用使用Best-first策略搜索时,如果该方法选中的节点是目标节点,那么该节点表示的解就是当前问题的最优解。
定理1,使用Best-first策略搜索,且满足h(n) ≤ h*(n),如果算法选择的节点是目标节点, 则该节点表示的解是优化解。
证明1:只需要证明,f*(t)是最优解代价即可,n为此时可以进行扩展的所有节点,即f*(t)是{f*(n)}中的最小值。
- 由于节点t是目标节点,所以h*(t) = h(t) = 0,f(t) = f*(t) = g(t)。
- 假设:{f*(n)}中的最小值为M,M∈{f*(n)}。
- 由于 f*(t)∈{f*(n)},故而,f(t) ≥ M。
- 由于此时算法选择的节点是节点t,即在当前可以扩展的节点中,t是估计总代价最小的那一个,故而 f(t) ≤ f(n) ,而对于所有当前可以扩展的节点n而言,由于h(n) ≤ h*(n),所以 f(n) ≤ f*(n),而{f*(n)}中的最小值为M,f(t) ≤ M。
- 由 f(t) ≥ M 以及 f(t) ≤ M 可知,f(t) = M。
算法拓展
可以将A*算法的h(n)作两种极端情况的考虑。
- 对于任意的节点n,h(n) = 0,此时算法退化,每一次进行选择时,选择当前g(n)最小也就是当前路径长度最小的点。
- 对于任意的节点n,h*(n) = 0,正如本文之前提到的,直接可以选择得到,不会走其他路径。
由此,可以明确的是,尽量使得h(n)接近h*(n),越接近,算法越佳。
例子说明
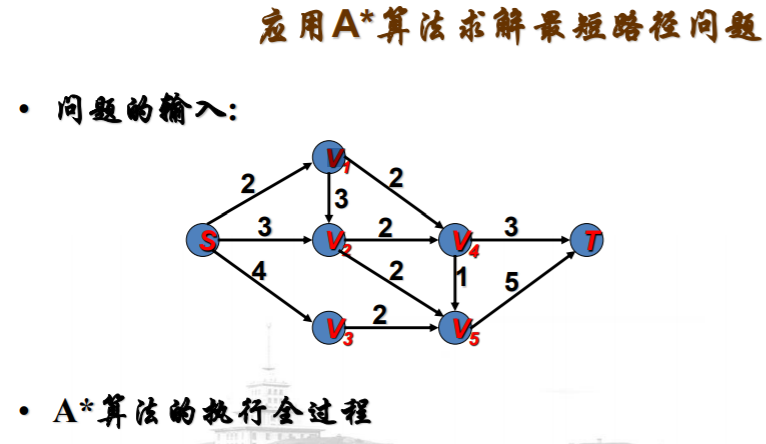

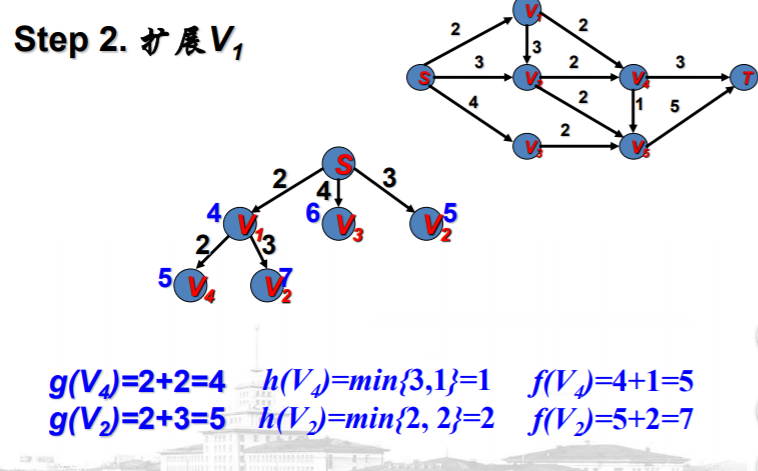
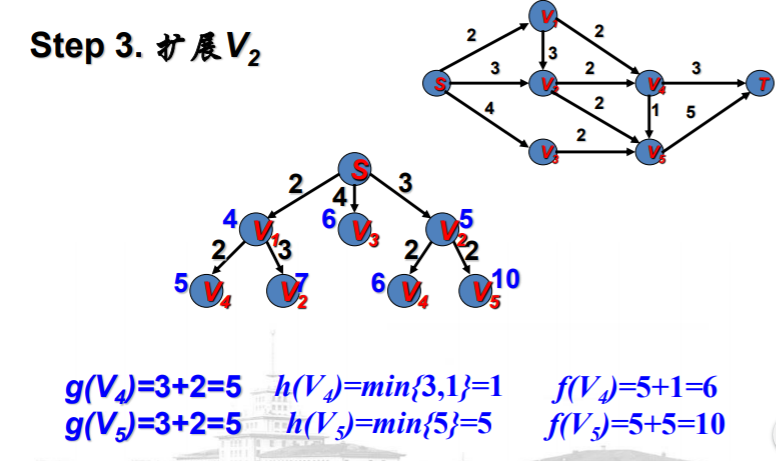
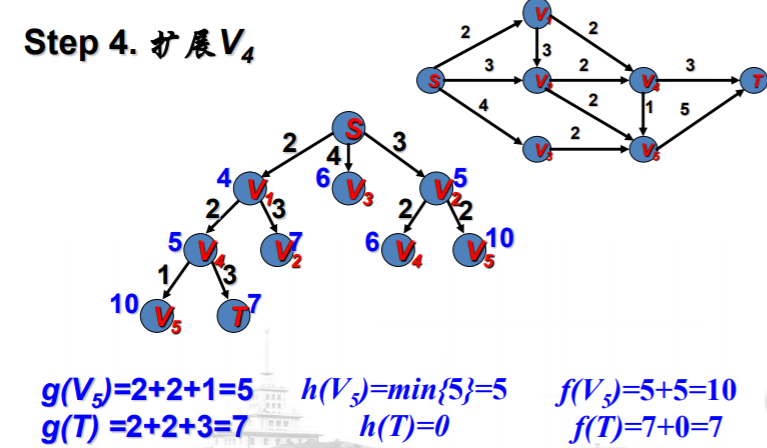
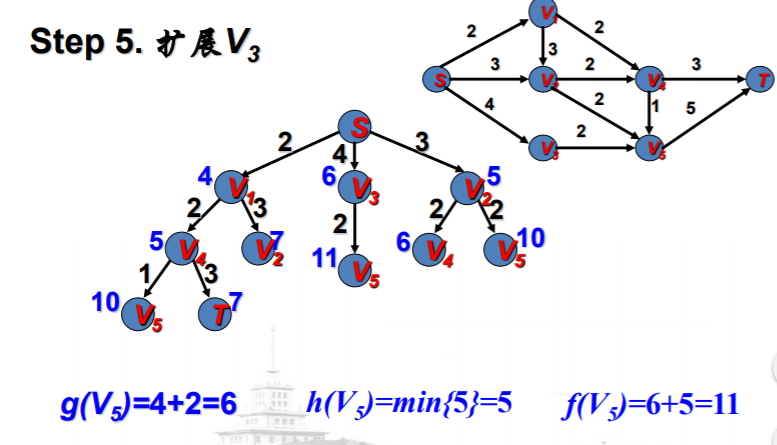

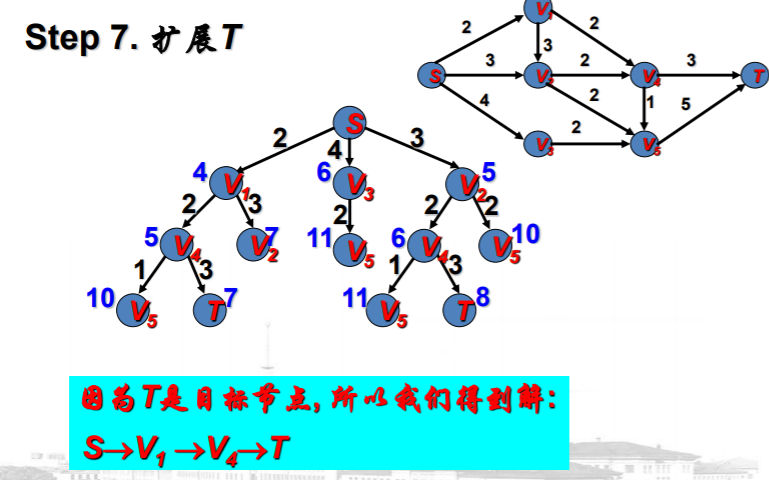
A*算法的有关知识--例子:最短路径问题的更多相关文章
- 机器学习算法的基本知识(使用Python和R代码)
本篇文章是原文的译文,然后自己对其中做了一些修改和添加内容(随机森林和降维算法).文章简洁地介绍了机器学习的主要算法和一些伪代码,对于初学者有很大帮助,是一篇不错的总结文章,后期可以通过文中提到的算法 ...
- (二)区块链的共识算法:PoS 及其 例子 代码 实现
作者:林冠宏 / 指尖下的幽灵 掘金:https://juejin.im/user/587f0dfe128fe100570ce2d8 博客:http://www.cnblogs.com/linguan ...
- Flyod 算法(两两之间的最短路径)
Flyod 算法(两两之间的最短路径)动态规划方法,通过相邻矩阵, 然后把最后的结果存在这么一个矩阵里面,(i,j), #include <iostream> #include <v ...
- 一个基于RSA算法的Java数字签名例子
原文地址:一个基于RSA算法的Java数字签名例子 一.前言: 网络数据安全包括数据的本身的安全性.数据的完整性(防止篡改).数据来源的不可否认性等要素.对数据采用加密算法加密可以保证数据本身的安全性 ...
- Eclipse直接运行算法第4版例子(重定向和读取指定路径文件)
Eclipse直接运行算法第4版例子(重定向和读取指定路径文件) 版权声明:本文为博主原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接和本声明. 本文链接:https://b ...
- C#算法设计之知识储备
前言 该文章的最新版本已迁移至个人博客[比特飞],单击链接 https://www.byteflying.com/archives/669 访问. 算法的讨论具有一定的规则,其中也包含一些不成文的约定 ...
- 浅析nodeJS中的Crypto模块,包括hash算法,HMAC算法,加密算法知识,SSL协议
node.js的crypto在0.8版本,这个模块的主要功能是加密解密. node利用 OpenSSL库(https://www.openssl.org/source/)来实现它的加密技术, 这是因为 ...
- 【视频编解码·学习笔记】7. 熵编码算法:基础知识 & 哈夫曼编码
一.熵编码概念: 熵越大越混乱 信息学中的熵: 用于度量消息的平均信息量,和信息的不确定性 越是随机的.前后不相关的信息,其熵越高 信源编码定理: 说明了香农熵越信源符号概率之间的关系 信息的熵为信源 ...
- 经典贪心算法(哈夫曼算法,Dijstra单源最短路径算法,最小费用最大流)
哈夫曼编码与哈夫曼算法 哈弗曼编码的目的是,如何用更短的bit来编码数据. 通过变长编码压缩编码长度.我们知道普通的编码都是定长的,比如常用的ASCII编码,每个字符都是8个bit.但在很多情况下,数 ...
随机推荐
- zabbbixs数据库常用操作
设置MariaDB数据库远程 GRANT ALL PRIVILEGES ON *.* TO 'root'@'%'IDENTIFIED BY 'admin' WITH GRANT OPTION; SEL ...
- spring:bean的生命周期
1.spring中bean的生命周期 (1)概念 在spring框架中,所有的bean对象都有生命周期,就是指bean的创建.初始化.服务.销毁的一个过程. (2)bean的生命周期 bean的定义 ...
- react 中发布订阅模式使用
react 中发布订阅模式使用 场景 怎么能将设计模式应用到我们的 React 项目中?以前一直在思考这个问题. 场景一 模块 A 模块 B 需要用到同一个数据 data,A 和 B 都会修改这份数据 ...
- Spring Boot 系统启动任务定义
前言 系统任务:在项目启动阶段要做一些数据初始化操作,这些操作有一个共同的特点,只在项目启动时进行,以后都不再执行. 应用场景:例如配置文件加载,数据库初始化等操作 Spring Boot出现之前 解 ...
- P5035金坷垃题解(快速幂的讲解)
首先经过读题,我们发现找到合格的金坷垃,怎么样的金坷垃才是合格的呢?(我们不难发现1肯定是合格的[题目已经给出了]) 然后我们开始手推一下之后合格的金坷垃: 2-1=1(合格) 3-1-1=1(不 ...
- Java知识系统回顾整理01基础06数组05复制数组
数组的长度是不可变的,一旦分配好空间,是多长,就多长,不能增加也不能减少 一.复制数组 把一个数组的值,复制到另一个数组中 System.arraycopy(src, srcPos, dest, de ...
- JavaScript 将十进制数转换成格式类似于 0x000100 或 #000100 的十六进制数
将十进制数转换成格式类似于 0x000100 或 #000100 的十六进制数 1 <!DOCTYPE html> 2 <html> 3 <head> 4 < ...
- 【学习笔记】Polya定理
笔者经多番周折终于看懂了\(\text{Burnside}\)定理和\(\text{Polya}\)定理,特来写一篇学习笔记来记录一下. 群定义 定义:群\((G,·)\)是一个集合与一个运算·所定义 ...
- 安装haproxy
安装依赖 yum install -y gcc pcre pcre-devel openssl openssl-devel 创建依赖账号,并禁止账号登录 useradd -M -s /sbin/nol ...
- xshell选项卡不见了
最近使用xshell的时候发现建立多个选项卡的时候,因为没有选项卡,所以不能切换. 弄了好一会儿才弄出来 点击会话选项卡或者Ctrl + Shift + T可以调出来
