P4821 [中山市选]生成树

题目链接

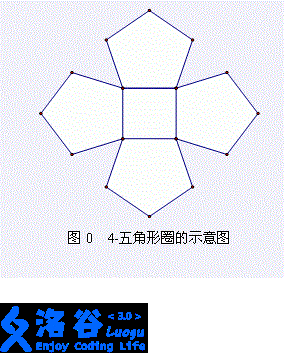
我们可以看一下题目中给的这张图。

首先，树是没有环的，所以我们要把所有的环上的边都删去一条。

我们可以现在每个五边形上删去一条边。

但删完之后我们会发现，里面还有一圈。

这时候，我们就要在这里面随便选一条边删去。

也就是，我们需要把n-1个五边形删去一条边，再把剩下的一个删掉两条边

那么方案数就是\(4 \times n \times 5 ^ {n-1}\)

补充：

可能有人会问，这难道不会多算吗？

我们再仔细分析一下。

为什么是\(4 \times n\) 而不是\(5 \times n\)

这个可以这么理解，删两条边的时候，我们强制删去里面的环的一条边，在删去一个五边形上的边就不会重了。

代码

#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
#define LL long long
int n,t;
const int p = 2007;
LL ksm(LL a,LL b)
{
	LL res = 1;
	for(; b; b >>= 1)
	{
		if(b & 1) res = res * a % p;
		a = a * a % p;
	}
	return res;
}
int main()
{
	scanf("%d",&t);
	while(t--)
	{
		scanf("%d",&n);
		printf("%lld\n",n* 4 *ksm(5,n-1) % p);
	}
	return 0;
}

听说，这题还可以用矩阵树过去，但蒟蒻我不会QAQ。

不知不觉又水了一道题。