DP斜率优化学习笔记

斜率优化

首先，可以进行斜率优化的DP方程式一般式为$dp[i]=\max_{j=1}^{i-1}/\min_{j=1}^{i-1}\{a(i)*x(j)+b(i)*y(j)\}$

其中$a(j)$和$b(j)$都是关于$j$的函数，在$O(1)$时间内可以计算得出

将方程式进行变形

$$dp[i]=a(i)*x(j)+b(i)*y(j)$$

$$dp[i]-a(i)*x(j)=b(i)*y(j)$$

$$y(j)=-\frac{a(i)}{b(i)}x(j)+\frac{dp[i]}{b(i)}$$

我们可以称$y=-\frac{a(i)}{b(i)}x+\frac{dp[i]}{b(i)}$为$i$的特征直线

那么对于$i$这个决策点来说，在$i$之前所有决策点$j$($j<i$)可以看作一个二维平面上的点，横坐标为$x(j)$，纵坐标为$y(j)$，那么i在寻找最优决策点的过程就是用i的特征直线去截平面上的每一个点，求出截距，找到最大/最小的$dp[i]$

但如果直接去做复杂度为$O(n^{2})$

那么可以通过维护在平面上维护凸包（根据具体的斜率正负和$b(i)$的正负决定维护上凸包还是下凸包），直线在平移过程中切到凸包的第一个点就是当前i的最优决策点，那么时间复杂度均摊$O(n)$

以$-\frac{a(i)}{b(i)}>0$，$b(i)>0$，$dp$取最小值为例

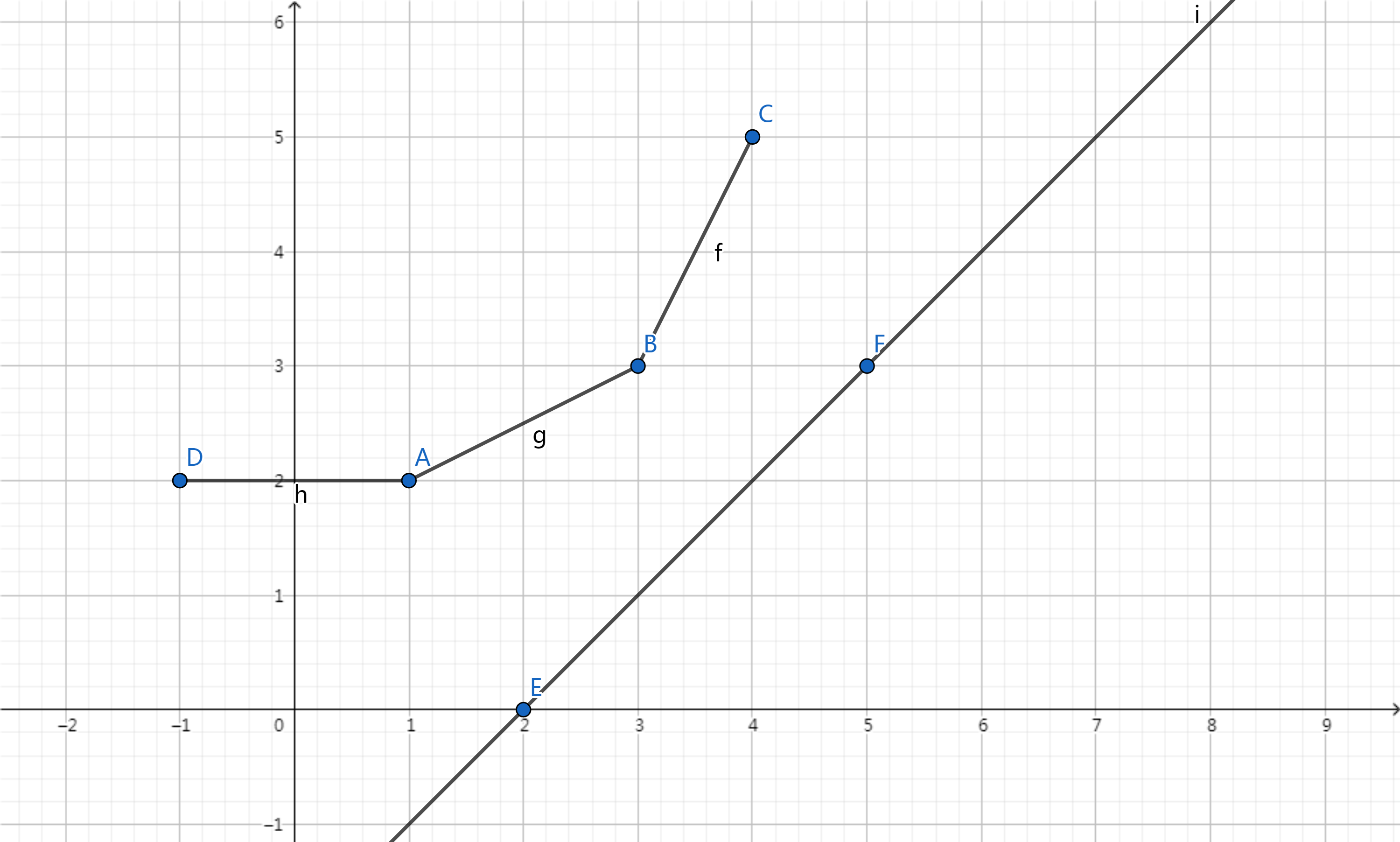
直线$EF$不断从截距无限小向上平移，直到截到凸包上的点

那么需要做的是维护凸包

1.若$x(i)$单调，斜率$-\frac{a(i)}{b(i)}$单调

所以在平面上的点是按顺序依次排列，去截的特征直线的斜率不断增加或减少

可以发现特征直线截到凸包上的第一个点记为$p$，那么$p$左边的点和$p$的直线的斜率$k_{1}$，$p$右边的点和$p$的直线的斜率$k_{2}$，特征直线的斜率一定介于$k_{1}$和$k_{2}$之间

那么可以利用单调队列来维护平面上的点的凸包，然后在单调队列队首不断维护当前特征直线的斜率，找到第一个大于或小于（根据凸包是上凸包还是下凸包决定）的决策点

时间复杂度$O(n)$

2.若$x(i)$单调，斜率不单调

仍然维护凸包，但此时特征直线的斜率没有规律，利用上面的结论可以二分凸包上两点的斜率，来找到第一个切到的点

时间复杂度$O(nlogn)$

3.若$x(i)$不单调，斜率不单调

对无规律的三个维度进行CDQ分治

具体见货币兑换的题解

#include <bits/stdc++.h>
#define min(a,b) (((a)<(b))?(a):(b))
#define max(a,b) (((a)>(b))?(a):(b))
#define eps 1e-9
using namespace std;
const int N=100100;
int n,h,t,q[N];
double s,dp[N];
struct node
{
    double a,b,r,k,x,y;
    int id;
}sh[N];
node p[N];
bool cmp(node a,node b)
{
    return a.k>b.k;
}
double slope(int i,int j)
{
    if (sh[j].x==sh[i].x) return 1e9;
    return (sh[j].y-sh[i].y)/(sh[j].x-sh[i].x);
}
void cdq(int l,int r)
{
    if (l==r)
    {
        dp[l]=max(dp[l],dp[l-1]);
        sh[l].x=sh[l].r*dp[l]/(sh[l].a*sh[l].r+sh[l].b);
        sh[l].y=dp[l]/(sh[l].a*sh[l].r+sh[l].b);
        return;
    }
    int mid=(l+r)>>1,tl=l-1,tr=mid;
    for (int i=l;i<=r;++i)
    {
        if (sh[i].id<=mid) p[++tl]=sh[i];
        else p[++tr]=sh[i];
    }
    for (int i=l;i<=r;i++) sh[i]=p[i];
    cdq(l,mid);
    h=0;t=-1;
    for (int i=l;i<=mid;++i)
    {
        while (h<t && slope(q[t],q[t-1])<slope(q[t],i)) t--;
        q[++t]=i;
    }
    for (int i=mid+1;i<=r;++i)
    {
        while (h<t && sh[i].k<slope(q[h],q[h+1])) h++;
        int j=q[h];
        dp[sh[i].id]=max(dp[sh[i].id],sh[i].a*sh[j].x+sh[i].b*sh[j].y);
    }
    cdq(mid+1,r);
    tl=l;tr=mid+1;
    int cnt=l-1;
    while (tl<=mid && tr<=r)
    {
        if (sh[tl].x-sh[tr].x<eps) p[++cnt]=sh[tl],tl++;
        else p[++cnt]=sh[tr],tr++;
    }
    for (int i=tl;i<=mid;++i) p[++cnt]=sh[i];
    for (int i=tr;i<=r;++i) p[++cnt]=sh[i];
    for (int i=l;i<=r;++i) sh[i]=p[i];
}
int main()
{
    scanf("%d%lf",&n,&s);
    for (int i=1;i<=n;i++)
    {
        scanf("%lf%lf%lf",&sh[i].a,&sh[i].b,&sh[i].r);
        sh[i].k=-sh[i].a/sh[i].b;sh[i].id=i;
    }
    sort(sh+1,sh+1+n,cmp);
    dp[0]=s;
    cdq(1,n);
    printf("%.3lf\n",dp[n]);
}

时间复杂度$O(nlogn)$

若在将序列上的问题转化到树上则利用点分治见购票

#include <bits/stdc++.h>
#define inf 1e18
#define int long long
#define re register
using namespace std;
const int N=2*1e5+100;
int n,T,sum[N],dp[N];
int h,t,q[N],sz[N],root,vi[N];
int tot,first[N],nxt[N*2],point[N*2];
int son[N],w;
struct node
{
    int fa,s,p,q,l;
}sh[N];
void add_edge(int x,int y)
{
    tot++;
    nxt[tot]=first[x];
    first[x]=tot;
    point[tot]=y;
}
bool cmp(int a,int b)
{
    return sum[a]-sh[a].l>sum[b]-sh[b].l;
}
double slope(int i,int j)
{
    return 1.0*(dp[j]-dp[i])/(1.0*(sum[j]-sum[i]));
}
int find(int l,int r,double k)
{
    if (r<l) return q[h];
    if (slope(q[l],q[l+1])>=k) return q[l];
    while (l<r)
    {
        int mid=l+((r-l+1)>>1);
        if (slope(q[mid],q[mid+1])<k) l=mid;
        else r=mid-1;
    }
    return q[l+1];
}
void dfs(int x)
{
    sz[x]=1;
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==sh[x].fa) continue;
        sum[u]=sum[x]+sh[u].s;
        dfs(u);
        sz[x]+=sz[u];
    }
}
void dfs_sz(int x,int fa)
{
    sz[x]=1;
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==fa || vi[u]) continue;
        dfs_sz(u,x);
        sz[x]+=sz[u];
    }
}
void dfs_rt(int x,int fa,int tot)
{
    bool bl=1;
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==fa || vi[u]) continue;
        dfs_rt(u,x,tot);
        if (sz[u]>tot/2) bl=0;
    }
    if (tot-sz[x]>tot/2) bl=0;
    if (bl) root=x;
}
void dfs_insert(int x,int fa)
{
    son[++w]=x;
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==fa || vi[u]) continue;
        dfs_insert(u,x);
    }
}
void divide(int x)
{
    vi[x]=1;
    vector <int> father;
    father.push_back(x);
    if (sh[x].fa && !vi[sh[x].fa])
    {
        for (int i=sh[x].fa;i!=0 && !vi[i];i=sh[i].fa)
          father.push_back(i);
        dfs_sz(sh[x].fa,x);
        dfs_rt(sh[x].fa,x,sz[sh[x].fa]);
        divide(root);
        for (re int i=1;i<(int)father.size();++i)
          if (sum[father[i]]>=sum[x]-sh[x].l)
            dp[x]=min(dp[x],dp[father[i]]+(sum[x]-sum[father[i]])*sh[x].p+sh[x].q);
    }
    w=0;
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==sh[x].fa || vi[u]) continue;
        dfs_insert(u,x);
    }
    sort(son+1,son+1+w,cmp);
    h=n+1;t=n;
    for (re int i=1,j=0;i<=w;++i)
    {
        int u=son[i];
        while (j<(int)father.size() && sum[father[j]]>=sum[u]-sh[u].l)
        {
            while (h<t && slope(q[h],q[h+1])<slope(q[h],father[j])) h++;
            q[--h]=father[j];
            j++;
        }
        if (h>t) continue;
        int pos=find(h,t-1,1.0*sh[u].p);
        dp[u]=min(dp[u],dp[pos]+(sum[u]-sum[pos])*sh[u].p+sh[u].q);
    }
    for (re int i=first[x];i!=-1;i=nxt[i])
    {
        int u=point[i];
        if (u==sh[x].fa || vi[u]) continue;
        dfs_sz(u,x);
        dfs_rt(u,x,sz[u]);
        divide(root);
    }
}
signed main()
{
    tot=-1;
    memset(first,-1,sizeof(first));
    memset(nxt,-1,sizeof(nxt));
    scanf("%lld%lld",&n,&T);
    for (re int i=2;i<=n;++i)
    {
        scanf("%lld%lld%lld%lld%lld",&sh[i].fa,&sh[i].s,&sh[i].p,&sh[i].q,&sh[i].l);
        add_edge(sh[i].fa,i);
        add_edge(i,sh[i].fa);
    }
    sh[1].fa=0;dp[1]=0;
    for (re int i=2;i<=n;++i) dp[i]=inf;
    dfs(1);
    dfs_rt(1,0,sz[1]);
    divide(root);
    for (re int i=2;i<=n;++i) printf("%lld\n",dp[i]);
}