2020-06-22：已知两个非负数的异或值为M，两数之和为N，求这两个数？

福哥答案2020-06-22：

1.遍历法
时间复杂度：O(N)
最好空间复杂度：O(1)
平均空间复杂度：O(sqrt(N))
最坏空间复杂度：O(N)
[0,N/2]依次遍历，符合条件的就是需要的结果。

2.位运算法
最好时间复杂度：O(1)
平均时间复杂度：O(sqrt(N))
最坏时间复杂度：O(N)
最好空间复杂度：O(1)
平均空间复杂度：O(sqrt(N))
最坏空间复杂度：O(N)

1100100 两数和N=100，已知
0010100 异或值M=20，已知
1010000 差N-M=80，如果差为负数或者差为奇数，直接返回空
0101000 差右移1位。

0010100 异或值M=20，已知
0101000 差右移1位。
将上面两个二进制数换成中文如下：
同同异同异同同
零幺零幺零零零

---

零幺异幺异零零=01x1x00，x代表0和1，只要满足这样的数就行。规则：同零=0，同幺=1，异零=x，异幺=不符合条件。只要出现了异幺，直接返回空。

golang代码如下：

package test23_xorandsum

import (
    "fmt"
    "testing"
)

const (
    SameOne = 1
    SameZero = 0
    Different = 2
    DifferentZero = 0
)

//go test -v -test.run TestXorAndSum
func TestXorAndSum(t *testing.T) {
    //M := uint(20)
    //N := uint(100)

    M := uint(1)
    N := uint(9)
    fmt.Println("M = ", M)
    fmt.Println("N = ", N)
    fmt.Println("遍历法：", xorAndSum1(M, N))
    fmt.Println("位操作法：", xorAndSum2(M, N))
}

//M是两个数异或值
//N是两个数之和
//1.遍历法
func xorAndSum1(M uint, N uint) [][]uint {
    ret := make([][]uint, 0) //返回多个值
    n := N >> 1 //只需要遍历一半

    temp := uint(0)
    for i := uint(0); i <= n; i++ {
        temp = M ^ i
        if N-i == temp { //找到异或值和两数和的两个数了
           ret = append(ret, []uint{i, temp})
        }
    }

    return ret
}

//M是两个数异或值
//N是两个数之和
//2.位操作法
func xorAndSum2(M uint, N uint) [][]uint {
    ret := make([][]uint, 0) //返回多个值

    //两数之和小于两数异或值，不存在这样的情况
    if N < M {
    return ret
    }

    sub := N - M //差值

    //不能被2整除，不存在这样的情况
    if sub&1 == 1 {
        return ret
    }

    //生成中间结果
    sub >>= 1 //差值右移动一位，方便做判断
    slicebit := make([]byte, 0)
    kind := uint(1)
    for sub > 0 || M > 0 {
        if M&1 == 1 { //当前位，两数不同
            if sub&1 == 1 { //不存在这样的情况
                return ret
           } else {
                slicebit = append(slicebit, Different)
                kind <<= 1
            }
        } else { //当前位，两数相同
            if sub&1 == 1 { //当前位肯定都为1
                slicebit = append(slicebit, SameOne)
            } else { //当前位肯定都为0
                slicebit = append(slicebit, SameZero)
            }
        }

        sub >>= 1
        M >>= 1
    }

    //两数异或值M第1个1位0，作用是去重
    for i := len(slicebit) - 1; i >= 0; i-- {
        if slicebit[i] == Different {
            slicebit[i] = DifferentZero
            kind >>= 1
            break
        }
    }

    //生成结果
    retsingle := uint(0)
    tempi1 := uint(0)
    tempi2 := uint(0)
    for i := uint(0); i < kind; i++ { //遍历种类
        retsingle = 0
        tempi1 = i

        //这段代码可以省略，影响打印顺序
        //00=0 01=1 10=2 11=3
        //00=0 10=2 01=1 11=3
        kindtemp := kind
        tempi2 = 0
        for {
            tempi2 <<= 1
            tempi2 |= tempi1 & 1
            tempi1 >>= 1

            kindtemp >>= 1
            if kindtemp <= 1 {
                break
        }
    }
    tempi1 = tempi2

    //生成结果
    for j := len(slicebit) - 1; j >= 0; j-- {
        retsingle <<= 1
        if slicebit[j] <= SameOne {
            retsingle |= uint(slicebit[j])
        } else {
                retsingle |= uint(tempi1 & 1)
                tempi1 >>= 1
            }
        }

        //将结果保存起来
        ret = append(ret, []uint{retsingle, N - retsingle})
    }

    return ret
}

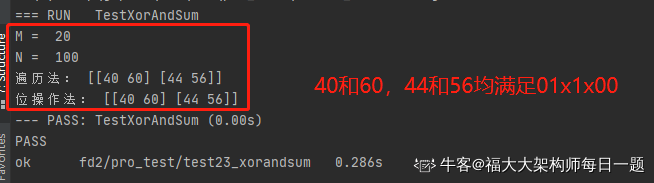
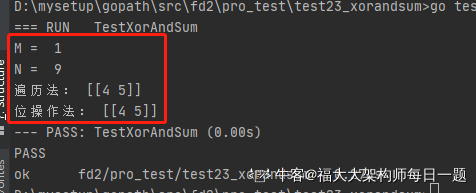
　　敲命令go test -v -test.run TestXorAndSum，执行结果如下：