《MySQL数据库》MySQL备份恢复

前言

MySQL数据库最重要的部分就是数据，所以保证数据不被损坏尤为重要，大家都知道911事件，当时非常多的数据丢失，导致经济混乱。接下来我们就来讲讲MySQL是如何保障数据完整，应对特殊情况，如何恢复等。

备份

备份检查：保证备份没有问题，并且定期演练恢复数据。

备份方式：逻辑备份，物理备份。

逻辑备份方式：mysqldump(MDP),replication,mydumper,load data in file。

物理备份方式：MySQL Enterprise Backup(企业版) ， percona Xtrabackup (PBK,XBP)

1. mysqldump(MDP)

InnoDB 可以使用快照备份，通过建库，建表，插入语句备份数据。

非Innodb 表备份需要锁表， 非Innodb 表主要是MySQL系统表。

参数说明：

mysqldump  需要连接到数据库，连接方式和mysql 一致。

创建备份目录

mkdir -p backup    -- linux 下执行创建文件夹
chown -R mysql.mysql /usr/local/mysql/backup   -- linux 下执行赋权

备份命令：

mysqldump -uroot -proot -A > /usr/local/mysql/backup/mysqlbackup.sql  -- -A 备份全库的意思

备份多库

mysqldump -u cop -p -B cop copdb   > copdb1.sql       -- -B参数导出多个库。

备份某些表

mysqldump -uroot -proot castledata test test1 > /usr/local/mysql/backup/mysqlbackup1.sql -- 导出一张表的结构和数据：castledata 库名；cop_toperator,cop_tsys是表名。

其实这个时候你会发现一个问题，库备份了，但是数据还是会继续操作的，真的出现误删除数据库，如何才能完整的恢复呢。

第一反应就是 备份加binlog ,但是binlog的开始位置点却不好找， 如何才能准确无误的找到这个开始位置点呢？

重点：

--master-data=2    -- 2：表示会再备份文件中加入一句注释，写下binlog文件和开始位置点。 默认是0。

mysqldump -uroot -proot --master-data=2  castledata test test1 > /usr/local/mysql/backup/mysqlbackup2.sql     -- 使用上面的参数备份

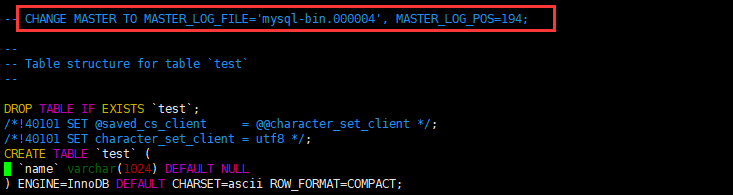
mysqldump -uroot -proot -F -B castledata > /usr/local/mysql/backup/mysqlbackup3.sql    

-F 参数是备份的时候切一个新的binlog日志。

--single-transaction           开启事务，获取快照，对innodb存储引擎有效。

-R                                      备份存储过程及函数

--triggers                            备份触发器

-E                                       备份事件

--max_allowed_packet       客户发数据包到服务端的大小，备份的是表示服务端发到客户端的大小

完整生产备份语句：

mysqldump -uroot -proot -R --triggers -E --single-transaction --master-data=2 --max_allowed_packet=64 -B castledata > /usr/local/mysql/backup/mysqlbackup5.sql

恢复

模拟备份到恢复的过程：

第一步准备原始数据：

create database backup;
use backup
create table t1 (id int);
insert into t1 values(1),(2),(3);
insert into t1 values(11),(22),(33);
insert into t1 values(111),(222),(333);
insert into t1 values(1111),(2222),(3333);
insert into t1 values(11111),(22222),(33333);
commit;

第二步备份数据：

mysqldump -uroot -proot -R --triggers -E --single-transaction --master-data=2 --max_allowed_packet=64 -B backup > /usr/local/mysql/backup/mysqlbackup_`date +%F `.sql

第三步模拟后续数据操作：

create table t2 (id int);
insert into t2 values(1),(2),(3);
insert into t2 values(11),(22),(33);
insert into t2 values(111),(222),(333);
insert into t2 values(1111),(2222),(3333);
insert into t2 values(11111),(22222),(33333);
commit;

第四步逻辑操作出错：

drop database backup;

第五步恢复数据：

1. 获取最近一次备份文件中的binlog 起点信息：

binlog 日志原理：https://www.cnblogs.com/jssj/p/13472394.html

2.恢复备份数据

set sql_log_bin = 0;
source /usr/local/mysql/backup/mysqlbackup_2020-08-18.sql;
set sql_log_bin = 1;

3. 截取binlog

起点：在第一步中已经获取， 终点：使用命令 " show binlog events in 'mysql-bin.000005' ; "  查询

取 3362 即可。  执行一下命令截取

mysqlbinlog --start-position=1861 --stop-position=3362 /usr/local/mysql/binlog/mysql-bin.000005 > /usr/local/mysql/backup_binlog.sql

4. 恢复binlog 日志

set sql_log_bin = 0;
source /usr/local/mysql/backup_binlog.sql;
set sql_log_bin = 1;

ok 恢复失败。binlog的恢复。原因为我们开启了GTID 所以截取命令需要加入 参数  --skip-gtids   。 不校验GTID号。

重新截取binlog：

mysqlbinlog --skip-gtids --start-position=1861 --stop-position=3362 /usr/local/mysql/binlog/mysql-bin.000005 > /usr/local/mysql/backup_binlog.sql

set sql_log_bin = 0;
source /usr/local/mysql/backup_binlog.sql;
set sql_log_bin = 1;

ok 恢复成功。验证数据。

额外扩展：从全备中获取单库，创建表，插入数据

1、获得表结构
# sed -e'/./{H;$!d;}' -e 'x;/CREATE TABLE `city`/!d;q'  full.sql>createtable.sql
2、获得INSERT INTO 语句，用于数据的恢复
# grep -i 'INSERT INTO `city`'  full.sqll >data.sql &
3.获取单库的备份
# sed -n '/^-- Current Database: `world`/,/^-- Current Database: `/p' all.sql >world.sql

总结

上面讲的都是逻辑备份，MySQL还可以支持物理备份，可以使用工具Percona-XtraBackup 来实现。