滑动窗口（Sliding Window）技巧总结

什么是滑动窗口（Sliding Window）

The Sliding Problem contains a sliding window which is a sub – list that runs over a Large Array which is an underlying collection of elements.

滑动窗口算法可以用以解决数组/字符串的子元素问题，它可以将嵌套的循环问题，转换为单循环问题，降低时间复杂度。

比如找最长的全为1的子数组长度。滑动窗口一般从第一个元素开始，一直往右边一个一个元素挪动。当然了，根据题目要求，我们可能有固定窗口大小的情况，也有窗口的大小变化的情况。

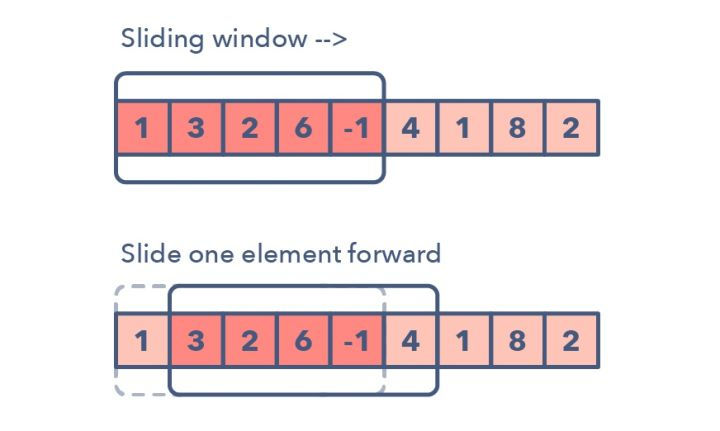
如何判断使用滑动窗口算法

如果题目中求的结果有以下情况时可使用滑动窗口算法：

• 最小值 Minimum value
• 最大值 Maximum value
• 最长值 Longest value
• 最短值 Shortest value
• K值 K-sized value

算法模板与思路

/* 滑动窗口算法框架 */
void slidingWindow(string s, string t) {
    unordered_map<char, int> need, window;
    for (char c : t) need[c]++;

    int left = 0, right = 0;
    int valid = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        // 右移窗口
        right++;
        // 进行窗口内数据的一系列更新
        ...

        /*** debug 输出的位置 ***/
        printf("window: [%d, %d)\n", left, right);
        /********************/

        // 判断左侧窗口是否要收缩
        while (window needs shrink) {
            // d 是将移出窗口的字符
            char d = s[left];
            // 左移窗口
            left++;
            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

滑动窗口算法的思路：

1. 在字符串 S 中使用双指针中的左右指针技巧，初始化 left = right = 0 ，把索引左闭右开区间 [left, right) 称为一个「窗口」。
2. 不断地增加 right 指针扩大窗口 [left, right) ，直到窗口中的字符串符合要求（包含了 T 中的所有字符）。
3. 此时停止增加 right ，转而不断增加 left 指针缩小窗口 [left, right) ，直到窗口中的字符串不再符合要求（不包含 T 中的所有字符了）。同时，每次增加 left ，都要更新一轮结果。
4. 重复第2和第3步，直到 right 到达字符串 S 的尽头。

needs 和 window 相当于计数器，分别记录 T 中字符出现次数和「窗口」中的相应字符的出现次数。

开始套模板之前，要思考以下四个问题：

1. 当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？
2. 什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？
3. 当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？
4. 我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

滑动窗口问题实例

最小覆盖子串

LeetCode题目：76.最小覆盖子串

1、阅读且分析题目

题目中包含关键字：时间复杂度O(n)、字符串、最小子串。可使用滑动窗口算法解决。

2. 思考滑动窗口算法四个问题

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

更新 window 中加入字符的个数，判断 need 与 window 中的字符个数是否相等，相等则 valid++ 。

2、什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？

当 window 包含 need 中的字符及个数时，即 valid == len(need) 。

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

更新 window 中移出字符的个数，且判断 need 与 window 中的移出字符个数是否相等，相等则 valid-- 。

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

在缩小窗口时，因为求的是最小子串。

3. 代码实现

func minWindow(s string, t string) string {
	need, window := make(map[byte]int), make(map[byte]int)
	for i := 0; i < len(t); i++ { // 初始化 need
		if _, ok := need[t[i]]; ok {
			need[t[i]]++
		} else {
			need[t[i]] = 1
		}
	}

	left, right, valid := 0, 0, 0
	start, slen := 0, len(s)+1 // 设置长度为 len(s) + 1 表示此时没有符合条件的子串
	for right < len(s) { // 滑动窗口向右扩大
		c := s[right]
		right++

		if _, ok := need[c]; ok { // 向右扩大时，更新数据
			if _, ok := window[c]; ok {
				window[c]++
			} else {
				window[c] = 1
			}

			if window[c] == need[c] {
				valid++
			}
		}

		for valid == len(need) { // 当窗口包括 need 中所有字符及个数时，缩小窗口

			if right-left < slen {  // 缩小前，判断是否最小子串
				start = left
				slen = right - left
			}

			d := s[left]
			left++

			if v, ok := need[d]; ok { // 向左缩小时，更新数据
				if window[d] == v {
					valid--
				}
				window[d]--
			}
		}
	}

	if slen == len(s)+1 { // 长度 len(s) + 1 表示此时没有符合条件的子串
		return ""
	} else {
		return s[start : start+slen]
	}
}

4. 复杂度分析

• 时间复杂度：O(n)，n 表示字符串 s 的长度。遍历一次字符串。
• 空间复杂度：O(m)，m 表示字符串 t 的长度。使用了两个哈希表，保存字符串 t 中的字符个数。

字符串排列

LeetCode题目：567.字符串的排列

1、阅读且分析题目

题目中包含关键字：字符串、子串，且求 s2 中是否包含 s1 的排列，即求是否包含长度 k 的子串。可使用滑动窗口算法解决。

2. 思考滑动窗口算法四个问题

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

更新 window 中加入字符的个数，判断 need 与 window 中的字符个数是否相等，相等则 valid++ 。

2、什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？

当 window 包含 need 中的字符及个数时，即 valid == len(need) 。

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

更新 window 中移出字符的个数，且判断 need 与 window 中的移出字符个数是否相等，相等则 valid-- 。

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

无论在扩大时或缩小窗口时都可以，因为求的是固定长度的子串。选择在缩小窗口时更新。

3. 代码实现

func checkInclusion(s1 string, s2 string) bool {
	if s1 == s2 {
		return true
	}

	need, window := make(map[byte]int), make(map[byte]int)

	for i := 0; i < len(s1); i++ {
		if _, ok := need[s1[i]]; ok {
			need[s1[i]]++
		} else {
			need[s1[i]] = 1
		}
	}

	left, right := 0, 0
	valid := 0

	for right < len(s2) {
		c := s2[right]
		right++

		if _, ok := need[c]; ok {
			if _, ok := window[c]; ok {
				window[c]++
			} else {
				window[c] = 1
			}
			if window[c] == need[c] {
				valid++
			}
		}

		for valid == len(need) {

			if right-left == len(s1) {
				return true
			}

			d := s2[left]
			left++

			if _, ok := need[d]; ok {
				if _, ok := window[d]; ok {
					if window[d] == need[d] {
						valid--
					}
					window[d]--
				}
			}
		}
	}

	return false
}

4. 复杂度分析

• 时间复杂度：O(n)，n 表示字符串 s2 的长度。遍历一次字符串。
• 空间复杂度：O(m)，m 表示字符串 s1 的长度。使用了两个哈希表，保存字符串 s1 中的字符个数。

找所有字母异位词

LeetCode题目：438.找到字符串中所有字母异位词

1、阅读且分析题目

题目中包含关键字：字符串，且求 s 中的所有 p 的字母异位词的子串。可使用滑动窗口算法解决。

2. 思考滑动窗口算法四个问题

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

更新 window 中加入字符的个数，判断 need 与 window 中的字符个数是否相等，相等则 valid++ 。

2、什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？

当 window 包含 need 中的字符及个数时，即 valid == len(need) 。

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

更新 window 中移出字符的个数，且判断 need 与 window 中的移出字符个数是否相等，相等则 valid-- 。

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

无论在扩大时或缩小窗口时都可以，因为求的是固定长度的子串。选择在缩小窗口时更新。

3. 代码实现

func findAnagrams(s string, p string) []int {
	need, window := make(map[byte]int), make(map[byte]int)
	for i := 0; i < len(p); i++ { // 初始化
		if _, ok := need[p[i]]; ok {
			need[p[i]]++
		} else {
			need[p[i]] = 1
		}
	}

	left, right := 0, 0
	valid := 0

	ans := make([]int, 0)

	for right < len(s) {
		c := s[right]
		right++

		if _, ok := need[c]; ok {
			if _, ok := window[c]; ok {
				window[c]++
			} else {
				window[c] = 1
			}
			if need[c] == window[c] {
				valid++
			}
		}

		for valid == len(need) {
			if right-left == len(p) {
				ans = append(ans, left)
			}

			d := s[left]
			left++

			if _, ok := need[d]; ok {
				if _, ok := window[d]; ok {
					if need[d] == window[d] {
						valid--
					}
					window[d]--
				}
			}
		}
	}

	return ans
}

4. 复杂度分析

• 时间复杂度：O(n)，n 表示字符串 s 的长度。遍历一次字符串。
• 空间复杂度：O(m)，m 表示字符串 p 的长度。使用了两个哈希表，保存字符串 p 中的字符个数。

最长无重复子串

LeetCode题目：3. 无重复字符的最长子串

1、阅读且分析题目

题目中包含关键字：时间复杂度O(n)、字符串、最小子串。可使用滑动窗口算法解决。

2. 思考滑动窗口算法四个问题

1、当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？

更新 window 中加入字符的个数，及当 window 中的某个字符个数 == 2时，更新 valid == false 。

2、什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？

当 window 中的字符及个数 == 2时，即 valid == false 。

3、当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？

更新 window 中移出字符的个数，且判断 window 中移出字符个数是否 == 2 ，相等则 valid == true 。

4、我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

在扩大窗口时，因为求的是最大子串。

3. 代码实现

func lengthOfLongestSubstring(s string) int {
	if s == "" { // 当字符串为空时，返回0
		return 0
	}

	window := make(map[byte]int)

	left, right, max := 0, 0, 0
	valid := true

	for right < len(s) {
		c := s[right]
		right++

		if _, ok := window[c]; !ok { // 初始化
			window[c] = 0
		}
		window[c]++         // 累加
		if window[c] == 2 { // 当出现重复字符时
			valid = false
		} else { // 否则累加不重复子串长度，并且判断是否当前最长
			if max < right-left {
				max = right - left
			}
		}

		for valid == false {
			d := s[left]
			left++

			if window[d] == 2 {
				valid = true
			}
			window[d]--
		}
	}
	return max
}

4. 复杂度分析

• 时间复杂度：O(n)，n 表示字符串 s 的长度。遍历一次字符串。
• 空间复杂度：O(n)，n 表示字符串 s 的长度。使用了哈希表，保存不重复的字符个数。

总结

• 滑动窗口算法可以用以解决数组/字符串的子元素问题，它可以将嵌套的循环问题，转换为单循环问题，降低时间复杂度。
• 问题中包含字符串子元素、最大值、最小值、最长、最短、K值等关键字时，可使用滑动窗口算法。
• 模板中的向左和向右时的处理是对称的。
• 套模板前思考四个问题：
  1. 当移动 right 扩大窗口，即加入字符时，应该更新哪些数据？
  2. 什么条件下，窗口应该暂停扩大，开始移动_left_ 缩小窗口？
  3. 当移动 left 缩小窗口，即移出字符时，应该更新哪些数据？
  4. 我们要的结果应该在扩大窗口时还是缩小窗口时进行更新？

参考资料

• Sliding Window Algorithm C Program
• 我写了一首诗，把滑动窗口算法变成了默写题