HDU6532 Chessboard (最大费用流)

题意:棋盘上有n个棋子 每个棋子都有收益

　　 现在给定1e5条线 有横着的 竖着的

　　 规定只能在线的一侧选最多ki个棋子

　　 问最大收益

题解:写自闭的一道题 很容易想到是网络流 但是建图有点难

　　 第一道最大费用流 居然是边权取反 跑最小费用最大流!

　　 先离散化坐标 然后可以用点代替一条横线 一条竖线

　　 如果x，y有一个棋子 就将x所在的横线 向y所在的竖线连一个权值为1 收益为花费的边

　　 这里要跑最大收益 所以收益要取反

　　 同时从小到大的每相邻两个横线之间连一条收益为0 边权为x较小的点所受限制条件

　　 竖线之间也连一条收益为0 边权为y较大的点所受限制条件

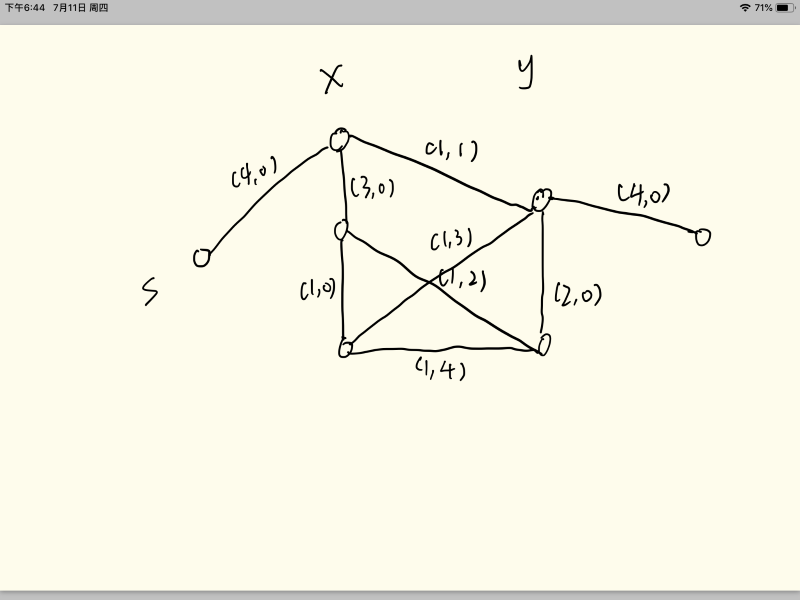
　　 好像越扯越复杂了...  总之就是直接上图吧

　　 左边表示x = 1， x = 2, x = 3三条线 右边表示y = 1, y = 2 两条线

　　

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int INF = 0x3f3f3f3f;
int n, m, s, t, cnt, maxflow;
ll mincost;
int cntx, cnty;
int xid[505];
int yid[505];
int kx[505];
int ky[505];

struct po {
    int x, y, id;
    int tx, ty;
}q[505];

bool cmp1(po A, po B) {return A.x < B.x;}
bool cmp2(po A, po B) {return A.y < B.y;}
bool cmp3(po A, po B) {return A.id < B.id;}

int findx(int x) {
    if(x <= xid[1]) return 1;
    if(x > xid[cntx]) return -1;
    int l = 2, r = cntx;
    int mid = l + r >> 1;
    while(l + 1 < r) {
        mid = l + r >> 1;
        if(x >= xid[mid]) l = mid;
        else r = mid;
    }
    if(x <= xid[l]) return l;
    else return r;
}

int findy(int y) {
    if(y <= yid[1]) return 1;
    if(y > yid[cnty]) return -1;
    int l = 2, r = cnty;
    int mid = l + r >> 1;
    while(l + 1 < r) {
        mid = l + r >> 1;
        if(y >= yid[mid]) l = mid;
        else r = mid;
    }
    if(y <= yid[l]) return l;
    else return r;
}

struct node {
    int to, nex, val, cost;
}E[100005];
int head[1005];
int cur[1005];

void addedge(int x, int y, int va, int cos) {
    E[++cnt].to = y; E[cnt].nex = head[x]; head[x] = cnt; E[cnt].val = va; E[cnt].cost = cos;
    E[++cnt].to = x; E[cnt].nex = head[y]; head[y] = cnt; E[cnt].val = 0; E[cnt].cost = -cos;
}

int inque[1005];
int dis[1005];
int vis[1005];
bool spfa() {
    for(int i = 1; i <= cntx + cnty + 2; i++) inque[i] = 0, dis[i] = INF, cur[i] = head[i];
    queue<int> que;
    que.push(s);
    dis[s] = 0, inque[s] = 1;

    while(!que.empty()) {
        int u = que.front();
        que.pop();
        inque[u] = 0;

        for(int i = head[u]; i; i = E[i].nex) {
            int v = E[i].to;
            if(E[i].val > 0 && dis[v] > dis[u] + E[i].cost) {
                dis[v] = dis[u] + E[i].cost;
                if(!inque[v]) {
                    inque[v] = 1;
                    que.push(v);
                }
            }
        }
    }
    return dis[t] != INF;
}

int dfs(int x, int flow) {
    if(x == t) {
        vis[t] = 1;
        maxflow += flow;
        return flow;
    }

    vis[x] = 1;
    int used = 0;
    int rflow = 0;
    for(int i = cur[x]; i; i = E[i].nex) {
        cur[x] = i;
        int v = E[i].to;
        if(E[i].val > 0 && (!vis[v] || v == t) && dis[v] == dis[x] + E[i].cost) {
            if(rflow = dfs(v, min(flow - used, E[i].val))) {
                used += rflow;
                E[i].val -= rflow;
                E[i ^ 1].val += rflow;
                mincost += 1LL * E[i].cost * rflow;
                if(used == flow) break;
            }
        }
    }
    return used;
}

void dinic() {
    maxflow = mincost = 0;
    while(spfa()) {
        vis[t] = 1;
        while(vis[t]) {
            memset(vis, 0, sizeof(vis));
            dfs(s, INF);
        }
    }
}

int main() {

    while(~scanf("%d", &n)) {
        cnt = 1;
        memset(kx, 0, sizeof(kx));
        memset(ky, 0, sizeof(ky));
        memset(head, 0, sizeof(head));
        cntx = cnty = 0;
        for(int i = 1; i <= n; i++) scanf("%d%d", &q[i].x, &q[i].y), q[i].id = i;
        q[0].x = q[0].y = 0;
        sort(q + 1, q + 1 + n, cmp1);
        for(int i = 1; i <= n; i++) {
            if(q[i].x != q[i - 1].x)
                xid[++cntx] = q[i].x;
            q[i].tx = cntx;
        }

        sort(q + 1, q + 1 + n, cmp2);
        for(int i = 1; i <= n; i++) {
            if(q[i].y != q[i - 1].y)
                yid[++cnty] = q[i].y;
            q[i].ty = cnty;
        }
        sort(q + 1, q + 1 + n, cmp3);

        scanf("%d", &m);
        for(int i = 1; i <= m; i++) {
            getchar();
            char a; int b, c;
            scanf("%c %d %d", &a, &b, &c);
            if(a == 'R') {
                int tmp = findx(b);
                if(tmp == -1) continue;
                if(kx[tmp] == 0) kx[tmp] = c;
                else kx[tmp] = min(kx[tmp], c);
            } else if(a == 'C') {
                int tmp = findy(b);
                if(tmp == -1) continue;
                if(ky[tmp] == 0) ky[tmp] = c;
                else ky[tmp] = min(ky[tmp], c);
            }
        }

        s = cntx + cnty + 1;
        t = s + 1;
        int lasx = n;
        for(int i = 1; i <= cntx; i++) {
            if(kx[i]) lasx = min(lasx, kx[i]);
            if(i == 1) addedge(s, i, lasx, 0);
            else addedge(i - 1, i, lasx, 0);
        }

        int lasy = n;
        for(int i = 1; i <= cnty; i++) {
            if(ky[i]) lasy = min(lasy, ky[i]);
            if(i == 1) addedge(cntx + i, t, lasy, 0);
            else addedge(cntx + i, cntx + i - 1, lasy, 0);
        }
        for(int i = 1; i <= n; i++) {
            addedge(q[i].tx, q[i].ty + cntx, 1, -q[i].id);
        }

        dinic();
        printf("%lld\n", -mincost);
    }
    return 0;
}