cf492E Vanya and Field

E. Vanya and Field

time limit per test 2 seconds

memory limit per test 256 megabytes

input standard input

output standard output

Vanya decided to walk in the field of size n × n cells. The field contains m apple trees, the i-th apple tree is at the cell with coordinates(xi, yi). Vanya moves towards vector (dx, dy). That means that if Vanya is now at the cell (x, y), then in a second he will be at cell 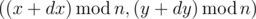. The following condition is satisfied for the vector: 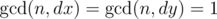, where  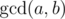is the largest integer that divides both a and b. Vanya ends his path when he reaches the square he has already visited.

Vanya wonders, from what square of the field he should start his path to see as many apple trees as possible.

Input

The first line contains integers n, m, dx, dy(1 ≤ n ≤ 106, 1 ≤ m ≤ 105, 1 ≤ dx, dy ≤ n) — the size of the field, the number of apple trees and the vector of Vanya's movement. Next m lines contain integers xi, yi (0 ≤ xi, yi ≤ n - 1) — the coordinates of apples. One cell may contain multiple apple trees.

Output

Print two space-separated numbers — the coordinates of the cell from which you should start your path. If there are several answers you are allowed to print any of them.

Sample test(s)

input

5 5 2 3
0 0
1 2
1 3
2 4
3 1

output

1 3

input

2 3 1 1
0 0
0 1
1 1

output

0 0

Note

In the first sample Vanya's path will look like: (1, 3) - (3, 1) - (0, 4) - (2, 2) - (4, 0) - (1, 3)

In the second sample: (0, 0) - (1, 1) - (0, 0)

这道真是想法题了……

首先，从一个点出发一直走，它能到达的点的集合一定是一个环（因为要是能一直走到当前没走过的点那还得了）

然后要考虑这样的集合有什么性质

把第一个样例拿来模拟一下，不取模看的更清楚：

(1,3)

(3,6)

(5,9)

(7,12)

(9,15)

(11,18)

这样规律就很清楚了吧：对于n*n的格子，从一个点出发走了n步之后回到这个点，集合里一定有n个元素

所以有n个集合，用(0,0)到(0,n-1)共n个在不同集合的点标记它们

然后从(0,0)开始枚举往上走，就可以算出每一行中哪一个格子是和(0,0)在同一集合

那么其他点依次右移一格就知道在那一个集合里了

最后每一个集合里的点都是可以相互到达的，随便输出一个就好了

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<queue>
#include<deque>
#include<set>
#include<map>
#include<ctime>
#define LL long long
#define inf 0x7ffffff
#define pa pair<int,int>
#define pi 3.1415926535897932384626433832795028841971
#define mod 1000007
using namespace std;
inline LL read()
{
    LL x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
struct po{
	int x,y,rnk;
}point[1000010];
int head[1000010];
int n,m,xx,yy,cnt,ans,mx;
int nx,ny;
int floor[1000010];
int sum[1000010];
int main()
{
	n=read();m=read();xx=read();yy=read();
	for(int i=1;i<=n+1;i++)
	{
		nx+=xx;ny+=yy;
		if (nx>=n)nx-=n;
		if (ny>=n)ny-=n;
		floor[nx]=ny;
	}
	for (int i=1;i<=m;i++)
	{
		int nx=read();
		int ny=read();
		int flo=floor[nx];
		int dire=ny-flo;if (dire<0)dire+=n;
		sum[dire]++;
		if(sum[dire]>mx)
		{
			mx=sum[dire];
			ans=dire;
		}

	}
	printf("%d %d\n",0,ans);
	return 0;
}