RVO算法

http://blog.sina.com.cn/s/blog_6ad33d350102xqal.html

简介

在介绍VO，RVO之前，需要先介绍路径规划。

对Agent进行路径规划，实际上要完成的任务就是让Agent从点A无碰撞地移动到点B。而路径规划的过程是层次化的，其基本框架大致如下：

• High level:
  dijkstra等算法。

• Low level:
  VO, RVO, ORCA等底层避障算法。

• High level:
  通过dijkstra算法，得到路径为: 教学楼→饭堂→体育馆→图书馆→宿舍楼。

• Low level:
  通过底层避障算法如VO，RVO，ORCA等底层避障算法，保证我们走的每一段路（e.g. 教学楼→饭堂），都不会跟别的同学发生碰撞。

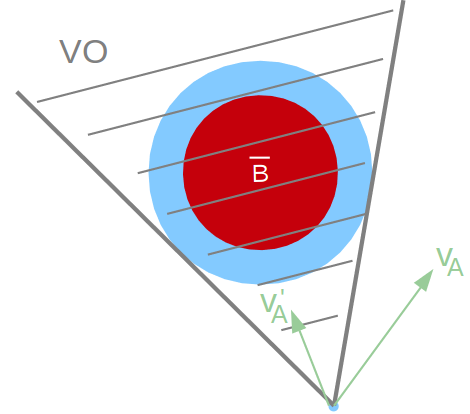
• VO是指速度方向与B¯B¯相交的部分，即会发生碰撞的部分（图中灰色斜线部分）。

• VO是抱着宁杀错，不放过的思想，把所有未来有可能会发生碰撞的速度都放弃了。

• 实际上假如仅要求一定时间内不发生碰撞的话，有更多的速度可供选择，比如说上图中的(v′AvA′)。

• 物体A(B)：以pApA为圆心，rArA为半径的点集AA

• 假设B静止：A相对于B的速度，即相对速度vA−vBvA−vB

• 把A化作质点：求集合BB与集合−A−A的Minkowski
  sum，即闵氏和，B⊕−AB⊕−A，其中

• A⊕B={a+b | a∈A,b∈B}A⊕B={a+b | a∈A,b∈B}

• −A={−a | a∈A}−A={−a | a∈A}

• 更多关于Minkowski
  sum

• 首先给出射线的定义，用λ(p,v)λ(p,v)表示以点pp为顶点，方向为vv的射线。

• λ(p,v)={p+tv|t≥0}λ(p,v)={p+tv|t≥0}

• 接下来就是VO的定义了，用VOAB(vB)VOBA(vB)表示速度为vBvB的BB对AA的VO

• VOAB(vB)={vA|λ(pA,vA−vB)∩B⊕−A≠∅}VOBA(vB)={vA|λ(pA,vA−vB)∩B⊕−A≠∅}

• 抖动现象：如下左图所示，即AA会在vAvA与v′AvA′之间来回切换

• RVO的效果：如下右图所示，保持vAvA，不会抖动

• Symmetry：vAvA的AA会撞上vBvB的BB，则vBvB的BB也会撞上vAvA的AA

• vA∈VOAB(vB)⇔vB∈VOBA(vA)vA∈VOBA(vB)⇔vB∈VOAB(vA)

• Translation Invariance：vAvA的AA会撞上vBvB的BB，则vA+uvA+u的AA会撞上vB+uvB+u的BB

• vA∈VOAB(vB)⇔vA+u∈VOAB(vB+u)vA∈VOBA(vB)⇔vA+u∈VOBA(vB+u)

• Convexity：在VOAB(vB)VOBA(vB)的左（右）侧的两个速度之间的任意速度，也在VOAB(vB)VOBA(vB)的左（右）侧。VO左（右）侧如下图所示：

• vA∉→VOAB(vB)∧v′A∉→VOAB(vB)⇒(1−α)vA+αv′A∉→VOAB(vB), for 0≤α≤1vA∉→VOBA(vB)∧vA′∉→VOBA(vB)⇒(1−α)vA+αvA′∉→VOBA(vB), for 0≤α≤1

1. 假设初始状态为会发生碰撞：vA∈VOAB(vB), vB∈VOBA(vA)vA∈VOBA(vB), vB∈VOAB(vA)

1. 由于在对方的VO内，所以各自选择新的速度以防止碰撞：v′A∉VOAB(vB), v′B∉VOBA(vA)vA′∉VOBA(vB), vB′∉VOAB(vA)

1. 由前面VO的Symmetry性质可知：此时，原来的速度不在当前速度的VO内：vB∉VOBA(v′A), vA∉VOAB(v′B)vB∉VOAB(vA′), vA∉VOBA(vB′)

1. 假设我们更加prefer原来的速度，则又会回到原来的vAvA与vBvB

1. 于是在1→4之间循环，即发生抖动

• 缩小VO的大小，新的”VO”就叫做RVO

• p.s. 我个人对Reciprocal的理解是：相对于VO完全把对方当做木头，RVO假设对方在避障中也会承担一定责任，所以不用完全靠自己改变速度来走出VO，有种互相合作避障的感觉。

• 或者换一个角度理解，不再直接选择VO外的速度v′AvA′作为新的速度，而是average当前速度vAvA与VO外的速度v′AvA′

• 速度为vBvB的BB对速度为vAvA的AA产生的RVO为：

• 图示理解如下：

• 释意：

• 2v′A−vA2vA′−vA：vAvA相对于v′AvA′的对称点。

• 所以公式的含义是：对称点在原VO中，则中点在RVO中。

• 所以RVO的构成是：vAvA与原VO中的点的中点。

• 双方选择同侧避障时，不会发生碰撞。

• 双方一定会选择同侧避障。

• 不会有抖动现象：原来会撞的在选择新速度后依然会撞。

• 用数学语言来描述问题：化作质点的描述、抖动的描述。

• 从实际应用中发现问题：抖动问题的发现。

• 特殊到一般的推广：论文后面还将RVO推广到一般情况，很漂亮的推广。

• Reciprocal Velocity Obstacles for Real-Time
  Multi-Agent Navigation

• Minkowski
  Sums

很容易可以跟我们的日常生活进行类比，比如说我们要从学校的教学楼走到宿舍楼，那么以上框架对应的就是：

VO和RVO就是经典的底层避障算法。其中VO是最经典的，RVO则在VO的基础上进行了一些改进，解决了VO抖动的问题。

VO(Velocity Obstacle)

一句话总结VO的思路：只要在未来有可能会发生碰撞的速度，都排除在外。

为方便描述，以下都假设是在平面内，圆形物体之间的避障。

VO的直观理解

问题描述

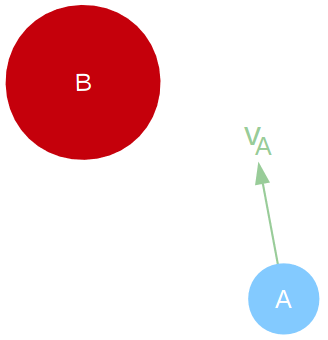
Q: 假设B静止，那么A取什么速度能够保证一定不会跟B发生碰撞呢？

A: 一种很粗暴的方法，就是把A化作质点，选择跟B¯B¯(扩展后的B)不相交的速度方向。以后只要在每个周期里面，都选择不在VO的速度，就能够保证不会碰撞。

解决办法

以上就是VO的直观理解，需要注意的是：

VO的图示理解

有了直观理解之后就可以用更加严谨一点的数学语言图示VO了。

首先将直观理解中口语化的表达转换成对应的数学语言表示。

于是就有了下图的左半部分（浅色三角形）：

而为了直接求vAvA绝对速度的VO而不是vA−vBvA−vB相对速度的VO，将相对速度下的VO延vBvB方向平移，就有了图中右半部分（深色三角形）。

VO的数学定义

理解了图示，数学定义就很好理解了。

RVO(Reciprocal Velocity Obstacle)

VO给出了很漂亮的避障条件，所以后面很多底层的避障算法都是基于VO的，而RVO就是其中之一。

RVO主要解决了VO的抖动问题

证明VO抖动现象存在

首先论文给出了VO的三条性质

VO左（右）侧示意

接下来是抖动现象存在的证明

RVO的Insight

首先回想一下为什么会发生抖动：

双方为了避障，都偏移了当前速度太多，导致更新速度后，原来速度不再会发生碰撞。

那么我们有没有办法减少对当前速度的偏移，同时又能保证避障呢，RVO的回答是肯定的：

RVO的定义与图示

RVOAB(vB,vA)={v′A | 2v′A−vA∈VOAB(vB)}RVOBA(vB,vA)={vA′ | 2vA′−vA∈VOBA(vB)}

RVO不会发生碰撞且没有抖动现象的证明

这一部分不赘述了，论文中写得很详尽，只说一下证明的思路：

收获

References