docker的通俗理解

自己买了个服务器，前不久搭建好的一个网站，想要再搞一个站点，无奈只能修改端口后，再部署另外一个站点。繁琐的配置运行环境，迁移网站，是否让你感觉到很繁琐?服务器不想用了，想搬迁到另外一台服务器去部署，先是拷贝原有数据，在新的服务器上又开始搭建环境进行部署，这些费时间的事情现在只需要几分钟就能完成，那就是docker技术。

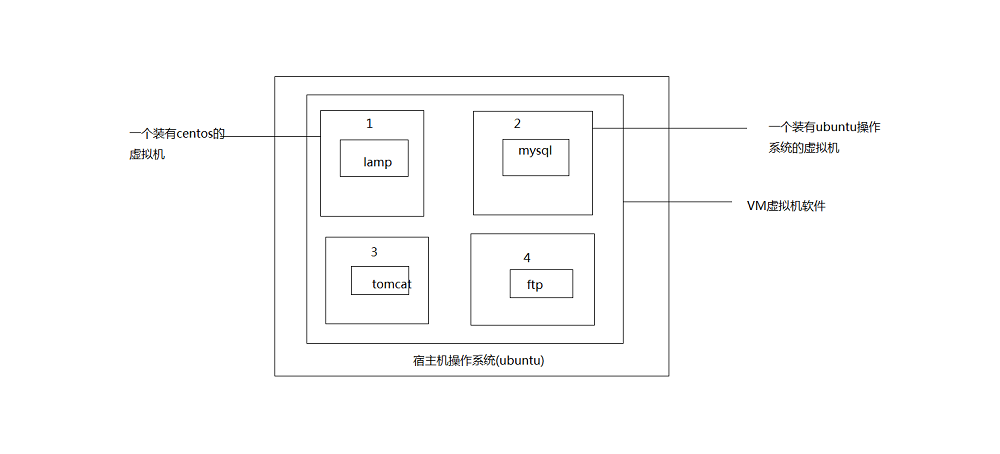
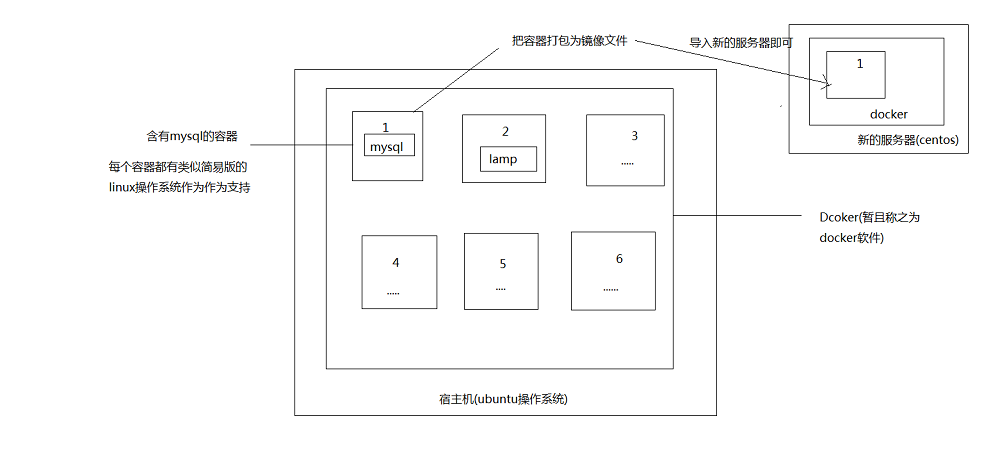
docker通俗按照自己的理解来说，就是类似VM虚拟机一样的虚拟技术。但是它比虚拟机更加强大，体积小，运行速度快，启动和关闭只需要几秒。相对于普通虚拟机来说，启动时间在分钟级别，占用内存大。所以这就是docker出现之后的优势。docker容器可以打包为镜像文件(类似VM虚拟机的那些快照文件)，迁移的时候我们只需要在新服务器上安装docker,就能把之前打包好的镜像文件导入到docker里面，运行容器，就能实现访问，不需要重新配置环境。下面一张图展示普通虚拟机和docker的区别。

  VM虚拟机:

        docker架构图:

我们进行对比一下，docker其实就是和虚拟机的目的差不多，都是虚拟化技术。但是docker比虚拟机更加轻量级，更快，更加易于移植。

    镜像:  创建虚拟机和docker 都必不可少的东西。  用过虚拟机的朋友都知道，创建一个虚拟机就先得下载操作系统的ISO镜像文件，然后通过镜像文件安装操作系统，和实体机类似，然后能在虚拟机中去安装各种软件。

  容器:  通俗拿VM虚拟机和docker来举例，一个容器就类似于一个虚拟机，只不过在docker技术的术语上称为容器。这个容器装的就是我们部署的应用在运行，和虚拟机一样可以开机，关机，重启。docker称为容器的运行，关闭，重启。而且这个容器可以打包为镜像文件，类似虚拟机快照的文件，放在其它虚拟机上又可以保持原样能运行，docker也是如此，把容器打包为镜像文件，然后在新的服务器安装好的docker环境下导入进去，保持原来的状态能够运行。

透过现象看本质：

1、docker容器实际上就是运行的一个进程，只不过由于docker帮助我们包装了这个进程，给这个进程加以一个可运行的微linux环境而已，让我们感觉看起来"像"虚拟机而已。所以也就不奇怪，为什么容器的启动是秒级的，启动一个虚拟机是分钟级别的。

2.  举个简单例子。一个房子比较大，假如租户一起住，大家一起住难免有束缚感,也不太方便。那么房东把房子改造一下，房子用可拆装的墙板隔离开来，分为许多的小房间，每个人住在自己的小房间。小房间麻雀虽小，五张俱全,你可以自己布置自己的房间。每个租客在自己的"小房间"里面可以做自己的事情，从而也不会打扰到其他人。但是他们都是共享这个房子的水费，电费，网费等公共资源(每个docker容器(也就是进程)依赖的是宿主机的资源)。  聪明的你会想到， 可拆装的墙板隔音效果或安全性不够(docker容器之间的隔离性比真实虚拟机要稍微弱)， 会不会有坏人打个洞偷窥？  会不会有人监听我在房间的一举一动?  可拆装的墙板肯定是不比水泥墙(虚拟机隔离性)牢固.虽说隔离性没有虚拟机那么强，但是目前为止docker还没暴露出关于这方面的问题，广泛的社区以及大厂Google等公司都在使用，所以我们还是可以放心大胆使用的。   假如有一天房东要把房子卖了，只要把可拆装的墙板移除，打扫一下，回到原样，不破坏房子原样，就可以出售房子了(在容器中安装的软件，程序等都不会污染到宿主机的环境，容器被删除也就被删除了)。

原文地理：https://blog.csdn.net/xyz_dream/article/details/53081687