HDU 5358 First One 求和（序列求和，优化）

题意：给定一个含n个元素的序列，求下式子的结果。S(i,j)表示为seq[i...j]之和。注：对于log₂⁰可视为1。数据量n<=10⁵。

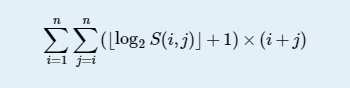
思路：即使能够在O(1)的时间内求得任意S，也是需要O(n*n)来求和的。

　　对于这种题，一般就是研究式子，看有什么办法可以减少复杂度。

　　看到式子中的向下取整符号了吗？很多数的取整结果是相同的，即使给个2147483647取整也只是30多而已（噗，忘了多少）。

　　而对于这个式子，S最大也不会超过longlong，确切计算，小于2³⁴。那么取log之后的范围这么小，如果能够知道分别有多少个的话，那就快多了。可以看得出对于同一个i，取log后的结果是呈线性的，从1到34逐步递增的（当然有可能没有那么大/小）。

　　那很好办，对于每个i，只需要将一整段“取log后向下取整的结果加1”为k的给截出来，统计k个（i,j）之和再乘以k不就是这一段的答案了吗？那么对于每个i，最多可能被截成34段啦。相比而言快了许多。复杂度为O(34*n)。

　　但是本题连这样的复杂度还是不行，还能继续优化，设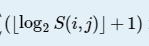为k。

　　（1）先穷举k，k=[1,34].

　　（2）再穷举i。对于每个i，假设i-1中(i-1, R)这一段的结果为k，而i中答案为k的对应段必定大于等于这段（为什么？小学老师教的序列求和技术）。所以只需从上次穷举完之处继续往后判断即可，因为i比i-1少了个数字，说不定就变小了许多，再加几个不就补回来啦！

　　再具体的话就很难说清了，看代码注释吧。我看得懂相信你也可以。

 #include <bits/stdc++.h>
 #define INF 0x7f7f7f7f
 #define pii pair<int,int>
 #define LL long long
 using namespace std;
 const int N=;
 LL sum[N], up[];
 int cur[N];
 void pre_cal()
 {
     sum[]=;
     for(int i=; i<; i++)    up[i]= (LL)<<i;
 }
 LL cal(int n)
 {
     for(int i=; i<=n; i++) cur[i]=i;   //记录以i为下标的，穷举到那里了。

     LL ans=;
     int L=, R=;
     for(int k=; k<; k++)
     {
         R=cur[];
         for(int i=; i<=n; i++) //以i为下标的
         {
             L=cur[i];
             R=max(cur[i], cur[i-]);     //这一步决定了AC或者TLE
             if(L>n) continue;            //以i为下标的已经计算完毕。

             while( R<=n &&  sum[R]-sum[i-]<up[k] )    R++;     //找到（logx+1）为k的一段[L,R)
             if(L<R)
             {
                 cur[i]=R;
                 if((R-L)&)          ans+=( (LL)(R-L)*i + (LL)(R-+L)/*(R-L) )*max(,k);   //注意这里千万要转longlong
                 else                 ans+=( (LL)(R-L)*i + (LL)(R-+L)*(R-L)/ )*max(,k);
             }
         }
     }

     return ans;
 }

 int main()
 {
     freopen("input.txt", "r", stdin);
     pre_cal();
     int t, n;
     scanf("%d", &t);
     while(t--)
     {
         scanf("%d", &n);
         for(int i=; i<=n; i++)
         {
             scanf("%lld", &sum[i]);
             sum[i] += sum[i-];
         }
         printf("%lld\n", cal(n));
     }
     return ;
 }

AC代码