Uva 1220，Hali-Bula 的晚会

题目链接：https://uva.onlinejudge.org/external/12/1220.pdf

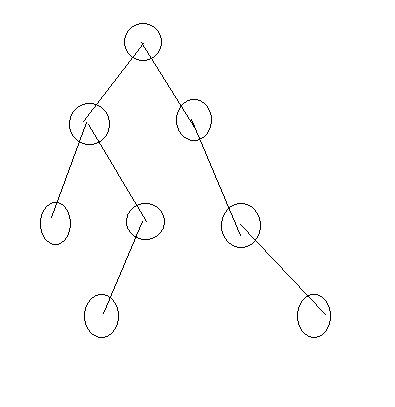
题意： 公司n个人，形成一个数状结构，选出最大独立集，并且看是否是唯一解。

分析：

d(i) 是 节点 i 的最优值， i 只有两种决策，就是选和不选。 转移方程：

d(i) = max {1+Σ₁d(j),Σ₂d(j)}; Σ₁是所有孙子节点，Σ₂是所有儿子节点。

那么状态的定义d(i,0),节点 i 不选，d(i,1)，节点 i 选。

那么状态转移方程就是：

是否唯一 f(v,0) = 1 表示唯一， f(v,1) = 0 不唯一。

d(u,1) = sum{d(v,0)}（v是u的子节点），当所有 f(v,0) = 1,d(u,1) = 1;

d(u,0) = sum{max(d(v,0),d(v,1))}, if (d(v,0)==d(v,1)) f(u,0) = 0,取的对应的f()==0,f(u,0) = 0;

存树形结构，一个较好的方式用邻接表，每个字符串对应一个ID，可以用map<string,int>dict，有一个较好的函数，dict.count(s)，s字符串出现的次数。

#include <bits/stdc++.h>
using namespace std;

const int maxn = +;
int cnt;
int n;
vector<int> sons[maxn];
int d[maxn][],f[maxn][];

map<string,int> dict;

int ID(const string &s) {
    if(!dict.count(s)) dict[s] = cnt++;
    return dict[s];
}

int dp(int u,int k) {
    f[u][k] = ;
    d[u][k] = k;
    for(int i=;i<sons[u].size();i++) {
        int v = sons[u][i];
        if(k==) {
            d[u][] +=dp(v,);
            if(!f[v][]) f[u][] = ;
        }
        else {
            d[u][] +=max(dp(v,),dp(v,));
            if(d[v][]==d[v][]) f[u][k] = ;
            else if(d[v][]>d[v][]&&!f[v][]) f[u][k] = ;
            else if(d[v][]>d[v][]&&!f[v][]) f[u][k] = ;
        }
    }
    return d[u][k];
}

int main()
{
    string s,s2;
    while(cin>>n>>s) {
        cnt = ;
        dict.clear();

        for(int i=;i<n;i++)
            sons[i].clear();

        ID(s);
        for(int i=;i<n-;i++) {
            cin>>s>>s2;
            sons[ID(s2)].push_back(ID(s));
        }

        printf("%d ",max(dp(,),dp(,)));
        bool unique = false;
        if(d[][]>d[][]&&f[][]) unique = true;
        if(d[][]>d[][]&&f[][]) unique = true;
        if(unique) printf("Yes\n");
        else printf("No\n");

    }

    return ;
}