softmax 损失函数求导过程

前言：softmax中的求导包含矩阵与向量的求导关系，记录的目的是为了回顾。

　　下图为利用softmax对样本进行k分类的问题，其损失函数的表达式为结构风险，第二项是模型结构的正则化项。

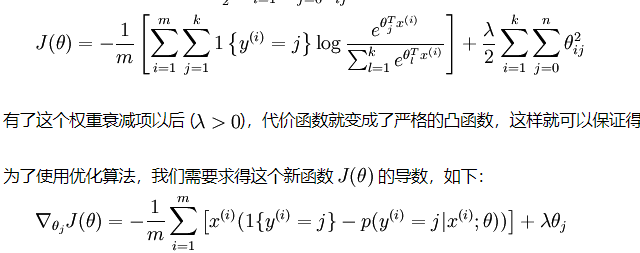
　　首先，每个queue：x(i)的特征维度是 n , 参数 θ 是一个 n×k 的矩阵，输出的结果 y(i) 为一个 k×1 的向量，其中第 j 个元素对应元素的 e 指数为该 queue 属于第 j 类的概率(未归一化)。所以虽然损失函数 J(θ) 是一个常数，但是它的自变量为一个矩阵 Θ 和 一个特征向量 x(i) ，这就牵涉到本文的重难点：矩阵、向量以及变量之间的求导。

　　更新 θj 的过程就是标量 J(θ) 对向量  θj 求导的过程，向量对标量求导的具体方式不想写，结论见文末，参考（https://blog.csdn.net/daaikuaichuan/article/details/80620518）。

　　

　　第一项的求导过程：

　　　　将与 j 无关的乘项（-1/m)×∑_i ×1{ j } 拉到最前面，对log中内容做变换得到（(θ_j×x⁽ⁱ⁾)) - log(∑L)。前者根据变量对向量求导可以得到为x(i),后者根据链式法则可以求出为{ [exp(θj*x(i)] / ∑L}* x(i), 与前面的项相乘就可以得到下式中的第一项。

　　第二项为 Θ 中所有列向量二范数之和，可以写成 ∑θjTθj ，其中与 θj 有关的内容为 θj^Tθj ，求导后为  2θj 。求导的结果为第二项。

　　 J(θ) 对 θj 求导的结果如文中第二式。

标量对向量求导

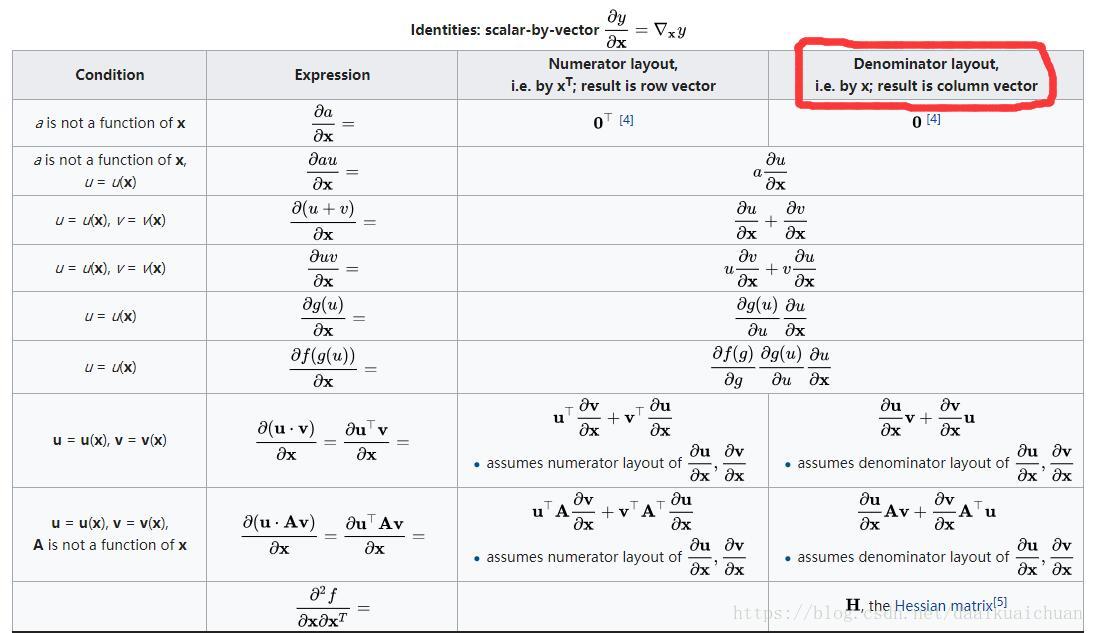
向量对标量求导

向量对向量求导