L1-060 心理阴影面积

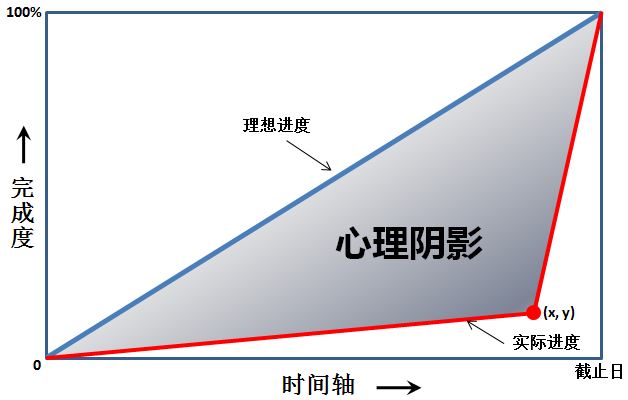
这是一幅心理阴影面积图。我们都以为自己可以匀速前进（图中蓝色直线），而拖延症晚期的我们往往执行的是最后时刻的疯狂赶工（图中的红色折线）。由红、蓝线围出的面积，就是我们在做作业时的心理阴影面积。

现给出红色拐点的坐标 (，要求你算出这个心理阴影面积。

输入格式：

输入在一行中给出 2 个不超过 100 的正整数 x 和 y，并且保证有 x>y。这里假设横、纵坐标的最大值（即截止日和最终完成度）都是 100。

输出格式：

在一行中输出心理阴影面积。

友情提醒：三角形的面积 = 底边长 x 高 / 2；矩形面积 = 底边长 x 高。嫑想得太复杂，这是一道 5 分考减法的题……

输入样例：

90 10

输出样例：

4000

 

思路：小学数学题，略水略水......

 

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<algorithm>
 #include<map>
 #include<set>
 #include<vector>
 using namespace std;
 #define ll long long
 #define dd cout<<endl
 const int inf=;
 const int mod=1e9+;
 const int maxn=1e5+;
 int main()
 {
     int x,y;
     cin>>x>>y;
     int area=*/-x*y/-(-x)*y-(-x)*(-y)/;
     cout<<area<<endl;
     return ;
 }