一个简单的统计问题（解决方案：Trie树）

题目如图

  输入几个不重复的单词和几个前缀，分别统计出单词中包含前缀的个数。

Trie树

  这个题目用到了 Trie 树.它在百度百科中的定义如下：在计算机科学中，Trie，又称字典树、单词查找树或键树，是一种树形结构，是一种哈希树的变种。典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串），所以经常被搜索引擎系统用于文本词频统计。它的优点是：利用字符串的公共前缀来减少查询时间，最大限度地减少无谓的字符串比较，查询效率比哈希树高。Trie的核心思想是空间换时间，利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的。它有3个基本性质：根节点不包含字符，除根节点外每一个节点都只包含一个字符。从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。每个节点的所有子节点包含的字符都不相同。

代码示例

package algorithm.tree;
public class Trie {
    class Node {
        char value;
        byte end = 0;
        Node[] next = new Node[26];
        int count;
    }
    private Node root;
    public Trie() {
        root = new Node();
    }
    public boolean put(String value) {
        if (value == null || value.isEmpty()) {
            return false;
        }
        Node p = root;
        int index;
        char[] values = value.toCharArray();
        for (int i = 0; i < values.length; i++) {
            index = values[i] - 'a';
            if (p.next[index] == null) {
                Node node = new Node();
                node.value = values[i];
                p.next[index] = node;
            }
            p = p.next[index];
            p.end = 0;
            p.count++;
        }
        p.end = 1;
        return true;
    }
    public boolean find(String value,boolean pattern) {
        if (value == null || value.isEmpty()) {
            return false;
        }
        Node p = root;
        char[] values = value.toCharArray();
        for (int i = 0; i < values.length; i++) {
            int index = values[i] - 'a';
            if (p.next[index] == null) {
                return false;
            }
            p = p.next[index];
        }
        return pattern ? true : p.end == 1;
    }
    public int count(String value) {
        if (value == null || value.isEmpty()) {
            return 0;
        }
        Node p = root;
        char[] values = value.toCharArray();
        for (int i = 0; i < values.length; i++) {
            int index = values[i] - 'a';
            if (p.next[index] == null) {
                return 0;
            }
            p = p.next[index];
        }
        return p.count;
    }
}

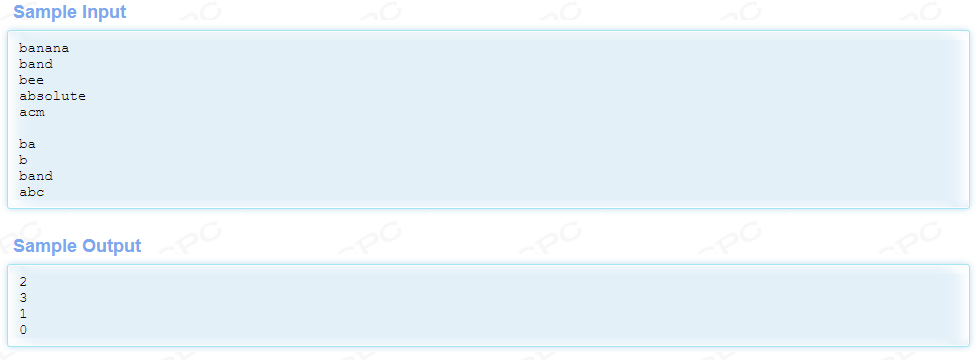
测试

    public static void main(String[] args) {
        Trie trie = new Trie();
        trie.put("banana");
        trie.put("band");
        trie.put("bee");
        trie.put("absolute");
        trie.put("acm");
        //2
        int count1 = trie.count("ba");
        //3
        int count2 = trie.count("b");
        //1
        int count3 = trie.count("band");
        //0
        int count4 = trie.count("abc");
    }