hihoCoder #1190 : 连通性·四（点的双连通分量模板）

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

小Hi和小Ho从约翰家回到学校时，网络所的老师又找到了小Hi和小Ho。

老师告诉小Hi和小Ho：之前的分组出了点问题，当服务器(上次是连接)发生宕机的时候，在同一组的服务器有可能连接不上，所以他们希望重新进行一次分组。这一次老师希望对连接进行分组，并把一个组内的所有连接关联的服务器也视为这个组内的服务器(注意一个服务器可能属于多个组)。

这一次的条件是对于同一个组满足：当组内任意一个服务器宕机之后，不会影响组内其他服务器的连通性。在满足以上条件下，每个组内的边数量越多越好。

比如下面这个例子，一共有6个服务器和7条连接：

其中包含3个组，分别为{(1,2),(2,3),(3,1)},{(4,5),(5,6),(4,6)},{(3,4)}。对{(1,2),(2,3),(3,1)}而言，和该组边相关联的有{1,2,3}三个服务器：当1宕机后，仍然有2-3可以连接2和3；当2宕机后，仍然有1-3可以连接1和3；当3宕机后，仍然有1-2可以连接1和2。

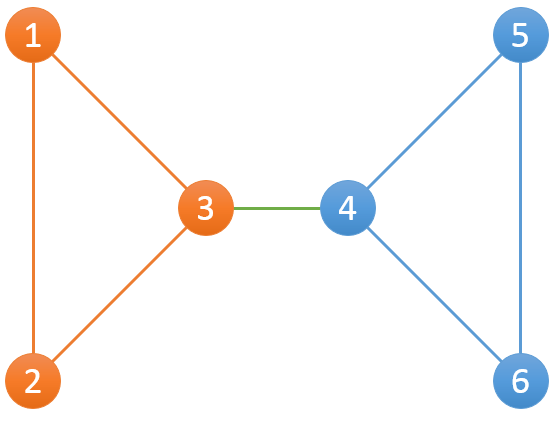
老师把整个网络的情况告诉了小Hi和小Ho，希望小Hi和小Ho统计一下一共有多少个分组。

提示：点的双连通分量

输入

第1行：2个正整数，N,M。表示点的数量N，边的数量M。1≤N≤20,000, 1≤M≤100,000

第2..M+1行：2个正整数，u,v。第i+1行表示存在一条边(u,v)，编号为i，连接了u,v两台服务器。1≤u<v≤N

保证输入所有点之间至少有一条连通路径。

输出

第1行：1个整数，表示该网络的连接组数。

第2行：M个整数，第i个数表示第i条连接所属组内，编号最小的连接的编号。比如分为{(1,2)[1],(2,3)[3],(3,1)[2]},{(4,5)[5],(5,6)[7],(4,6)[6]},{(3,4)[4]}，方括号内表示编号，则输出{1,1,1,4,5,5,5}。

代码

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<vector>
 #include<stack>
 #include<algorithm>
 using namespace std;
 const int N=2e4+;            //最大点数
 const int M=1e5+;            //最大边数

 struct node{
     int id,to;
     node(int id,int to):id(id),to(to){}
 };
 vector<node>v[N];
 stack<int>sk;
 int cnt,num;
 int low[N],dfn[N],fa[M],mp[M];
 //fa[i]为第i条边所属的点双连通分量编号
 //mp[i]为编号为i的点双连通分量里编号最小的编号
 //一定注意fa和mp的范围是边数的范围M,不是点数范围N
 void tarjan(int u,int f){
     low[u]=dfn[u]=++cnt;
     for(int i=;i<v[u].size();i++){
         int t=v[u][i].to;
         int id=v[u][i].id;
         if(t==f) continue;
         if(!dfn[t]){         //树边
             sk.push(id);    //边入栈
             tarjan(t,u);
             low[u]=min(low[u],low[t]);
             if(dfn[u]<=low[t]){
                 num++;
                 while(!sk.empty()){
                     int cur=sk.top();
                     sk.pop();
                     fa[cur]=num;
                     if(mp[num]==||mp[num]>cur)
                         mp[num]=cur;
                     if(cur==id) break;
                 }
             }
         }
         else if(dfn[t]<dfn[u]){//回边
             low[u]=min(low[u],dfn[t]);
             sk.push(id);    //边入栈
         }
     }
 }

 int main(){
     int n,m;
     scanf("%d%d",&n,&m);;
     for(int i=;i<=m;i++){
         int a,b;
         scanf("%d%d",&a,&b);
         v[a].push_back(node(i,b));
         v[b].push_back(node(i,a));
     }
     tarjan(,-);
     printf("%d\n",num);
     for(int i=;i<=m;i++){
         printf("%d%c",mp[fa[i]],i==m?'\n':' ');
     }
     return ;
 }