[Bayes] dchisq: Metropolis-Hastings Algorithm

不错的文章：LDA-math-MCMC 和 Gibbs Sampling

可作为精进MCMC抽样方法的学习材料。

简单概率分布的模拟

Box-Muller变换原理详解

本质上来说，计算机只能生产符合均匀分布的采样。如果要生成其他分布的采样，就需要借助一些技巧性的方法，例如我们在前面的文章提到过的逆变换采样、拒绝采样以及自适应的拒绝采样等等。

涉及到 "逆变换" [Bayes] runif: Inversion Sampling

例如：U1, U2是均匀分布，可得到两个高斯分布的变量X, Y。

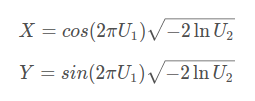
复杂概率分布的模拟

使用的必要性

当p(x)的形式很复杂，或者 p(x) 是个高维的分布的时候，样本的生成就可能很困难了。譬如有如下的情况

- - p(x)=p~(x)∫p~(x)dx,而 p~(x) 我们是可以计算的，但是底下的积分式无法显式计算。
  - p(x,y) 是一个二维的分布函数，这个函数本身计算很困难，但是条件分布 p(x|y),p(y|x)的计算相对简单;如果 p(x) 是高维的，这种情形就更加明显。

此时就需要使用一些更加复杂的随机模拟的方法来生成样本。而本节中将要重点介绍的 MCMC(Markov Chain Monte Carlo) 和 Gibbs Sampling算法就是最常用的一种，这两个方法在现代贝叶斯分析中被广泛使用。要了解这两个算法，我们首先要对马氏链的平稳分布的性质有基本的认识。

马氏链及其平稳分布

平稳性：这个收敛行为主要是由概率转移矩阵P决定的。

自然的，这个收敛现象并非是我们这个马氏链独有的，而是绝大多数马氏链的共同行为，关于马氏链的收敛我们有如下漂亮的定理：

马氏链定理：如果一个非周期马氏链具有转移概率矩阵P,且它的任何两个状态是连通的，那么 limn→∞Pnij 存在且与i无关，记 limn→∞Pnij=π(j), 我们有

1. limn→∞Pn=⎡⎣⎢⎢⎢⎢⎢π(1)π(1)⋯π(1)⋯π(2)π(2)⋯π(2)⋯⋯⋯⋯⋯⋯π(j)π(j)⋯π(j)⋯⋯⋯⋯⋯⋯⎤⎦⎥⎥⎥⎥⎥
2. π(j)=∑i=0∞π(i)Pij
3. π 是方程 πP=π 的唯一非负解

其中, π=[π(1),π(2),⋯,π(j),⋯],∑i=0∞πi=1

π称为马氏链的平稳分布。

这个马氏链的收敛定理非常重要，所有的 MCMC(Markov Chain Monte Carlo) 方法都是以这个定理作为理论基础的。

历史由来

马氏链的平稳分布 --> Metropolis算法

对于给定的概率分布p(x),我们希望能有便捷的方式生成它对应的样本。由于马氏链能收敛到平稳分布，于是一个很的漂亮想法是：如果我们能构造一个转移矩阵为P的马氏链，使得该马氏链的平稳分布恰好是p(x), 那么我们从任何一个初始状态x0出发沿着马氏链转移, 得到一个转移序列 x0,x1,x2,⋯xn,xn+1⋯,，如果马氏链在第n步已经收敛了，于是我们就得到了 π(x) 的样本xn,xn+1⋯。

这个绝妙的想法在1953年被 Metropolis想到了，为了研究粒子系统的平稳性质， Metropolis 考虑了物理学中常见的波尔兹曼分布的采样问题，首次提出了基于马氏链的蒙特卡罗方法，即Metropolis算法，并在最早的计算机上编程实现。Metropolis 算法是首个普适的采样方法，并启发了一系列 MCMC方法，所以人们把它视为随机模拟技术腾飞的起点。 Metropolis的这篇论文被收录在《统计学中的重大突破》中， Metropolis算法也被遴选为二十世纪的十个最重要的算法之一。

改进变种：Metropolis-Hastings 算法

我们接下来介绍的MCMC 算法是 Metropolis 算法的一个改进变种，即常用的 Metropolis-Hastings 算法。

Gibbs Sampling

对于，由于接受率 α的存在(通常 α<1), 以上 Metropolis-Hastings 算法的效率不够高。能否找到一个转移矩阵Q使得接受率 α=1 呢？