Gym 100917J---dir -C（RMQ--ST）

题目链接

http://codeforces.com/gym/100917/problem/D

problem description

Famous Berland coder and IT manager Linus Gates announced his next proprietary open-source system "Winux 10.04 LTS"

In this system command "dir -C" prints list of all files in the current catalog in multicolumn mode.

Lets define the multicolumn mode for number of lines l. Assume that filenames are already sorted lexicographically.

• We split list of filenames into several continuous blocks such as all blocks except for maybe last one consist of l filenames, and last block consists of no more than l filenames, then blocks are printed as columns.
• Width of each column wi is defined as maximal length of the filename in appropriate block.
• Columns are separated by 1 × l column of spaces.
• So, width of the output is calculated as 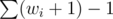, i.e. sum of widths of each column plus number of columns minus one.

Example of multi-column output:

a       accd e t
aba     b    f wtrt
abacaba db   k

In the example above width of output is equal to 19.

"dir -C" command selects minimal l, such that width of the output does not exceed width of screen w.

Given information about filename lengths and width of screen, calculate number of lines l printed by "dir -C" command.

Input

First line of the input contains two integers n and w — number of files in the list and width of screen (1 ≤ n ≤ 105, 1 ≤ w ≤ 109).

Second line contains n integers fi — lengths of filenames. i-th of those integers represents length of i-th filename in the lexicographically ordered list (1 ≤ fi ≤ w).

Output

Print one integer — number of lines l, printed by "dir -C" command.

Examples

input

11 20
1 3 7 4 1 2 1 1 1 1 4

output

3

题意：有n个目录名字符串，长度为a[1]~a[n] 屏幕宽为w  ，现在要按照已经给的目录循序一列一列的放，每一列放x个，最后一列放<=x个  要求每一列目录名左端对整齐 ，形成一个长方形的块 ，且块与块之间空一格，且不能超过屏幕的宽度，求最小的行数；

思路：先对输入长度处理，用ST算出每个区间的最大值，然后枚举行数x 从1 ~ n；

代码如下：

#include <iostream>
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <map>
#include <cmath>
using namespace std;
typedef long long LL;
const int MAXN = 1e5+;
int a[MAXN],m[][MAXN];
int n;
LL w;

int main()
{
    while(scanf("%d%I64d",&n,&w)!=EOF)
    {
         memset(m,,sizeof(m));
         for(int i=;i<=n;i++)
         {
             scanf("%d",&a[i]);
             m[][i]=a[i];
         }
         for(int i=;i<=(int)log(n)/log();i++)
         {
             for(int j=;j+(<<i)-<=n;j++)
                m[i][j]=max(m[i-][j],m[i-][j+(<<(i-))]);
         }

         for(int i=;i<=n;i++)
         {
             int k=(int)log(i);
             long long sum=;
             for(int j=;j<n/i;j++)
             {
                 sum+=(long long)max(m[k][j*i+],m[k][i*(j+)-(<<k)+])+;
             }
             if(n%i!=) {
                k=(int)log(n%i);
                sum+=(long long)max(m[k][n-n%i+],m[k][n-(<<k)+])+;
             }
             if(sum-<=w){
                printf("%d\n",i);
                break;
             }
         }
    }
    return ;
}