2019.2.21 T2题解

meet

大概思路就是 ， 找出相交的路径 ， 判断方向 ， 分类讨论。。

假设已经找出了相交路径 。。。

若方向相同 ， 则找到相交路径上边权的最大值 ， 若最大值>出发时间差 ， 则可行。

原因： 由于方向相同所以在相交路径上这两个点的相对距离是不变的，看最大的边权即可。

这个东西用st表就可以搞定

若方向不同，就看看他们相遇的位置是不是相交路径上各个（不一定是最两头的点）边的端点之一。

因为题中说在边上才算 ， 点不能算到边上。 所以不在点上就一定会在边上相遇。

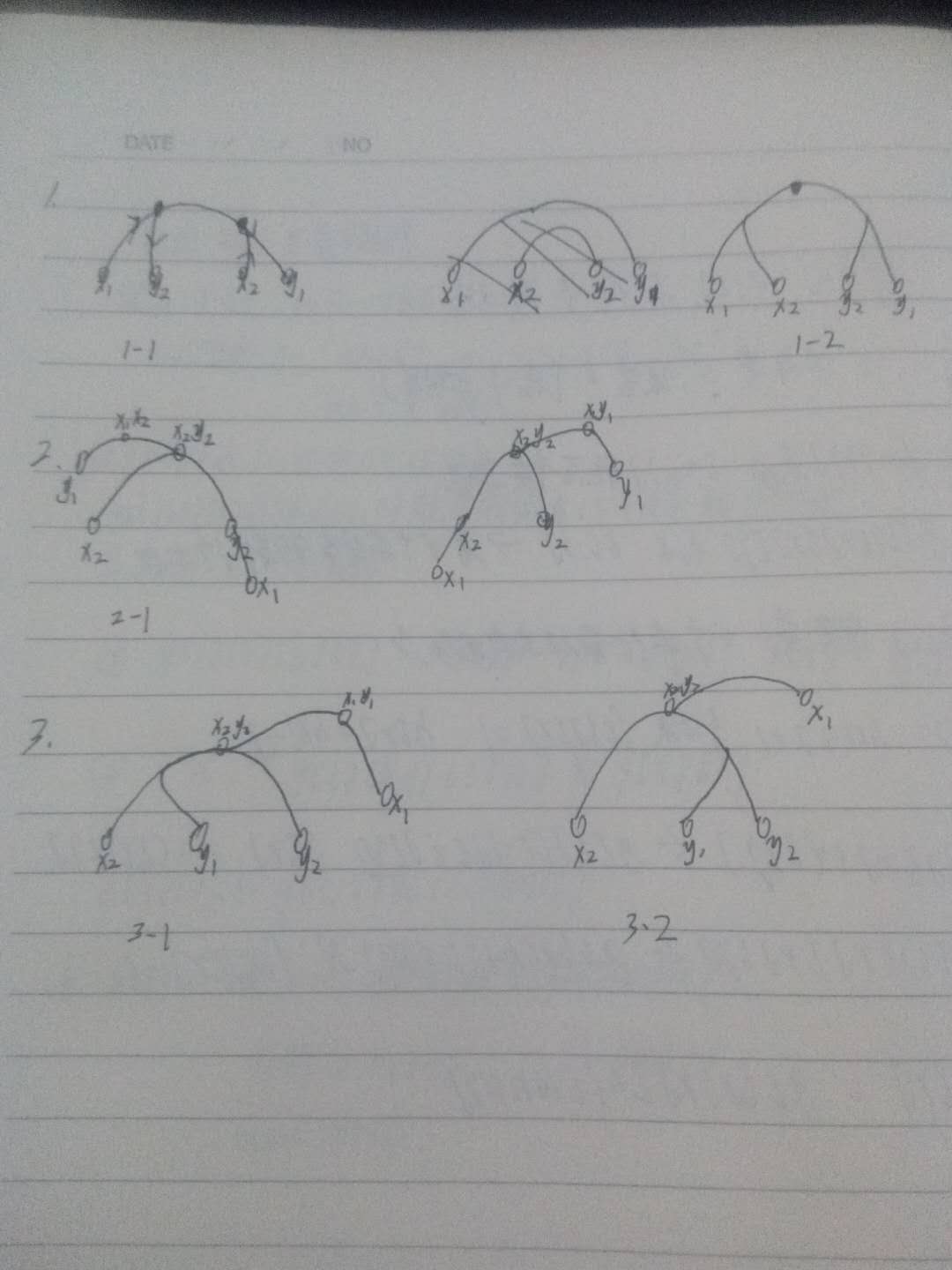
然后就是怎么找相交路径了。。

大概有这么几种情况。。

分类讨论即可

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#include<vector>
#include<cmath>
#include<queue>
#include<set>
#include<map>
using namespace std;
#define int long long
const int N = 1e5+10;
inline int read()
{
    register int x = 0 , f = 0; register char c = getchar();
    while(c < '0' || c > '9') f |= c == '-' , c = getchar();
    while(c >= '0' && c <= '9') x = (x << 3) + (x << 1) + c - '0' , c = getchar();
    return f ? -x : x;
}
int n , Q , cnt;
int head[N] , f[N][20] , st[N][20] , pre[N] , d[N] , dis[N] , Log[N];
struct edge{ int v , nex , c , id; } e[N<<1];
struct node{
	int id , l , r;
	node(int id = 0 , int l = 0 , int r = 0) : id(id) , l(l) , r(r) {}
} A[N] , B[N];
inline void add(int u , int v , int c , int id) { e[++cnt].v = v; e[cnt].nex = head[u]; e[cnt].c = c;  e[cnt].id = id; head[u] = cnt; return ; }

void dfs(int x , int fa)
{
	f[x][0] = fa; d[x] = d[fa] + 1;
	for(int i = 1 ; i < 20 ; ++i) f[x][i] = f[f[x][i-1]][i-1] , st[x][i] = max(st[x][i-1] , st[f[x][i-1]][i-1]);
	for(int i = head[x] , v ; i ; i = e[i].nex)
	{
		v = e[i].v; if(v == fa) continue;
		pre[v] = i; st[v][0] = e[i].c; dis[v] = dis[x] + e[i].c; dfs(v , x);
	}
	return ;
}

int LCA(int x , int y)
{
	if(d[x] < d[y]) swap(x , y);
	for(int i = 19 ; ~i ; --i) if(d[f[x][i]] >= d[y]) x = f[x][i];
	if(x == y) return x;
	for(int i = 19 ; ~i ; --i) if(f[x][i] != f[y][i]) x = f[x][i] , y = f[y][i];
	return f[x][0];
}

void Work(int u , int v , int t , int &tot , node *s)
{
	int p = LCA(u , v);
	while(u != p)
	{
		int i = pre[u];
		s[++tot] = node(e[i].id , t , t + e[i].c);
		t += e[i].c; u = f[u][0];
	}
	int lim = tot , T = 0;
	while(v != p)
	{
		int i = pre[v];
		s[++tot] = node(e[i].id , T , T + e[i].c);
		T += e[i].c; t += e[i].c; v = f[v][0];
	}
	for(int i = lim + 1 ; i <= tot ; ++i) s[i].l = t - s[i].l , s[i].r = t - s[i].r , swap(s[i].l , s[i].r);
	return ;
}

inline bool cmp(const node &A , const node &B) { return A.id < B.id; }

void solve1()
{
	for(int i = 1 ; i <= n ; ++i) d[i] = 0;
	dfs(1 , 0);
	int u1 , v1 , t1 , u2 , v2 , t2 , tot1 , tot2;
	while(Q--)
	{
		u1 = read(); v1 = read(); t1 = read(); tot1 = 0;
		u2 = read(); v2 = read(); t2 = read(); tot2 = 0;
		Work(u1 , v1 , t1 , tot1 , A);
		Work(u2 , v2 , t2 , tot2 , B);
		sort(A + 1 , A + 1 + tot1 , cmp);
		sort(B + 1 , B + 1 + tot2 , cmp);
		int l = 1 , r = 1 , flag = 0;
		while(l <= tot1 && r <= tot2)
		{
			if(A[l].id < B[r].id) l++;
			else if(A[l].id > B[r].id) r++;
			else
			{
				if((A[l].l <= B[r].l && B[r].l < A[l].r) || (A[l].l < B[r].r && B[r].r <= A[l].r)) { flag = 1; break; }
				l++; r++;
			}
		}
		puts(flag ? "YES" : "NO");
	}
	return ;
}

int Ask_MAX(int x , int y) // 求得x->y之间边权的最大值
{
	int ans = 0;
	if(d[x] < d[y]) swap(x , y);
	for(int i = 19 ; ~i ; --i) if(d[f[x][i]] >= d[y]) ans = max(ans , st[x][i]) , x = f[x][i];
	if(x == y) return ans;
	for(int i = 19 ; ~i ; --i) if(f[x][i] != f[y][i]) ans = max(ans , max(st[x][i] , st[y][i])) , x = f[x][i] , y = f[y][i];
	return max(ans , max(st[x][0] , st[y][0]));
}

inline int Abs(int x) { return x < 0 ? -x : x; }

#define stop { puts("NO"); return ; }
#define is_ok { puts("YES"); return ; }
void calc0(int x , int y , int t1 , int t2) // 同向
{
	if(x == y) stop
	int Max = Ask_MAX(x , y);
	puts(Abs(t1 - t2) < Max ? "YES" : "NO");
	return ;
}

int find(int x , int s) // x 往上走 s 到达的点是不是整点
{
	s = dis[x] - s;
	for(int i = 19 ; ~i ; --i) if(dis[f[x][i]] >= s) x = f[x][i];
	return dis[x] == s;
}

void calc1(int x , int y , int t1 , int t2)
{
	if(x == y) stop
	int p = LCA(x , y) , s = dis[x] + dis[y] - 2 * dis[p] , S = s + t2 - t1; // 这里的S是用来算x要走多少
	if(S < 0 || S > 2 * s) stop
	if(S & 1) is_ok
	S >>= 1; int ans = 0; // 这是真正x要走多少 ， 上面那个意会。。
	if(dis[x] - dis[p] >= S) ans = find(x , S); else ans = find(y , s - S);
	puts(ans ? "NO" : "YES"); return ;

}

void solve2()
{
	dfs(1 , 0); int x1 , y1 , x2 , y2 , t1 , t2 , lx1x2 , ly1y2 , lx1y1 , lx2y2 , lx1y2 , ly1x2;
	// 各种LCA 很清楚吧
	while(Q--)
	{
		x1 = read(); y1 = read(); t1 = read();
		x2 = read(); y2 = read(); t2 = read();
		lx1y1 = LCA(x1 , y1); lx2y2 = LCA(x2 , y2);
		if(d[lx1y1] > d[lx2y2]) // 让x1y1的LCA在上面
			swap(x1 , x2), swap(y1 , y2), swap(t1 , t2), swap(lx1y1 , lx2y2);

		lx1x2 = LCA(x1 , x2); ly1y2 = LCA(y1 , y2); // 这个要写下面， 不然会GG
		lx1y2 = LCA(x1 , y2); ly1x2 = LCA(y1 , x2);
		if(lx1y1 == lx2y2) // 图1
		{
			if(lx1x2 == lx1y1 && ly1y2 == lx1y1)
				calc1(lx1y2 , ly1x2 , t1 + dis[x1] - dis[lx1y2] , t2 + dis[x2] - dis[ly1x2]); // 图1-1
			else
				calc0(lx1x2 , ly1y2 , t1 + dis[x1] - dis[lx1x2] , t2 + dis[x2] - dis[lx1x2]); // 1-2
			continue;
		}
		int lca = LCA(lx1y1 , lx2y2);
		if(lca != lx1y1) { puts("NO"); continue; } // 两条路径不相交
		if(LCA(x1 , lx2y2) == lx2y2) // 2
		{
			if(lx1x2 == lx2y2)
				calc1(lx1y2 , lx2y2 , t1 + dis[x1] - dis[lx1y2] , t2 + dis[x2] - dis[lx2y2]); //2-1
			else
				calc0(lx1x2 , lx2y2 , t1 + dis[x1] - dis[lx1x2] , t2 + dis[x2] - dis[lx1x2]); //2-2
			continue;
		}
		if(LCA(y1 , lx2y2) == lx2y2) // 3
		{
			if(ly1y2 == lx2y2)
				calc1(lx2y2 , ly1x2 , t1 + dis[x1] + dis[lx2y2] - dis[lca] * 2 , t2 + dis[x2] - dis[ly1x2]); // 3-1
			else
				calc0(lx2y2 , ly1y2 , t1 + dis[x1] + dis[lx2y2] - dis[lca] * 2 , t2 + dis[x2] - dis[lx2y2]); // 3-2
			continue;
		}
		puts("NO");
	}
	return ;
}

signed main()
{
	freopen("meet.in" , "r" , stdin);
	freopen("meet.out" , "w" , stdout);
	n = read(); Q = read();
	for(int i = 1 , u , v , c ; i < n ; ++i) u = read() , v = read() , c = read() , d[u]++ , d[v]++ , add(u , v , c , i) , add(v , u , c , i);
	if(n <= 100) solve1(); else solve2();
	fclose(stdin); fclose(stdout);
	return 0;
}
/*
8 6
1 2 3
1 3 1
1 4 2
2 5 5
2 6 1
5 7 2
5 8 4
5 3 2 7 4 2
8 6 1 1 7 6
4 5 1 4 5 10
7 8 3 3 4 5
6 7 6 5 1 2
2 1 10 8 3 3
*/