HDU - 1005 Number Sequence （矩阵快速幂）

A number sequence is defined as follows:

f(1) = 1, f(2) = 1, f(n) = (A * f(n - 1) + B * f(n - 2)) mod 7.

Given A, B, and n, you are to calculate the value of f(n).

InputThe input consists of multiple test cases. Each test case contains 3 integers A, B and n on a single line (1 <= A, B <= 1000, 1 <= n <= 100,000,000). Three zeros signal the end of input and this test case is not to be processed. 
OutputFor each test case, print the value of f(n) on a single line. 
Sample Input

1 1 3
1 2 10
0 0 0

Sample Output

2
5

原谅博主不会Markdown

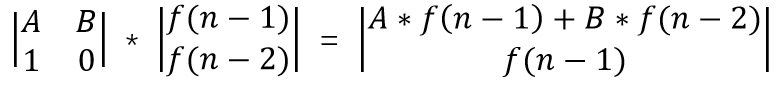
#include<iostream>
#include<algorithm>
#include<vector>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<ctime>
#define fuck(x) cout<<#x<<" = "<<x<<endl;
#define debug(a,i) cout<<#a<<"["<<i<<"] = "<<a[i]<<endl;
#define ls (t<<1)
#define rs ((t<<1)|1)
using namespace std;
typedef long long ll;
typedef unsigned long long ull;
const int maxn = ;
const int maxm = ;
const int inf = 2.1e9;
const ll Inf = ;
const int mod = ;
const double eps = 1e-;
const double pi = acos(-);

struct Matrix{
    int a[][];
};

Matrix mul(Matrix a,Matrix b){
    Matrix ans;
    for(int i=;i<=;i++){
        for(int j=;j<=;j++){
            ans.a[i][j]=;
            for(int k=;k<=;k++){
                ans.a[i][j]+=a.a[i][k]*b.a[k][j];
            }
            ans.a[i][j]%=mod;
        }
    }
    return ans;
}

Matrix q_pow(Matrix a,int b){
    Matrix ans ;
    ans.a[][]=ans.a[][]=;
    ans.a[][]=ans.a[][]=;
    while (b){
        if(b&){
            ans=mul(ans,a);
        }
        b>>=;
        a=mul(a,a);
    }
    return ans;
}

int main()
{
//    ios::sync_with_stdio(false);
//    freopen("in.txt","r",stdin);

    int A,B,n;

    while (scanf("%d%d%d",&A,&B,&n)!=EOF&&A&&B&&n){
        Matrix exa;
        if(n<=){printf("%d\n",);
            continue;
        }
        exa.a[][]=A;
        exa.a[][]=B;
        exa.a[][]=;
        exa.a[][]=;

        exa=q_pow(exa,n-);
        printf("%d\n",(exa.a[][]+exa.a[][])%);
    }
    return ;
}