题解【UVA10054】The Necklace

题目描述

输入格式

输出格式

题意简述

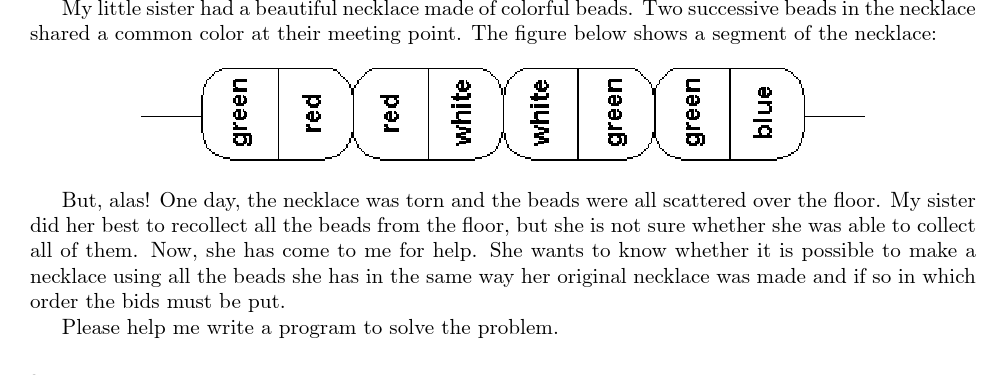
有一种由彩色珠子连接而成的项链。每个珠子的两半由不同颜色组成。如图所示，相邻两个珠子在接触的地方颜色相同。现在有一些零碎的珠子，需要确认它们是否可以复原成完整的项链。

输入格式：

输入第一行为测试数据组数 \(T\) 。每组数据的第一行是一个整数\(N (5 ≤ N ≤ 1000 )\)，表示珠子的个数。接下来的\(N\) 行每行包含两个整数，即珠子两半的颜色。颜色用\(1\)~\(50\)的整数来表示。

输出格式：

对于每组数据，输出测试数据编号和方案。如果无解，输出“some beads may be lost”。方案的格式和输入相同，也是一共\(N\) 行，每行用两个整数描述一个珠子（从左到右的顺序），其中第一个整数表示左半的颜色，第二个整数表示右半的颜色。根据题目规定，对于\(1≤i≤N-1\),第\(i\)行的第二个数必须等于第\(i+1\)行上的第一个数，且第\(N\)行的第二个数必须等于第一行的第一个数（因为项链是环形的）。如果有多解，输出任意一组即可。在相邻两组输出之间应有一个空行。

题解

这道题目是欧拉回路的经典题，不过需要通过建模才可以利用欧拉回路解题。

我们把每一种颜色都看成一个节点，把每一个珠子的两半都连一条有向边，那么这道题就变成了在一幅图中求解欧拉回路的经典题。

使用\(DFS\)进行欧拉回路的寻找，最后记得逆序输出。

通过本题，我们可以知道，数学建模在信息学上的作用很大，它是信息学中不可忽视的一个知识点。

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <cctype>//头文件准备

using namespace std;

inline int gi()
{
    int f = 1, x = 0; char c = getchar();
    while (c < '0' || c > '9') { if (c == '-') f = -1; c = getchar();}
    while (c >= '0' && c <= '9') { x = x * 10 + c - '0'; c = getchar();}
    return f * x;
}//快速读入

int n, m, g[53][53]/*存图的邻接矩阵*/, f[53]/*每个点的度*/, t/*数据组数*/, Case;

void GetEuler(int u)//欧拉回路
{
	for (int i = 1; i <= 50; i++)//枚举节点
	{
		if (g[i][u])//如果枚举的节点与当前节点有边连接
		{
			--g[i][u], --g[u][i];//两点之间减去一条边
			GetEuler(i);//继续遍历下一个节点
			printf("%d %d\n", i, u);//注意逆序输出
		}
	}
}

int main()
{
	t = gi();//输入数据组数
	while (t--)
	{
		memset(g, 0, sizeof(g));
		memset(f, 0, sizeof(f));//多组数据要初始化数组
		n = gi();//输入珠子的个数
		for (int i = 1; i <= n; i++)
		{
			int u = gi(), v = gi();//输入2个颜色
			++g[u][v], ++g[v][u]/*连边*/, ++f[u], ++f[v]/*加上度数*/;
		}
		printf("Case #%d\n", ++Case);//输出这是第几组数据
		int Sigma = 0;
		for (int i = 1; i <= 50; i++)
		{
			if (f[i] & 1) //如果当前节点的度数为奇数
			{
				Sigma = i;//标记为有节点的度数为奇数,即没有欧拉回路
				break;//直接退出循环
			}
		}
		if (Sigma) //如果没有欧拉回路
		{
			puts("some beads may be lost");//输出无解
		}
		else
		{
			for (int i = 1; i <= 50; i++)
			{
				GetEuler(i);//否则就输出欧拉回路的路径
			}
		}
		if (t) puts("");//每组数据后都需要空一行
	}
	return 0;//结束
}