kmp算法散记

1.

https://blog.csdn.net/abcjennifer/article/details/5794547

#include<bits/stdc++.h>
using namespace std;
char t[],p[];    //文本串t,模式串p
int next[];
//记录当前索引位置的前一个字符的相同前缀后缀的最长长度。

void getnext()//打表离线计算模式串p
{
    int len=strlen(p);

}

int KMP(char t[],char p[])
//统计模式串p在文本串s出现次数（允许重叠）
//文本串t，模式串p
{
    int ans=;        //统计值
    int i;            //在文本串s上移动进位的索引“指针”
    int n=strlen(t);//文本串t的长度
    int m=strlen(p);//模式串p的长度
    if(n== && m==)
    {
        if(t[]==p[]) return ;
        else return ;
    }
    getnext(p);        //获得模式串p的next数组
    int q=;        //在模式串q上移动进位的索引“指针”
    for(i=;i<n;i++)
    {
        while(q> && p[q]!=t[i]) q=next[q];
        if(p[q]==t[i]) q++;
        //某一位的字符匹配成功，继续匹配下一位
        if(q==m)//模式串在文本串中匹配成功
        {
            ans++;
            q=next[q];
        }
        //q总是被赋值给next[q]的，这是一种优化
    }
    return ans;
}

int main()
{
    int T;
    scanf("%d",&T);
    getchar();// 熟稔之！
    while(T--)
    {
        scanf("%s%s",p,t);
        printf("%d\n",KMP(t,p));
    }
    return ;
} 

2.

在重述 kmp算法的原理之前，BF  算法是绕不开的话题，也只有了解了BF算法，才能知道KMP算法的优势。

BF算法的原理是一位一位地比较，比较到失配位的时候，将（模式串）P串 向后移动一个单位，再从头一位一位地进行匹配。

int ViolentMatch(char* s,char* p)//文本串s,模式串p
{
	int slen=strlen(s);//文本串长度slen
	int plen=strlen(p);//模式串长度plen

	int i=0;
	int j=0;
	while(i<slen && j<plen)//匹配过程
	{
		if(s[i]==p[j])
		{
			i++;
			j++;
		}
		else
		{
			i=i-j+1;
			j=0;
		}
		//每次匹配失败时，i回溯，j被置为0.
	}
	if(j==plen) return i-j;
	//匹配成功，返回模式串p在文本串s中的位置，否则返回-1
	else 		return  -1;
}

3.

Knuth-Morris-Pratt 字符串查找算法，简称为 “KMP算法”，常用于在一个文本串S内查找一个模式串P 的出现位置，这个算法由Donald Knuth、Vaughan Pratt、James H. Morris三人于1977年联合发表，故取这3人的姓氏命名此算法。

next 数组各值的含义：代表当前字符之前的字符串中，有多大长度的相同前缀后缀。例如如果next [j] = k，代表j 之前的字符串中有最大长度为k 的相同前缀后缀。

在某个字符失配时，该字符对应的next 值会告诉你下一步匹配中，模式串P应该跳到哪个位置（跳到next [j] 的位置）。

　　如果next [j] 等于0或-1，则跳到模式串的开头字符；

　　若next [j] = k 且 k > 0，代表下次匹配跳到j 之前的某个字符，而不是跳到开头，且具体跳过了k 个字符。

int KmpSearch(char* s,char* p)//文本串s,模式串p
{
	int slen=strlen(s);//文本串s的长度 slen
	int plen=strlen(p);//模式串p的长度plen
	int i=0;		   //文本串p的指针
	int j=0; 		   //模式串s的指针
	while(i<slen && j<plen)	//匹配ing...
	{
		if(j==-1 || s[i]==p[j])
		{
			i++;
			j++;
		}
		else j=next[j];
	}
	if(j==plen) return i-j;
	else 		return -1;
}

4.

寻找前缀后缀最长公共元素长度

对于P = p0 p1 ...pj-1 pj，寻找模式串P中长度最大且相等的前缀和后缀。

如果存在p0 p1 ...pk-1 pk = pj- k pj-k+1...pj-1 pj，那么在包含pj的模式串中有最大长度为k+1的相同前缀后缀。

举个例子，如果给定的模式串为“abab”，那么它的各个子串的前缀后缀的公共元素的最大长度如下表格所示：

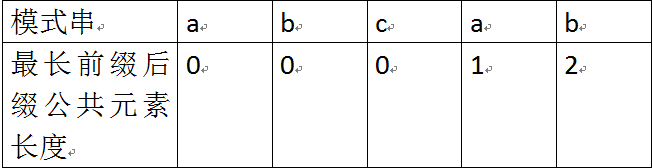
比如对于字符串aba来说，它有长度为1的相同前缀后缀a；而对于字符串abab来说，它有长度为2的相同前缀后缀ab。

next 数组考虑的是除当前字符外的也就是当前字符前的字符串的最长相同前缀后缀的长度，所以通过第1步骤求得各个子字符串的前缀后缀的公共元素的最大长度后，

只要稍作变形即可：将第一步骤中求得的值整体右移一位（-=1），然后初值赋为-1，如下表格所示：

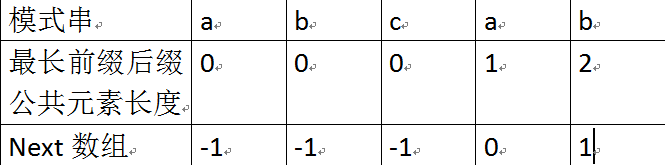
比如对于aba来说，第3个字符a之前的字符串ab中有长度为0的相同前缀后缀，所以第3个字符a对应的next值为0；

而对于abab来说，第4个字符b之前的字符串aba中有长度为1的相同前缀后缀a，所以第4个字符b对应的next值为1。

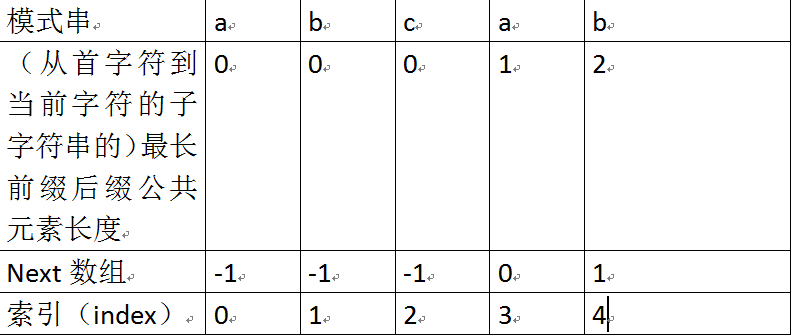
根据next数组进行匹配

匹配失配，j = next [j]，模式串向右移动（+=）的位数为：j - next[j]。

5.

接下来，咱们来写代码求下next 数组。

基于之前的理解，可知计算next 数组的方法可以采用递推：

　　　　如果对于值k，已有p0 p1, ..., pk-1 = pj-k pj-k+1, ..., pj-1，相当于next[j] = k。

　　　　此意味着什么呢？究其本质，next[j] = k 代表模式串P在index==j处的字符p[j] 之前的模式串子串中，有长度为k 的相同前缀和后缀。

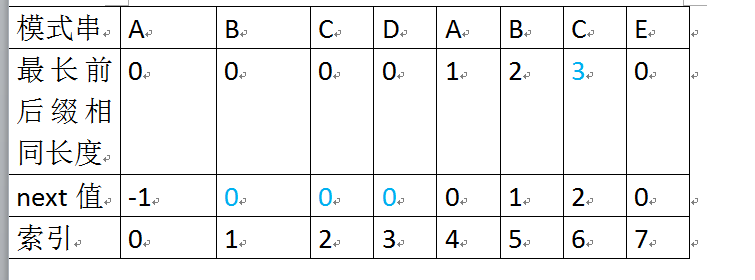
举个例子，如下图，根据模式串“ABCDABD”的next 数组可知失配位置的字符D对应的next 值为2，

代表字符D前有长度为2的相同前缀和后缀（这个相同的前缀后缀即为“AB”），失配后，模式串需要向右移动j - next [j] = 6 - 2 =4位。（光需要移动模式串P就好啦！）

向右移动4位后，模式串中的字符C继续跟文本串匹配。

下面的问题是：已知next [0, ..., j]，如何求出next [j + 1]呢？（如何由已知追求未知啦嘞！）

next [j] = k（相当于 “p0...pk-1”  ==  “pj-k...pj-1” ）

对于P的前j+1个序列字符：

6.

a beautiful picture:

可以通过递推求得next 数组，代码如下所示：

7.

KMP算法的匹配流程：

假设现在文本串S匹配到 i 位置，模式串P匹配到 j 位置：

　　　　如果（1）. j = -1，or （2）.当前字符匹配成功（即S[i] == P[j]）：都令i++，j++，继续匹配（match）下一个字符；

　　　　如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]。此举意味着失配时，模式串P相对于文本串S向右移动了j - next [j] 位。

（1）. 最开始匹配时

P[0]跟S[0]匹配失败，

所以执行“如果j != -1，且当前字符匹配失败（即S[i] != P[j]），则令 i 不变，j = next[j]”，所以j = -1，

故转而执行“如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++”，

得到i = 1，j = 0，即P[0]继续跟S[1]匹配。

P[0]跟S[1]又失配，j再次等于-1，i、j继续自增，从而P[0]跟S[2]匹配。

P[0]跟S[2]失配后，P[0]又跟S[3]匹配。，直到P[0]跟S[4]匹配成功，开始执行此条指令的后半段：

如果j = -1，或者当前字符匹配成功（即S[i] == P[j]），都令i++，j++：

（2）.

P[1]跟S[5]匹配成功，P[2]跟S[6]也匹配成功, ...，直到当匹配到P[6]处的字符D时失配（即S[10] != P[6]），由于P[6]处的D对应的next 值为2，

所以下一步用P[2]处的字符C继续跟S[10]匹配，相当于向右移动：j - next[j] = 6 - 2 =4 位。

（3）.

向右移动4位后，P[2]处的C再次失配，由于C对应的next值为0，所以下一步用P[0]处的字符继续跟S[10]匹配，相当于向右移动：j - next[j] = 2 - 0 = 2 位。

（4）.

移动两位之后，A 跟空格不匹配，模式串后移1 位。

（5）.

P[6]处的D再次失配，因为P[6]对应的next值为2，故下一步用P[2]继续跟文本串匹配，相当于模式串向右移动 j - next[j] = 6 - 2 = 4 位。

（6）.

匹配成功，过程结束。

当p[j] != s[i] 时，下次匹配必然是p[ next [j]] 跟s[i]匹配，如果p[j] = p[ next[j] ]，必然导致后一步匹配失败

（因为p[j]已经跟s[i]失配，然后你还用跟p[j]等同的值p[next[j]]去跟s[i]匹配，很显然，必然失配），所以不能允许p[j] = p[ next[j ]]。如果出现了p[j] = p[ next[j] ]咋办呢？

如果出现了，则需要再次递归，即令next[j] = next[ next[j] ]。

求next 数组的代码：

//求next数组的代码:
void GetNextval(char* p,int next[])
{
	int plen=strlen(p);
	next[0]=-1;
	int k=-1;//p[k]表示前缀
	int j=0;//p[j]表示后缀
	while(j<plen-1)//字符串p本身既不是其前缀也非其后缀.
	{
		if(k==-1 || p[k]==p[j])
		{
			k++;
			j++;
//Condition：k==-1 && p[j]!=p[k]
			if(p[j]!=p[k]) next[j]=k;
//Condition: p[j]==p[k]
			else 		   next[j]=next[k];
		}
		else k=next[k];
	}
} 

int KmpSearch(char* s,char* p)
{
	int slen=strlen(s);
	int plen=strlen(p);
	int i=0;
	int j=0;
	while(i<len && j<len)
	{
		if(j==-1||s[i]==p[j])
		{
			i++;
			j++;
		}
		else
		{
			j=next[j];
		}
	}
	if(j=plen) return i-j;
	else 	   return -1;
}