POJ3111 K Best —— 01分数规划 二分法

题目链接：http://poj.org/problem?id=3111

K Best

Time Limit: 8000MS		Memory Limit: 65536K
Total Submissions: 11380		Accepted: 2935
Case Time Limit: 2000MS		Special Judge

Description

Demy has n jewels. Each of her jewels has some value v_i and weight w_i.

Since her husband John got broke after recent financial crises, Demy has decided to sell some jewels. She has decided that she would keep k best jewels for herself. She decided to keep such jewels that their specific value is as large as possible. That is, denote the specific value of some set of jewels S = {i₁, i₂, …, i_k} as

.

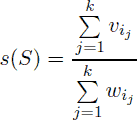Demy would like to select such k jewels that their specific value is maximal possible. Help her to do so.

Input

The first line of the input file contains n — the number of jewels Demy got, and k — the number of jewels she would like to keep (1 ≤ k ≤ n ≤ 100 000).

The following n lines contain two integer numbers each — v_i and w_i (0 ≤ v_i ≤ 10⁶, 1 ≤ w_i ≤ 10⁶, both the sum of all v_i and the sum of all w_i do not exceed 10⁷).

Output

Output k numbers — the numbers of jewels Demy must keep. If there are several solutions, output any one.

Sample Input

3 2
1 1
1 2
1 3

Sample Output

1 2

Source

Northeastern Europe 2005, Northern Subregion

 

 

 

 

题解：

 http://www.cnblogs.com/DOLFAMINGO/p/7563213.html

 

 

代码一：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const double EPS = 1e-;
 const int INF = 2e9;
 const LL LNF = 2e18;
 const int MAXN = 1e5+;

 struct node
 {
     double d;
     int a, b, id;
     bool operator<(const node x)const{
         return d>x.d;
     }
 }q[MAXN];
 int n, k;

 bool test(double L)
 {
     for(int i = ; i<=n; i++)
         q[i].d = 1.0*q[i].a - L*q[i].b;

     sort(q+, q++n);
     double sum = ;
     for(int i = ; i<=k; i++)   //取前k大的数
         sum += q[i].d;
     return sum>=;
 }

 int main()
 {
     while(scanf("%d%d", &n, &k)!=EOF)
     {
          //一次性把所有信息都录入结构体中，当排序时，即使打乱了顺序，仍然还记得初始下标。
         for(int i = ; i<=n; i++)
         {
             scanf("%d%d", &q[i].a, &q[i].b);
             q[i].id = i;
         }

         double l = , r = 1e7;
         while(l+EPS<=r)
         {
             double mid = (l+r)/;
             if(test(mid))
                 l = mid + EPS;
             else
                 r = mid - EPS;
         }

         for(int i = ; i<=k; i++)
             printf("%d ", q[i].id);
         printf("\n");
     }
 }

 

代码二：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const double EPS = 1e-;
 const int INF = 2e9;
 const LL LNF = 2e18;
 const int MAXN = 1e5+;

 struct node
 {
     double d;
     int id;
     bool operator<(const node x)const{
         return d>x.d;
     }
 }q[MAXN];

 int n, k;
 int a[MAXN], b[MAXN];

 bool test(double L)
 {
     for(int i = ; i<=n; i++)   //每一次q[i]都重新更新，与a[i],b[i]独立开来
     {
         q[i].id = i;
         q[i].d = 1.0*a[i] - L*b[i];
     }
     sort(q+, q++n);
     double sum = ;
     for(int i = ; i<=k; i++)
         sum += q[i].d;
     return sum>=;
 }

 int main()
 {
     while(scanf("%d%d", &n, &k)!=EOF)
     {
         for(int i = ; i<=n; i++)
             scanf("%d%d", &a[i], &b[i]);

         double l = , r = 1e7;
         while(l+EPS<=r)
         {
             double mid = (l+r)/;
             if(test(mid))
                 l = mid + EPS;
             else
                 r = mid - EPS;
         }

         for(int i = ; i<=k; i++)
             printf("%d ", q[i].id);
         printf("\n");
     }
 }

错误代码：

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 #include <cmath>
 #include <algorithm>
 #include <vector>
 #include <queue>
 #include <stack>
 #include <map>
 #include <string>
 #include <set>
 #define ms(a,b) memset((a),(b),sizeof((a)))
 using namespace std;
 typedef long long LL;
 const double EPS = 1e-;
 const int INF = 2e9;
 const LL LNF = 2e18;
 const int MAXN = 1e5+;

 struct node
 {
     double d;
     int id;
     bool operator<(const node x)const{
         return d>x.d;
     }
 }q[MAXN];

 int n, k;
 int a[MAXN], b[MAXN], ans[MAXN];

 bool test(double L)
 {
     //经过一次排序后，q[i].id不再等于i，所以出错。应该同时更新q[i].id
     for(int i = ; i<=n; i++)
         q[i].d = 1.0*a[i] - L*b[i];

     sort(q+, q++n);
     double sum = ;
     for(int i = ; i<=k; i++)
         sum += q[i].d;
     return sum>;
 }

 int main()
 {
     while(scanf("%d%d", &n, &k)!=EOF)
     {
         for(int i = ; i<=n; i++)
         {
             scanf("%d%d", &a[i], &b[i]);
             q[i].id = i;
         }

         double l = , r = 1e7;
         while(l+EPS<=r)
         {
             double mid = (l+r)/;
             if(test(mid))
                 l = mid + EPS;
             else
                 r = mid - EPS;
         }

         for(int i = ; i<=k; i++)
             printf("%d ", q[i].id);
         printf("\n");
     }
 }