luogu P3959(2017noipTG D2T2

luogu P3959(2017noipTG D2T2

不知道为什么,这两天见了好多伪装成图的dp题,这道也是.

最短路只有40分,实际上可以从数据范围n<=12看出来是状压dp.

solution:

题意就是找到一种连接方法,使这些点在同一连通块中且代价最小.

因为n<=12,所以dfs+状压dp去做.

具体操作见注释.

AC码:

#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;

int n,m,cnt,out[15],k,ans=1e9+7,E[15][15],dp[15][15][1<<15];
//dp[x][d][s] 点x在集合s中深度为d时的最小总代价
//目标状态为cnt==(1<<n)-1
//out[i]为层数 

void work(int x,int sum,int deep)
{
	//转移方程为dp[x][deep][1<<(x-1)]=min(dp[x][deep][1<<(x-1)],sum+out[i]*E[i][j])
	//sum为上一层dp时的最优解,deep为层数,x为当前的集合
	if(sum>=ans) return ;//剪 枝
	if(x==cnt)
	{
		ans=sum;
		return ;
	}
	for(int i=1;i<=n;i++)
	{
		if(!(1<<(i-1)&x)) continue ;
		for(int j=1;j<=n;j++)
		{
			if(!((1<<(j-1))&x)&&E[i][j]<1e9+7)
			{
				if(dp[j][deep+1][1<<(j-1)|x]<=sum+out[i]*E[i][j]) continue;
				dp[j][deep+1][1<<(j-1)|x]=sum+out[i]*E[i][j];
				out[j]=out[i]+1;
				work(1<<(j-1)|x,dp[j][deep+1][1<<(j-1)|x],deep+1);
			}
		}
	}
}

int main()
{
	scanf("%d%d",&n,&m);
	cnt=(1<<n)-1;
	memset(E,0x3f,sizeof(E));
	while(m--)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		E[u][v]=E[v][u]=min(E[u][v],w);
//		add(u,v,w);add(v,u,w);
//		in[u]++;in[v]++;
//		out[u]++;out[v]++;
//		if(out[u]>out[v]&&out[u]>out[maxu]) maxu=u;
//		if(out[v]>out[u]&&out[v]>out[maxu]) maxu=v;
//		maxout=max(maxout,max(out[u],out[v]));
	}
	for(int i=1;i<=n;i++)
	{
		memset(out,0,sizeof(out));
		memset(dp,0x3f,sizeof(dp));
		out[i]=1;
		//初始化
		work(1<<(i-1),0,0);
	}
	printf("%d\n",ans);
	return 0;
 }

---

状压dp复习:

个人认为状压最重要的就是位运算,通常情况下状压都是采用二进制压缩的(听说有三进制的,但是太菜不会)

一张关于位运算操作的图(网上找的

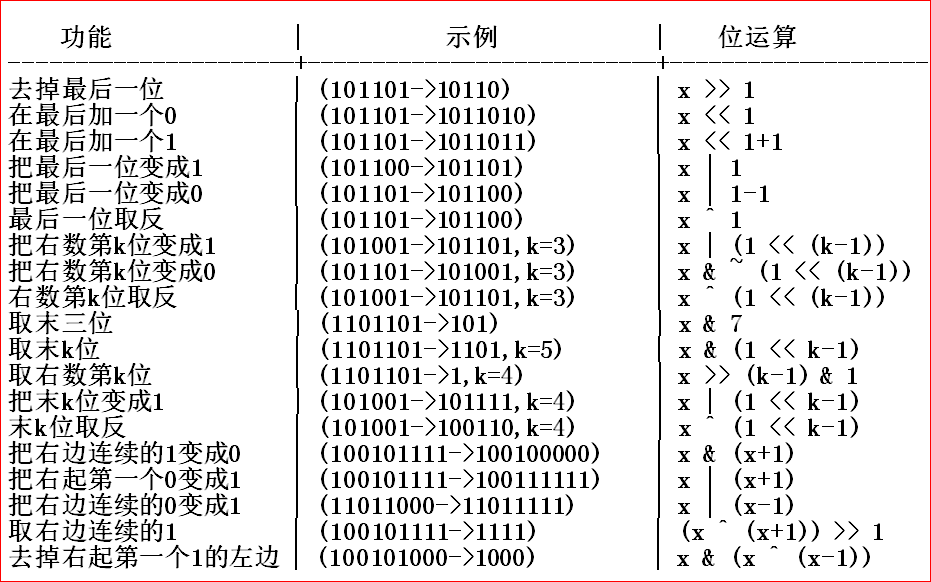
十分感谢 ___new2zy___dalao的博客,这是链接.

然后就想说一下如何选择状压dp的问题.(个人经验

通常情况下n不会超过64,一般对于每个点(步骤)存在两种情况,如:选or不选,输or赢.

其余的性质和普通dp一样(无后效性,最优,阶段)