经典网络流题目模板（P3376 + P2756 + P3381 : 最大流 + 二分图匹配 + 最小费用最大流）
题目来源
最大流
最大流问题是网络流的经典类型之一，用处广泛，个人认为网络流问题最具特点的操作就是建反向边，这样相当于给了反悔的机会，不断地求增广路的，最终得到最大流
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e6 + ;
const int Max = 1e5 + ; struct Edge {
int to, next, flow; //flow记录这条边当前的边残量
}edge[Max << ]; int n, m, s, t;
int head[Max], tot;
bool vis[Max]; void init()
{
memset(head, -, sizeof(head));tot = ;
} void add(int u, int v, int flow)
{
edge[tot].to = v;
edge[tot].flow = flow;
edge[tot].next = head[u];
head[u] = tot++;
} //向图中增加一条容量为exp的边（增广路）
int dfs(int u,int exp)
{
if (u == t) return exp; //到达汇点，当前水量全部注入
vis[u] = true; //表示已经到了过了
for(int i = head[u] ; i != - ;i = edge[i].next)
{
int v = edge[i].to;
if(!vis[v] && edge[i].flow > )
{
int flow = dfs(v, min(exp, edge[i].flow));
if(flow > ) //形成了增广路
{
edge[i].flow -= flow;
edge[i ^ ].flow += flow;
return flow;
} } }
return ; //无法形成增广路的情况
} //求最大流
int max_flow()
{
int flow = ;
while(true)
{
memset(vis, , sizeof(vis));
int part_flow = dfs(s, inf);
if (part_flow == ) return flow;
flow += part_flow;
}
} int main()
{
#ifdef LOCAL
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
while (scanf("%d%d%d%d", &n, &m, &s, &t) != EOF)
{
init();
for (int i = , u, v, flow;i <= m; i++)
{
scanf("%d%d%d", &u, &v, &flow);
add(u, v, flow);add(v, u, );
}
printf("%d\n", max_flow());
} return ;
}
最简单算法-Ford-Fulkerson
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) "["<<x<<","<<y<<"]"
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e6 + ;
const int Max = 1e5 + ; struct Edge {
int to, next, flow; //flow记录这条边当前的边残量
}edge[Max << ]; int n, m, s, t;
int head[Max], tot;
int dis[Max]; void init()
{
memset(head, -, sizeof(head));tot = ;
} void add(int u, int v, int flow)
{
edge[tot].to = v;
edge[tot].flow = flow;
edge[tot].next = head[u];
head[u] = tot++;
} bool bfs() //判断图是否连通
{
queue<int>q;
memset(dis, -, sizeof(dis));
dis[s] = ;
q.push(s);
while (!q.empty())
{
int u = q.front();q.pop();
for (int i = head[u]; i != -; i = edge[i].next)
{
int v = edge[i].to;
if (dis[v] == - && edge[i].flow > ) //可以借助边i到达新的结点
{
dis[v] = dis[u] + ; //求顶点到源点的距离编号
q.push(v);
}
}
}
return dis[t] != -; //确认是否连通
} int dfs(int u, int flow_in)
{
if (u == t) return flow_in;
int flow_out = ; //记录这一点实际流出的流量
for (int i = head[u]; i != -;i = edge[i].next)
{
int v = edge[i].to;
if (dis[v] == dis[u] + && edge[i].flow > )
{
int flow_part = dfs(v, min(flow_in, edge[i].flow));
if (flow_part == )continue; //无法形成增广路
flow_in -= flow_part; //流出了一部分，剩余可分配流入就减少了
flow_out += flow_part; //记录这一点最大的流出 edge[i].flow -= flow_part;
edge[i ^ ].flow += flow_part; //减少增广路上边的容量，增加其反向边的容量
if (flow_in == )
break;
}
}
return flow_out;
} int max_flow()
{
int sum = ;
while (bfs())
{
sum += dfs(s, inf);
}
return sum;
} int main() {
#ifdef LOCAL
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
while (scanf("%d%d%d%d", &n, &m, &s, &t) != EOF)
{
init();
for (int i = , u, v, flow;i <= m; i++)
{
scanf("%d%d%d", &u, &v, &flow);
add(u, v, flow);add(v, u, );
} printf("%d\n", max_flow());
} return ;
}
常用且高效的算法-Dinic
二分图匹配
要解决这类问题，我们需要先了解什么是二分图？
二分图：一个图中的所有顶点可以分为两个集合 V,K ,其实两个集合内部的点彼此之间无边，如下图所示：（蓝色的点和红色的点分属于两个集合V,K)
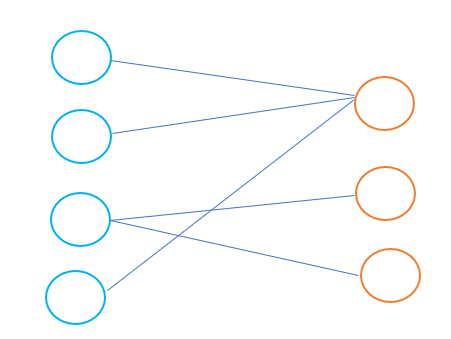
然后我们回到这个题目上来，这个题目求的是最大可出战人数，实际上就是在二分图中找到两个集合中的最大匹配数，这类问题我们称之为二分图最大匹配数问题
属于网络流经典题目之一，下面说明一下建图的过程
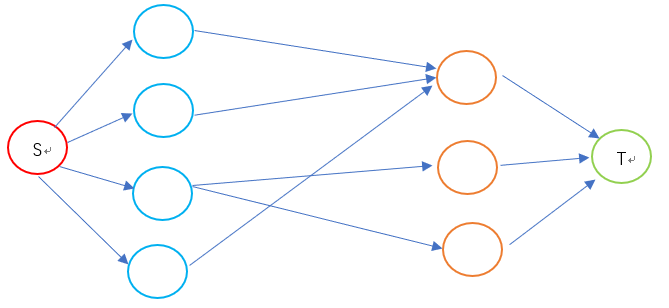
1）由源点向集合V中每个点建一条容量为1的边
2）对于V，K集合之间存在的边e，v 为V中的点,k为K中的点，我们建一条容量为1的边，方向为 v --> k
3）由K中每个点向汇点建一条容量为1的边
当我们将图建好了后，我们求这个图的最大流，这个最大流即为二分图最大匹配数，下面展示一下建成的图：(S代表源点，T代表汇点，蓝色的边代表容量为1的边）
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e6 + ;
const int Max = 1e6 + ; struct Edge
{
int to, next, flow;
}edge[Max << ];; int n, m, a, b, s, t;
int head[Max], tot;
int dis[Max];
int ans;
bool vis[Max]; void init()
{
memset(head, -, sizeof(head));tot = ;
ans = ;
} void add(int u, int v, int flow)
{
edge[tot].to = v;
edge[tot].flow = flow;
edge[tot].next = head[u];
head[u] = tot++;
} bool bfs()
{
memset(dis, -, sizeof(dis));
dis[s] = ;
queue<int>q;
q.push(s);
while (!q.empty())
{
int u = q.front();q.pop();
for (int i = head[u]; i != -;i = edge[i].next)
{
int v = edge[i].to;
if (dis[v] == - && edge[i].flow > )
{
dis[v] = dis[u] + ;
if (v == t) return true;
q.push(v);
}
}
}
return false;
} int dfs(int u, int flow_in)
{
if (u == t) return flow_in;
int flow_out = ;
for (int i = head[u]; i != -;i = edge[i].next)
{
int v = edge[i].to;
if (dis[v] == dis[u] + && edge[i].flow > )
{
int flow_part = dfs(v, min(flow_in, edge[i].flow));
if (flow_part == ) continue;
flow_in -= flow_part;
flow_out += flow_part;
edge[i].flow -= flow_part;
edge[i ^ ].flow += flow_part;
if (flow_in == )break;
}
}
return flow_out;
} int max_val()
{
int sum = ;
while (bfs())
{
sum += dfs(s, inf);
}
return sum;
} int main()
{
#ifdef LOCAL
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
while (scanf("%d%d", &m, &n) != EOF)
{
init();
s = , t = n + ;
for (int i = ;i <= m;i++)
{
add(s, i, );add(i, s, ); //由源点向外籍飞行员建边
}
for (int i = m + ; i <= n;i++)
{
add(i, t, );add(t, i, );
}
while (scanf("%d%d", &a, &b) != EOF && a != - && b != -)
{
add(a, b, );add(b, a, );
}
printf("%d\n", max_val());
for (int u = ;u <= m;u++)
{
for (int i = head[u]; i != -;i = edge[i].next)
{
if (edge[i].flow == && edge[i].to != s && edge[i].to != t)
{
printf("%d %d\n", u, edge[i].to);
}
}
}
}
return ;
}
飞行员配对方案-Dinic
最小费用最大流
这类题目相比于最大流问题新增了每天边单位流量的价格，问在最大流的情况下求出最小的费用。
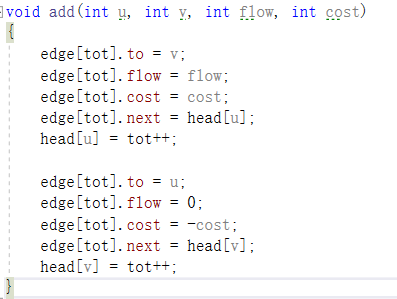
这类题目和最大流很想，不过也有不小区别，对于这类问题，我们为每条边建的反边的价格是每天边的相反数，如图
然后我们的算法也不再是Dinic算法了，而是用spfa或者dijkstra
#pragma GCC optimize(2)
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e9 + ;
const int Max = 5e3 + ; struct Edge
{
int to, rev; //rev记录反向边
int flow, cost;;
}; int n, m, k;
vector<Edge>edge[Max << ];
int h[Max]; //每个结点的势
int dis[Max];
int pre_node[Max], pre_edge[Max]; //前驱结点和对应边 void add(int u, int v, int flow, int cost)
{
edge[u].push_back({ v,(int)edge[v].size(),flow,cost }); edge[v].push_back({ u,(int)edge[u].size() - ,,-cost });
} void min_cost_flow(int s, int t, int& min_cost, int& max_flow)
{
fill(h + , h + + n, );
min_cost = max_flow = ;
int tot = inf; //源点流量无限
while (tot > )
{
priority_queue<pair<int, int>, vector<pair<int, int> >, greater<pair<int, int> > >q;
memset(dis, inf, sizeof(dis));
dis[s] = ;q.push({ ,s });
while (!q.empty())
{
int u = q.top().second;
int dist = q.top().first;
q.pop();
if (dis[u] < dist)continue; //当前的距离不是最近距离
for (int i = ;i < edge[u].size(); i++)
{
Edge &e = edge[u][i];
if (edge[u][i].flow > && dis[e.to] > dis[u] + e.cost + h[u] - h[e.to])
{
dis[e.to] = dis[u] +e.cost + h[u] - h[e.to];
pre_node[e.to] = u;
pre_edge[e.to] = i;
q.push({ dis[e.to],e.to });
}
}
}
if (dis[t] == inf)break; //无法增广了，就是找到答案了
for (int i = ;i <= n;i++) h[i] += dis[i];
int flow = tot; //求这一增广路径的流量
for (int i = t; i != s; i = pre_node[i])
flow = min(flow, edge[pre_node[i]][pre_edge[i]].flow);
for (int i = t; i != s; i = pre_node[i])
{
Edge& e = edge[pre_node[i]][pre_edge[i]];
e.flow -= flow;
edge[i][e.rev].flow += flow;
}
tot -= flow;
max_flow += flow;
min_cost += flow * h[t];
}
} int main()
{
#ifdef LOCAL
//freopen("input.txt", "r", stdin);
//freopen("output.txt", "w", stdout);
#endif
int s, t;
while (scanf("%d%d%d%d", &n, &m, &s, &t) != EOF)
{
for (int i = , u, v, flow, cost;i <= m;i++)
{
scanf("%d%d%d%d", &u, &v, &flow, &cost);
add(u, v, flow, cost);
}
int min_cost, max_flow;
min_cost_flow(s, t, min_cost, max_flow);
printf("%d %d\n", max_flow, min_cost);
}
return ;
}
无负环图中可用的算法-dijkstra（这里给出的是可以适用于有负环的
#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<queue>
#include<string>
#include<fstream>
#include<vector>
#include<stack>
#include <map>
#include <iomanip>
#define bug cout << "**********" << endl
#define show(x,y) cout<<"["<<x<<","<<y<<"] "
//#define LOCAL = 1;
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const ll mod = 1e9 + ;
const int Max = 1e5 + ; struct Edge
{
int to, next;
int flow, cost;
}edge[Max << ]; int n, m, s, t;
int head[Max], tot;
int dis[Max];
int pre[Max]; //记录增广路径此点的前一天边
bool vis[Max]; void init()
{
memset(head, -, sizeof(head));tot = ;
} void add(int u, int v, int flow, int cost)
{
edge[tot].to = v;
edge[tot].flow = flow;
edge[tot].cost = cost;
edge[tot].next = head[u];
head[u] = tot++; edge[tot].to = u;
edge[tot].flow = ;
edge[tot].cost = -cost;
edge[tot].next = head[v];
head[v] = tot++;
} bool spfa(int s, int t)
{
memset(dis, inf, sizeof(dis));
memset(vis, , sizeof(vis));
memset(pre, -, sizeof(pre)); queue<int>q;
q.push(s);dis[s] = ;vis[s] = true; while (!q.empty())
{
int u = q.front();q.pop();
vis[u] = false;
for (int i = head[u]; i != -; i = edge[i].next)
{
int v = edge[i].to;
if (edge[i].flow > && dis[v] > dis[u] + edge[i].cost)
{
dis[v] = dis[u] + edge[i].cost;
pre[v] = i; if (!vis[v])
{
vis[v] = true;q.push(v);
}
}
}
}
return pre[t] != -;
} void min_cost_max_flow(int s, int t, int& max_flow, int& min_cost)
{
max_flow = ;
min_cost = ;
while (spfa(s, t))
{
int flow = inf;
for (int i = pre[t]; i != -; i = pre[edge[i ^ ].to]) //沿增广路回溯edge[i^1]即为其反边
{
flow = min(flow, edge[i].flow);
}
for (int i = pre[t]; i != -; i = pre[edge[i ^ ].to])
{
edge[i].flow -= flow;
edge[i ^ ].flow += flow;
min_cost += flow * edge[i].cost;
}
max_flow += flow;
}
} int main()
{
#ifdef LOCAL
freopen("input.txt", "r", stdin);
freopen("output.txt", "w", stdout);
#endif
while (scanf("%d%d%d%d", &n, &m, &s, &t) != EOF)
{
init();
for (int i = , u, v, flow, cost;i <= m;i++)
{
scanf("%d%d%d%d", &u, &v, &flow, &cost);
add(u, v, flow, cost);
}
int max_flow = , min_cost = ;
min_cost_max_flow(s, t, max_flow, min_cost);
printf("%d %d\n", max_flow, min_cost);
}
return ;
}
常用且比较高效的算法-spfa
经典网络流题目模板（P3376 + P2756 + P3381 : 最大流 + 二分图匹配 + 最小费用最大流）的更多相关文章
- Doctor NiGONiGO’s multi-core CPU（最小费用最大流模板）
题目链接:http://acm.nyist.net/JudgeOnline/problem.php?pid=693 题意:有一个 k 核的处理器和 n 个工作,全部的工作都须要在一个核上处理一个单位的 ...
- P3381 【模板】最小费用最大流
P3381 [模板]最小费用最大流 题目描述 如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用. 输入输出格式 输入格式: 第一行 ...
- 洛谷P3381 最小费用最大流模板
https://www.luogu.org/problem/P3381 题目描述 如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用 ...
- P3381 【模板】最小费用最大流（MCMF）
P3381 [模板]最小费用最大流 题目描述 如题,给出一个网络图,以及其源点和汇点,每条边已知其最大流量和单位流量费用,求出其网络最大流和在最大流情况下的最小费用. 输入格式 第一行包含四个正整数N ...
- Luogu P3381 (模板题) 最小费用最大流
<题目链接> 题目大意: 给定一张图,给定条边的容量和单位流量费用,并且给定源点和汇点.问你从源点到汇点的最带流和在流量最大的情况下的最小费用. 解题分析: 最小费用最大流果题. 下面的是 ...
- P3381 【模板】最小费用最大流 题解
CSDN同步 原题链接 前置知识: 从三种算法剖析网络流本质 简要题意: 给定网络图,求图的最大流,以及流量为最大流时的最小费用. 现在假设你们看了那篇网络流博客之后,所有人都会了 \(\text{E ...
- 【网络流#2】hdu 1533 - 最小费用最大流模板题
最小费用最大流,即MCMF(Minimum Cost Maximum Flow)问题 嗯~第一次写费用流题... 这道就是费用流的模板题,找不到更裸的题了 建图:每个m(Man)作为源点,每个H(Ho ...
- 洛谷P3381 - 【模板】最小费用最大流
原题链接 题意简述 模板题啦~ 题解 每次都以费用作为边权求一下最短路,然后沿着最短路增广. Code //[模板]最小费用最大流 #include <cstdio> #include & ...
- poj2135最小费用最大流经典模板题
Farm Tour Time Limit: 1000MS Memory Limit: 65536K Total Submissions: 13509 Accepted: 5125 Descri ...
随机推荐
- Taro 遇到的坑
1.createSelectorQuery无法获取节点宽高 业务场景: 列表需要在最后一页底部显示 ‘我是有底线的~’ 提示,但是如果数据只有一页且不占满屏幕的话,就不显示.需要判断 ‘我是有底线的~ ...
- 0.JQuery学习
jQuery 教程 jQuery 是一个 JavaScript 库. jQuery 极大地简化了 JavaScript 编程. jQuery 简介 jQuery 库可以通过一行简单的标记被添加到网页中 ...
- TCP 之 TCP_NEW_SYN_RECV状态
概述 以前的TCP请求控制块没有独立的状态,而是依赖于他们的父控制块的状态,也就是TCP_LISTEN状态,现在要把请求控制块加入到全局的ehash中,所以需要一个状态,而TCP_SYN_RECV状态 ...
- TCP发送窗口更新tcp_ack_update_window
在tcp_ack接收ACK处理函数中,如果确认当前走慢速路径,那么会调用tcp_ack_update_window函数检查窗口是否需要更新并更新之,并且更新未确认数据的位置,即更新窗口左边沿: sta ...
- State Threads之co-routine的创建和stack的管理
1. 综述 协程库 State Threads Library 是一个基于 setjmp/longjmp 实现的 C 语言版用户线程库或协程库(user level thread). 基本协程例子: ...
- JSP——常用配置-获取项目跟路径
将该内容放入一个空白的JSP文件中,保存为basepath.jsp,然后在需要引用的JSP文件中使用include标签引用. <% String path = request.getContex ...
- Mac 下 Android Studio 连 夜神模拟器 调试
1.运行夜神模拟器(自行搜索下载) 2.进入资源目录 cd /Applications/Nox\ App\ Player.app/Contents/MacOS 3.执行命令连接 adb connect ...
- Oracle 性能之 Enq: CF - contention
Oracle 性能之 Enq: CF - contention Table of Contents 1. 原因 2. 解决问题 2.1. 针对持有锁进程类型处理 2.1.1. 查看持有锁会话的进程类型 ...
- 2019-8-13未命名文件 sdfsdfsdfsdfsdfsdf
2019-8-13未命名文件 sdfsdfsdfsdfsdfsdf 新建模板小书匠 欢迎使用 小书匠(xiaoshujiang)编辑器,您可以通过 小书匠主按钮>模板 里的模板管理来改变新建文章 ...
- git介绍以及常用命令操作
一.git与SVN的对比[面试] ①git是分布式的,SVN是集中式的(最核心) ②git是每个历史版本都存储完整的文件,便于恢复,SVN是存储差异文件,历史版本不可恢复(核心) ③git可离线完成大 ...